在海外科技网站，现在常可以看到冠以“贝叶斯”名字的术语，如，贝叶斯网络、贝叶斯机器学习、贝叶斯深度学习、贝叶斯人工智能、贝叶斯主义、贝叶斯大脑、贝叶斯计量经济学、贝叶斯医学诊断、贝叶斯信息准则、贝叶斯控制器融合、贝叶斯模型、贝叶斯分类器...。这些均基于贝叶斯定理——18世纪一位名叫托马斯·贝叶斯的牧师提出的数学公式。这个曾经鲜为人知的数学公式，现在正被用于环境保护、气象预测、疾病诊断、疫情预测、资源勘探、城市管理、经济金融，以及智能手机和无人驾驶汽车等。这项技术表明数学公式可以帮助改进人类专家的决策过程。

这篇博文将介绍贝叶斯定理的基本概念，讨论贝叶斯推理两例，以及涉及贝叶斯推理的争议。

贝叶斯定理

在概率论与数理统计中，贝叶斯定理(也称为贝叶斯规则)是一个数学公式，用于确定事件的条件概率。这个定理是英国非传统神学家和数学家托马斯·贝叶斯（Thomas Bayes，1702-1761）提出的。它是被称为贝叶斯推理的统计推断方法的基础。

除了统计学之外，贝叶斯定理被用于各种学科，医学和药理学是最著名的例子。另一个例子是贝叶斯方法在很大程度上促进了天气预报的改进。新数据不断更新旧模型，我们预测天气的能力也随之增加。此外，该定理被应用于不同的金融领域，例如，风险评估、欺诈检测、信用评分，以及投资策略优化——预测投资成功的概率。

考虑事件A和B的条件概率公式：

P(A & B) = P(A|B)P(B)

P(A & B) = P(B|A)P(A)

通过结合两个公式，我们有

P(A|B)P(B) = P(B|A)P(A)

由此，得到贝叶斯定理的公式：

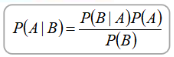
这建立了P(A|B)和P(B|A)之间的关系。

利用贝叶斯公式进行推理

20世纪80年代开始悄然兴起的贝叶斯主义，其思想包括：其一，认识到不确定性最好用概率来表达；其二，学习和归纳推理可以成功地用条件概率和贝叶斯定理来建模。

贝叶斯推理是一种统计推断方法，在这种方法中，随着更多的证据或信息变得可用，贝叶斯定理用于更新假设的概率。这种方法允许将先前的知识或信念结合到分析中，使其成为在不确定性下进行决策和推理的有力工具。

利用贝叶斯公式进行推理，首先要把问题表述成一个或多个假设。假设H是一个真假未知的命题。例如，假设可能是某人患有冠状病毒肺炎。如果随机选择一个人，那么这个问题的答案将是未知的。但专家们会对这种可能性有一个初步的想法——称之为先验概率，它是在没有任何进一步信息的情况下，对事件发生的可能性的度量。概率用0到1之间的数值表示事件发生的可能性。对先验概率的良好估计，可以从专家那里获得，也可以从统计平均值中估计出它的值。我们用P(H)来表示H的先验概率。

下一步是使用证据来更新H的先验概率。通常用E表示证据，写作P(E)。通过利用当前观察的证据，结合假设的先验概率，计算出反映当前情况的更新概率——即后验概率。我们将假设H为真时证据E为真的概率写成P(E|H)。

贝叶斯公式用于在收到新证据时，更新假设的概率。如果新的证据与假设一致，那么假设的概率增加，否则，它可能减少。用数学符号书写的贝叶斯公式是:

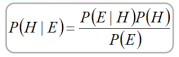
其中:

p(H| E)–在事件E发生情况下，事件H发生的概率。

P(E| H)–在事件H发生情况下，事件E发生的概率。

p(H)–事件H的概率。

p(E)–事件E的概率。

我们将P(E| H)、P(H)、P(E)值代入公式右边，可以求得P(H|E)的更新值。

贝叶斯定理的一个特例是事件H是一个二元变量。在这种情况下，该定理用以下方式表示:

其中:

P(E| H^-) —— 在事件H^-发生情况下，事件E发生的概率。

P(E| H⁺)——在事件H⁺发生情况下，事件E发生的概率。

在上面的特例中，事件H^-和H⁺是事件H的互斥结果。

贝叶斯推理两例

下面介绍的两个应用贝叶斯推理的著名示例，被许多人讨论过。

例一. ELISA检查阳性者患艾滋病毒的概率（参考资料[1]）

[ 问题陈述 ]

成年男性人口中艾滋病患病率约为1%。血液含有艾滋病毒（HIV）的“患者”，有98%的ELISA HIV检查会呈阳性结果。血液不含有艾滋病毒的“非患者”，有95%的ELISA HIV检查会呈阴性结果。老刘刚得到ELISA HIV检查呈阳性结果，想知道老刘患艾滋病毒的概率。

[ 解 ]

让我们用H表示患艾滋病，用T表示ELISA检查呈阳性。问题陈述告诉我们：

P(H)=0.01  P(T|H)=0.98  P(not T|not H)=0.95.

根据补集规则，我们可以推断

P(not H)=0.99  P(not T|H)=0.02  P(T|not H)=0.05.

所有这些数据如下表所示：

我们已经知道事件老刘检查呈阳性，而我们想知道老刘患病的概率，这要用贝叶斯定理了：

这里，我们还不知道P(T)，问题陈述中没有明确给出总体检查呈阳性的概率。但是，我们可以应用全概率法则计算：

检查呈阳性率=成年男性患病率×患病者检查阳性率

                 +成年男性未患病率×非患病者检查阳性率

P(T)=P(H)P(T|H)+P(not H)P(T|not H)=0.01×0.98+0.99×0.05.

最后，我们将这个结果代入贝叶斯定理。

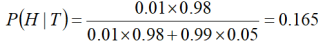
所以，虽然老刘ELISA HIV检测呈阳性，他实际患HIV的概率只有16.5％！

低概率一开始可能让人感到惊讶。正如Dennis Sun指出的，如果我们从几何角度来考虑这个问题，这就说得通了。下面的图将成年男性根据其艾滋病毒感染状态和检查结果进行了划分。阴影区域代表所有检查呈阳性的人。实际上患有艾滋病毒的人只占所有检查呈阳性的人的一小部分，因为没有患病的人太多了，导致假阳性超过了真阳性。

例二. 蒙蒂霍尔问题（参考资料 [2]）

蒙蒂霍尔问题（Monty Hall problem），也称“三门问题”，是一个违反直觉的统计谜题，源于自美国的电视游戏节目Let's Make a Deal。问题的名字来自该节目的主持人蒙蒂·霍尔（Monty Hall）。

[ 问题陈述 ]

你在参加一个游戏节目，被要求在三扇门之中做出选择。在这三扇门中，有一扇门的后面是汽车，另外两扇门的后面是山羊。你选择了一扇门。主持人蒙蒂挑选了另一扇门，蒙蒂知道这扇门后面是一只山羊，然后打开门，给你看那只山羊。蒙蒂然后问你“是否愿意将你选择的门，切换到剩下的另一扇门？”。假设你更喜欢一辆汽车而不是一只山羊，你选择换门还是不换门？这就是蒙蒂霍尔问题。

答案是改变选择会让你赢的概率是坚持原来选择的两倍。这个结果对很多人来说似乎是违反直觉的。蒙蒂霍尔问题曾经让拥有博士学位的数学家感到过尴尬。当时被称为“世界上最聪明的人”的玛丽莲·沃斯·萨凡特，有一个名为“问问玛丽莲”的专栏，她说“换”是更好的策略。一些教授给她写信证明“换”不会有帮助，他们还在《游行》杂志的一个专栏中“纠正”玛丽莲。

“蒙蒂霍尔问题的变种”是指如果蒙蒂真正随机地打开一扇门（里面可能是羊，也可能是车），碰巧在这个门的后面是一只羊，蒙蒂问你换不换门？在这种情况下，答案是“不换门”和“换门”中奖概率是一样的。

蒙蒂霍尔问题及其变种，有两个方面是许多人难以理解的：第一，在蒙蒂霍尔问题中，为什么主持人打开一个门后，为什么“换门”有三分之二的胜算而坚持原来选择“不换门”只有三分之一的胜算？第二，在蒙蒂霍尔问题的变种中，为什么如果蒙蒂真正随机地打开了一扇门，并且碰巧展示了一只山羊，这时选择“不换门”和“换门”的中奖的概率是50%-50%？下面在回答这两个问题时候用到了贝叶斯定理。

[ 蒙蒂霍尔问题的解 ]

一种看待解决方案的方法是明确列出所有可能的结果，并计算如果你留在原来选择的门（不换门）或者换门时，你得到汽车的频率。不失一般性，假设你最初选择门1，那么可能的结果可以在下表中看到：

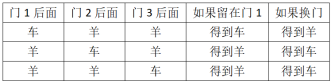
可以看出，在最初选择的门1后面是汽车的情况下（概率1/3），其它两扇门后面是羊,蒙蒂打开的一扇门后面是羊，剩下的一扇门仍然是羊，不換门能得到汽车，换门得到羊。而在最初选择的门1后面是羊的情况下（概率2/3），其它的两扇门中，一扇门后面是羊，另一扇门后面是汽车，蒙蒂总是打开是羊的门，剩下的一扇门则是汽车，因此，换门得到汽车，不换门得到羊。这就是说：在蒙蒂打开了一扇门展示是羊后，换门得到汽车的概率是2/3，不换门得到汽车的概率1/3。这是因为你在第一次选择时更有可能选到一扇后面是山羊的门，然后蒙蒂总是打开其它一扇后面是山羊的门，换门改变选择会使赢得汽车的概率翻倍。

另一种看待相同选择的方式是将其绘制成决策树，如下图所示：

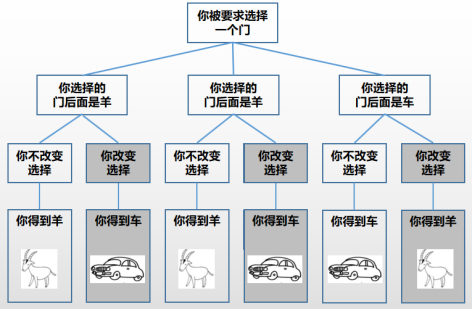
下面利用贝叶斯定理分析蒙蒂霍尔问题。

设H为假设“1号门后面有辆汽车”（我们希望知道的最初选择的这扇门的中奖概率），E是蒙蒂打开了一扇门，揭示了后面有只山羊的门的证据。那么问题可以重新表述为计算P(H∣E)，给定E时H的条件概率。

由于每扇门后要么有一辆汽车，要么有一只山羊，所以“notH”与“1号门后有一只山羊”相同。

在这种情况下，贝叶斯定理指出

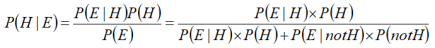
分解这个方程的每个组成部分，我们有以下内容：

P(H)是“门1后面有汽车”的先验概率，这是1/3。

P(notH)是“门1后面是羊”的概率（我们没有选择后面有车的门的概率）。因为门后面要么有汽车，要么没有汽车，所以P(notH)= 1- P(H)= 2/3。

P(E∣H)是在给定H（“门1后面有汽车”）情况下，蒙蒂展示一扇后面有一只山羊的门的概率。由于蒙蒂总是展示一个有山羊的门，所以这等于1。

P(E∣notH)是在给定notH（“门1后面是一只山羊”）情况下，蒙蒂展示山羊的概率。同样，由于蒙蒂总是展示一个有山羊的门，所以这等于1。

综合所有这些信息得出

在门1（最初选择门）后面的有汽车的概率完全不受证据影响。然而，由于汽车只能在门1后面或蒙蒂没有打开的门后面，所以汽车在未打开的门后面的概率是2/3。因此，对于蒙蒂霍尔问题，中奖得到汽车的概率，选择换门是不换门的两倍！

[ 蒙蒂霍尔问题变种的解 ]

前面讨论的蒙蒂霍尔问题得到的结果，在很大程度上取决于这样一个事实：不管你最初选的是哪扇门，蒙蒂总是打开一扇后面有山羊的门。那就是P(E∣H) = P(E∣notH)。

下面考虑蒙蒂霍尔问题的变种——如果蒙蒂真正随机地打开一扇门，现在里面恰好有一只山羊，会发生什么？不管我们选择了哪扇门，第一次选择正确的概率是多少？

当最初选择的门后面是汽车时，蒙蒂向我们打开的门后面有一只山羊的门的概率P(E∣H)仍然是1。这是因为如果你选了有车的那扇门，另外两扇门的后面肯定会是山羊，不管蒙蒂打开哪一扇门都是羊。

但是，当你最初选择的门后面是山羊时，蒙蒂选择打开一扇后面是山羊的门的概率P(E∣notH)变了。这因为在这种情况下，蒙蒂随机地在后面是山羊的门和后面不是山羊的门之间选择。因此，他选择后面是山羊的门的概率是P(E∣notH)=1/2。

这样，我们得到：

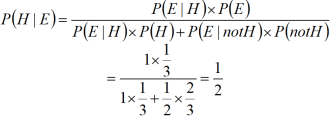
所以，当蒙蒂随机地打开一扇门，而门后恰好有一只山羊时，我们的第一次选择有1/2或50%的可能性是正确的。也就是说，对于蒙蒂霍尔问题的变种，选择换门不会增加中奖可能性。

涉及贝叶斯推断的争议

贝叶斯推断曾经是统计学中颇有争议的方法。对贝叶斯方法的基本反对意见有来自两个方面（参考资料[3]）：一方面，贝叶斯方法被认为是一种自动推断引擎，这引起了有实际经验的人的怀疑；另一方面的反对意见来自相反的方向，针对的是贝叶斯推断的主观性。

比如，1990年，一名男子在英国被判强奸罪，并被判处16年监禁——部分依据是DNA证据。控方的一名专家证人表示，DNA与另一个人相同的可能性只有300万分之一。但该男子对这句话提出上诉。一位专家声称，这样的推理存在缺陷，因为这一证据混淆了两个问题：假设一个人是无辜的，他的DNA与样本中的DNA匹配的可能性有多大？如果DNA与样本相匹配，他们无罪的可能性有多大？虽然只有三百万分之一的机会匹配DNA，但总人口约为6000万。这意味着有20个人会有匹配的DNA，其中一个会被判有罪。如果随机选择一个，那么就会有19/20即95%的机会选择一个无辜的人——这确实看起来很高，被称为“检察官谬误”。DNA证据本身不足以确保定罪，当然，若有其他证据则会降低谬误的可能性。例如，如果知道在受害者被强奸时20个人中没有其他人在那个区域，那么将这个证据应用到贝叶斯公式，会增加被告有罪的可能性。贝叶斯推理是一个概率更新的过程，每一个新的证据都可以确证有罪的可能性。

在非常大的系统中应用贝叶斯推理也会遇到困难，因为构成假设的证据项必须相互独立。这意味着所使用的两项证据不能相互影响。对于存在大量的假设和证据，可能导致相互关联的假设和证据数量的组合学爆炸。当然，通过对数据应用机器学习，可以避免大量的手工编码。

历史上，由于贝叶斯推理建立在“先验概率”概念基础上，曾经被认为“不可靠”，在19世纪末、20世纪初受到过乔治·内曼、罗纳德·费希尔等批评，一度被扼杀。20世纪50年代，得益于丹尼斯·林德和莱昂纳多·萨维奇等人工作的推动，贝叶斯统计得以复兴。

结语

托马斯·贝叶斯是第一个为概率推理建立了数学基础的人。贝叶斯定理在贝叶斯生前并没有发表，1763年（贝叶斯逝世后两年）才在由理查德·普莱斯（Richard Price）整理发表的贝叶斯论文《An Essay towards solving a Problem in the Doctrine of Chances》中公之于众。贝叶斯定理是概率论与数理统计的有力工具，可以说，贝叶斯定理在概率论中的地位相当于勾股定理（毕达哥拉斯定理）在几何学中的地位。

贝叶斯定理是概率建模和数据科学以及机器学习中推理的核心。由于其在更新预测时提供的灵活性，在许多领域得到了广泛的应用。在第二次世界大战期间，艾伦·图灵（Alan Turing）及其同事在破解德国恩尼格玛密码中，成功地使用贝叶斯方法来猜测消息中的字母，并在新数据到达时添加更多线索。在20世纪70年代，美国地中海潜艇舰队指挥官约翰·尼科尔森（John Nicholson）利用贝叶斯计算机分析，来确定苏联核潜艇最可能的航线。1988年，朱迪亚·珀尔（Judea Pearl，图灵奖得主）发明了贝叶斯网络，这是一种基于概率的不确定性推理网络。如今，贝叶斯数学帮助识别图像、筛选垃圾邮件、处理自然语言、评估医疗和国土安全风险、解码DNA，以及彻底改变机器人技术——通过用概率分布来表达所有信息，从有限和不确定的证据中产生可靠的估计。谷歌的无人驾驶汽车通过从车顶传感器获取的新的道路和交通数据更新地图信息，谷歌希望更好地利用这个250年前的定理的方法，降低汽车能源消耗，使车辆能更加安全地行驶在拥挤的道路上。

参考资料：

[1] Dennis Sun. Introduction to Probability. 2020-8-14

(dlsun.github.io)

[2] Christopher Williams, Adam Strandberg, Ansh Bha. Monty Hall Problem.

https://brilliant.org/wiki/monty-hall-problem/

[3]Andrew Gelman. Objections to Bayesian statistics.Bayesian Analysis (2008) 3, Number 3, pp. 445–450