约翰内斯·开普勒（Johannes Kepler）曾经把毕达哥拉斯定理（即勾股定理）和黄金比例（也称黄金分割）称为“几何学的两大宝藏”。前面两篇博客讨论了勾股定理，本篇讨论的比内特公式涉及黄金比例和斐波那契数列。比内特公式远不如黄金比例和斐波那契数列广为人知，但是它连接了黄金比例和斐波那契数列。

斐波那契数列Fn（n=1,2,3,..）：

1，1，2，3，5，8，13，21，34，…

与黄金比例紧密相连——当我们取任意两个连续的(一个接一个)斐波那契数时，它们的比率非常接近黄金比例φ。

两年前，我在科学网博文《神奇的斐波那契数列（2021-2-22）》中，列举过斐波那契数列的一些简洁、美丽的公式，其中，有一些公式，涉及黄金比例φ：

这里所列的最后一个公式，称为比内特（Binet）公式，可用于寻找斐波纳契数列的第n项。之所以这样命名，它是由雅克·菲利普·玛丽·比内特（Jacques Philippe Marie Binet,1786.2.2—1856.5.12），在1843年推导出来的，尽管莱昂哈德·欧拉、丹尼尔·伯努利和德·莫维尔在一个多世纪以前就知道这个结果。比内特致力于矩阵理论的基础研究，他最为人知的成就是发现了矩阵乘法规则。

公式

总所周知，斐波那契数列由

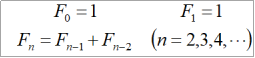     ....（1）

定义。如果按照定义进行计算，为了计算第100个斐波那契数，我们需要先计算它之前的所有99个值。因此，一个自然会提出的问题是:我们能为F(n)找到一个直接计算第n项而不需要计算任何其他(更早的)斐波那契值的公式吗？是的，这个涉及到我们的黄金比例数:

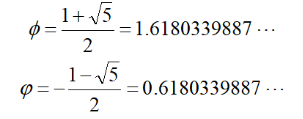
 比内特公式是说：如果F_n是第n 个斐波那契数，那么

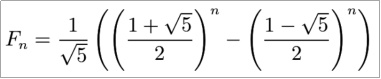   ....（2）

例如，对于n=25,

因此，斐波纳契数列的第25项是75025。

证明

为了推导出斐波那契数的一般公式（2），回顾黄金比例的定义：黄金比例或黄金分割比，是一条线段被切割成两段不同长度的比值，使得整条线段与较长线段的比值等于较长线段与较短线段的比值。这个数字的起源可以追溯到欧几里德，他在《原本》中提到它是“极端和平均比率”。就当今代数而言，假设较短线段的长度为一个单位，较长线段的长度为x个单位，则得出等式(x+1)/x = x/1。这可以重新排列形成二次方程：

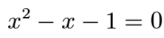
首先注意，这个二次方程的解是：

这个二次方程也可以写成

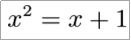
由此，我们可以为所有xⁿ写出表达式：

可以用数学归纳法推出一般公式

     ....（3）

这里，只要假设n=k时，有：

则当n=k+1时，

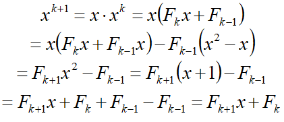
即证明了（3）。

原始二次方的根σ和τ必须满足

所以

和

从第一个方程式中减去第二个方程式得到

这产生了第n个斐波那契数的一般形式

证毕。

结语

比内特公式建立起了黄金比例与斐波那契数的关系。香港科技大学的COURSERA课堂笔记（参考资料[1]）对此有广泛的讨论。

黄金比例被认为是最美丽的，并且在建筑和艺术中被广泛使用。它在自然界的许多地方都可以找到，比如在花瓣中，在蜗牛和鹦鹉螺的螺旋线中，甚至在宇宙中的星系中...。说无处不在，是夸大其词。但是，在简单的几何图形中取距离比值时，黄金比例的确是经常会遇到的数字之一，比如五边形、五角星、十边形和十二面体。

黄金比例φ和圆周率π、欧拉数e都被称为无理数。这些“无理数”不是凭空臆造的，既非“无理”，更非“无用”。研究这些“无理数”大有用处。

参考资料：。

[1] Jeffrey R. Chasnov. Fibonacci Numbers and the Golden Ratio

https://www.math.hkust.edu.hk/~machas/fibonacci.pdf