层状和梯度材料断裂力学的新型边界元方法分析的简介

岳中琦

中国力学学会，2019年4月9日在学会网站，发布了第五届科学技术奖初评通过的四个项目公示http://www.cstam.org.cn/article/201580.html。

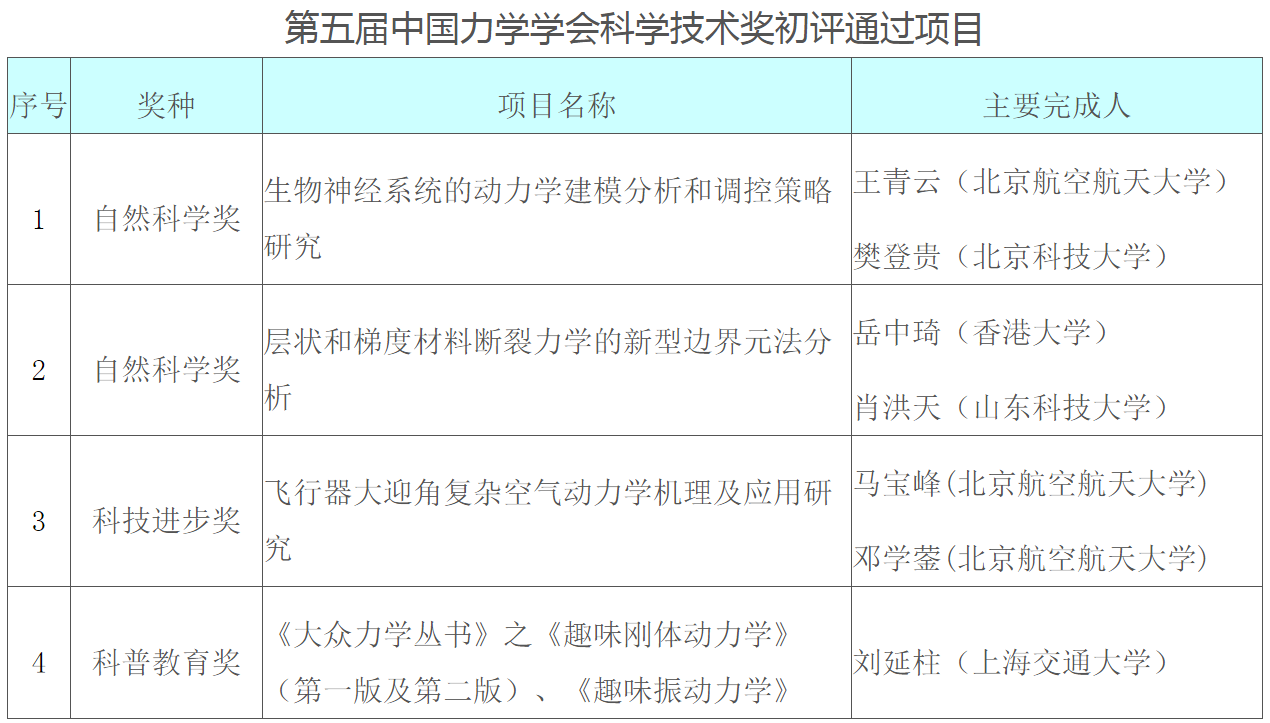
我和山东科技大学肖洪天教授合作研究项目《层状和梯度材料断裂力学的新型边界元方法分析》是其中奖种为自然科学奖的两个项目之一。为此，我们由衷感谢中国力学学会和评审专家们！

我们自2000年以来采用了n层各向同性层状材料的基本解和橫观各向同性双层材料的基本解，发展了新型边界元方法，精确求解了层状和梯度材料的断裂力学问题研究，进一步推动了边界元方法的发展，更加精确地预测了层状和梯度材料的断裂力学特性。

20年来，我们建立了用于分析层状和梯度材料断裂力学边界元方法完整体系。考虑裂纹上下面共面的特性，直接应用传统边界元方法分析裂纹时会遇到数学上的困难。在解决这一问题时，我们发展了两类方法：多区域法和单区域法，成功地解决了这一困难。为了捕获裂纹尖端应力场和位移场的特点，在发展的边界元方法中引入多种奇异单元，提高了计算的精度。采用分层逼近的方法解决了梯度沿梯度材料的厚度方向力学参数任意形式的变化。

我们预测了梯度材料中不同类型裂纹的力学特性。采用发展的边界元方法分析了梯度材料中币型裂纹、椭圆形裂纹、矩形裂纹。提供大量的应力强度因子数据，预测了裂纹的扩展方向和扩展的临界荷载。

我们进一步预测了层状橫观各向同性材料中不同类型裂纹的力学特性。采用发展的边界元方法分析了横观各向同性双层介质中币型裂纹、椭圆形裂纹、矩形裂纹。考虑了橫观各向同性面与裂纹面之间相对位置对裂纹的影响，并提供大量的应力强度因子数据。

边界元法由于只需在边界上离散和基本解的奇异性特性，相比其它数值方法，如有限元法，在解决断裂问题上具有天然的优势。传统的边界元法采用了均匀各向同性介质的Kelvin基本解，限制了这种数值方法在梯度材料的广泛应用。上述的n层各向同性层状材料的基本解，由于n可以为任意大小的正整数，使得边界元方法分析梯度材料成为可能。第二个橫观各向同性双层材料的基本解，也使得边界元方法分析双层橫观各向同性材料成为可能。由于层状材料良好的力学特性，层状材料在各种工程结构中得到了广泛应用。近30年来，新型复合材料功能梯度材料出现和在工业制造领域得到的应用，使得这种新型材料的断裂力学特性成为科学家的研究热点。边界元数值方法是精准分析断裂力学特性的重要工具。相关工作可进一步参见博文《一本断裂力学英文专著的出版发行》http://blog.sciencenet.cn/blog-240687-1122365.html。

2020年9月2日20:50写成于香港大学602办公室