每期文章评述的首发平台是微信公众号：近场动力学PD讨论班，也可以搜索微信号：peridynamics，或扫描文末的二维码加入。

2019年9月下期近场动力学领域有四篇新文章上线。其中除了将近场动力学理论用于模拟开裂、冲击碎裂等较为常见的应用工况，本期的第一篇文献还将近场动力学拓展到薄膜的大变形、起皱和破裂分析。由于近场动力学基于两点间的位移差来描述物体的变形，并采用两点键的断裂来描述损伤和破坏过程，因此避免了经典线弹性力学的小变形假设和连续性假设，从而为统一模拟物体从小变形到大变形，乃至破裂的整个连续/非连续变形过程创造了可能性。下面我们依次简要介绍：

文一：

https://doi.org/10.1007/s10409-019-00894-7

基于近场动力学计算框架下的双模结构和薄膜的大变形及起皱分析

本文基于隐式键型PD计算框架，研究了双模结构及薄膜的准静态大变形、起皱和断裂行为。首先，作者分别推导了所涉及的非线性问题的隐式PD方程的常数和切线刚度矩阵。前者在几何近似的基础上通过对键应变的线性化而得到，后者利用一阶Taylor展开通过将对力的线性化而得到。然后，建立了PD双模材料模型，该模型中材料在每一点上的拉伸或压缩行为可以用邻近键的拉伸或压缩状态来描述。此外，通过将压缩微模量置零对双模材料模型进行推广，用以处理薄膜的起皱和断裂问题。然后，利用增量迭代算法得到了非线性问题的收敛解。最后，给出了几个有代表性的数值算例，结果表明了本文所提出的方法对双模结构和薄膜大变形、起皱及断裂分析的精确性和有效性。

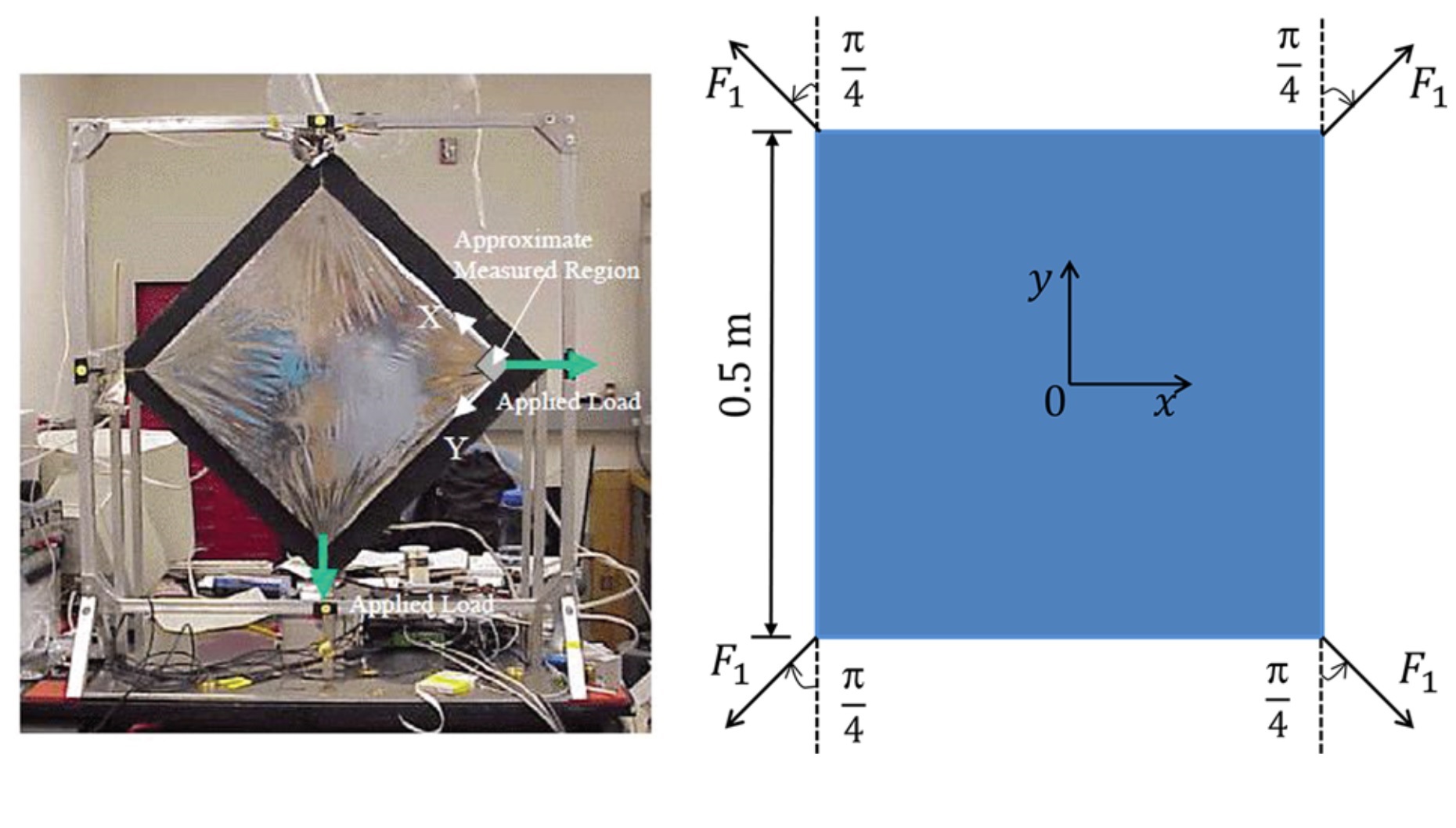
图：方形起皱薄膜：（a）实验模型;（b）数值模型。

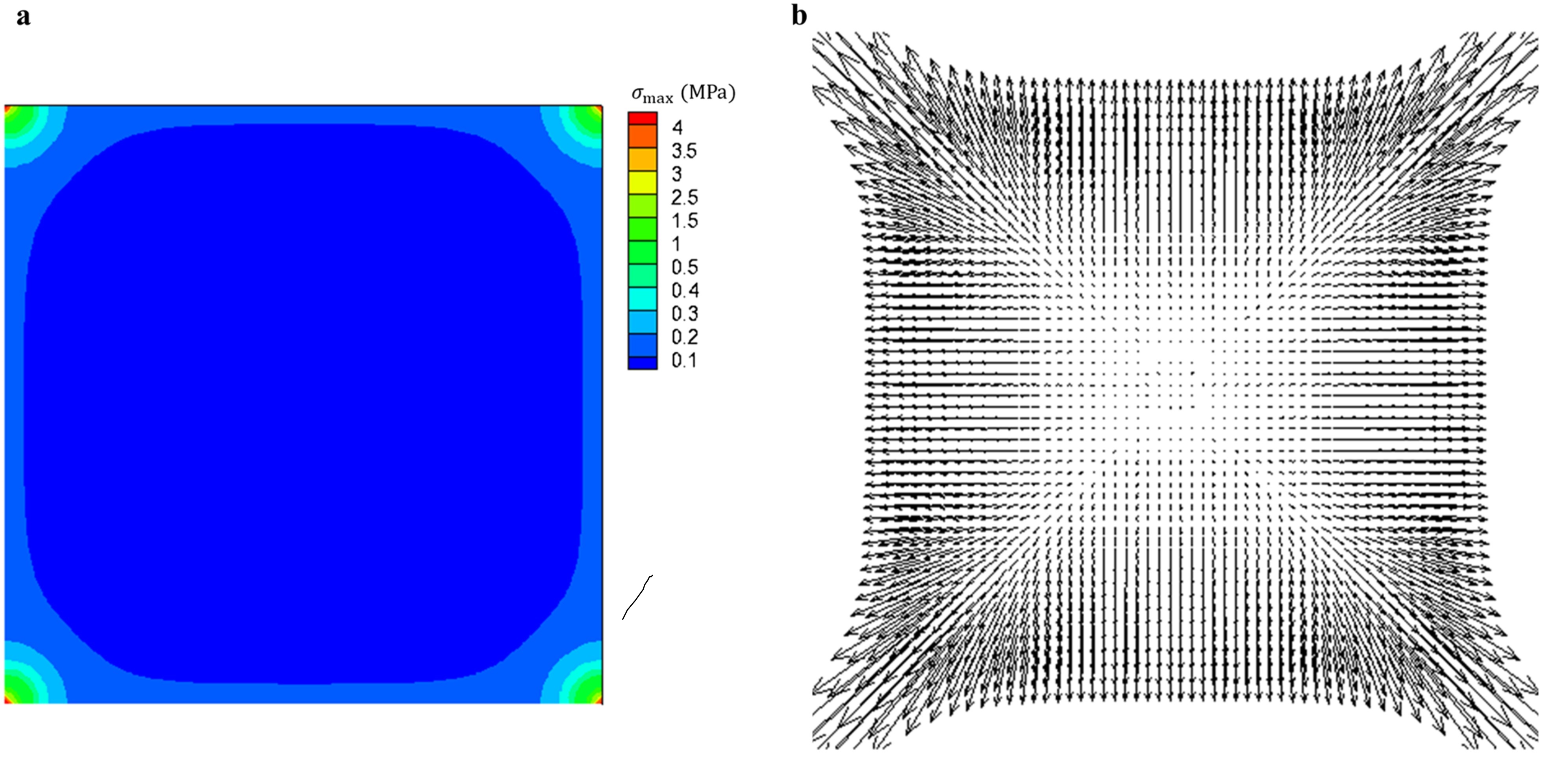
图：应力模式，（a）最大主应力、（b）用文中所提出方法求得的最大主应力大小和方向。

文二：

https://doi.org/10.1002/nme.6234

稳定化非常规态型近场动力学模型的隐格式算法

在本文中，作者们提出了一种稳定化的非常规态型近场动力学模型，它可以克服原先模型由于零能模式而造成的数值不稳定性问题。针对此模型，作者们还给出了相应的隐格式离散公式。为了在粗颗粒离散条件下模拟渐进损伤过程，本文发展了一种基于影响函数的双线性损伤模型。作者们给出了相应的隐格式算法，其中基于切刚度方法的迭代过程被用于求解非线性问题。对于拟静态问题，本求解方法不需要引入阻尼项，并且可以应用相对大的载荷步长。五个数值算例被分析用于量化模拟拟静态的裂纹扩展问题，以展示本文所提出方法的有效性。

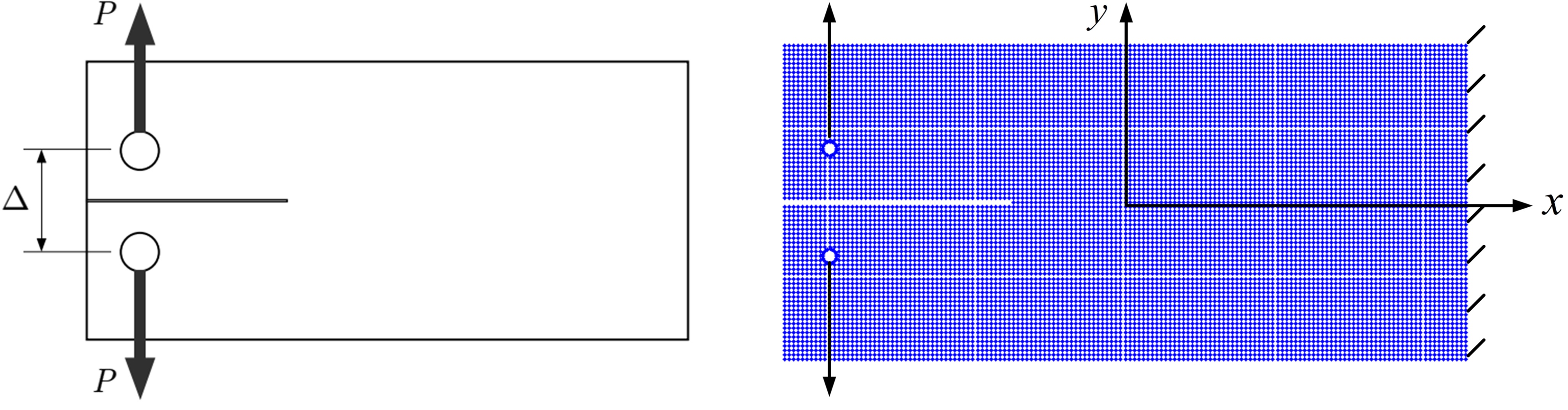
图：右端固定的双悬臂梁，左图：几何模型；右图：近场动力学离散模型。

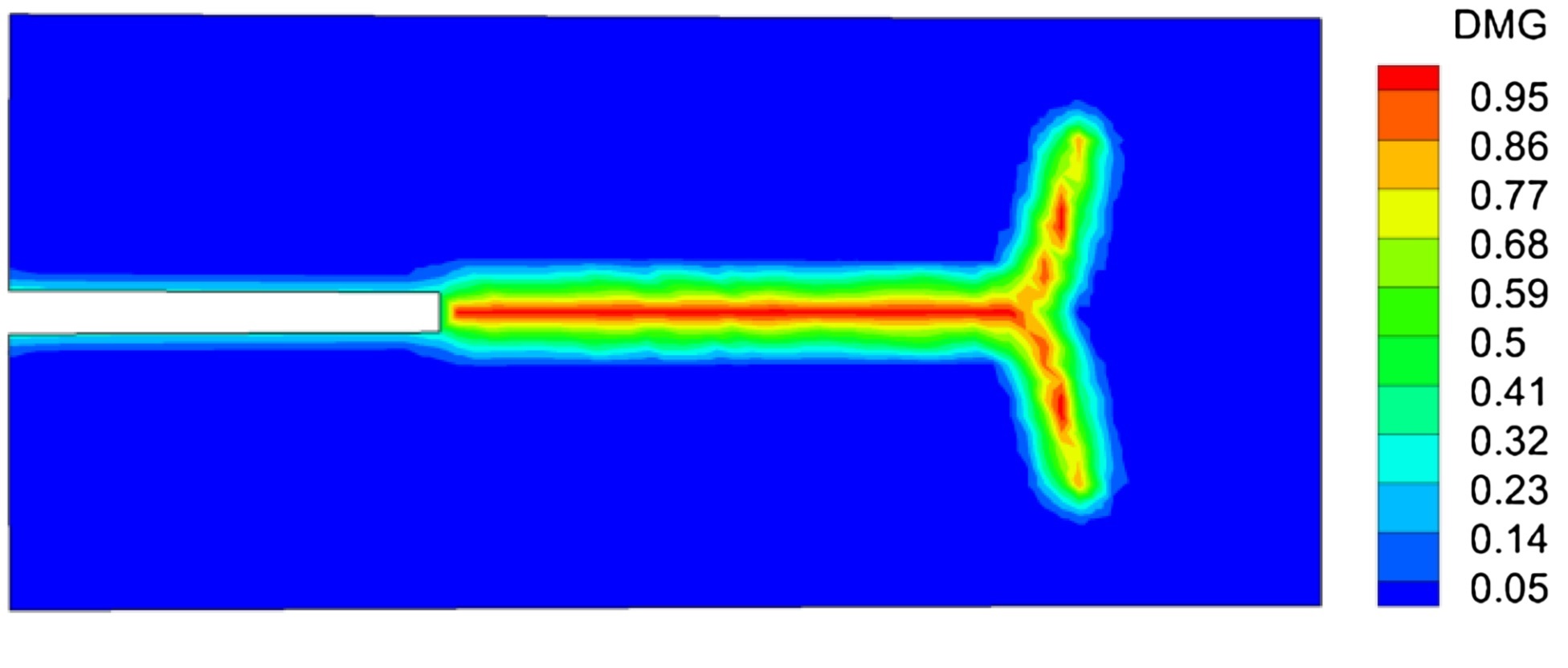
图：右端固定双悬臂梁试件的破坏模式。

文三：

https://www.frontiersin.org/articles/10.3389/fmats.2019.00239/abstract

弹击玻璃致裂:利用近场动力学模拟所得到的新见解。

大多数玻璃在使用寿命中常会受到物体（本文统一称之为弹体）的冲击荷载，这可能会导致玻璃结构的破坏。冲击破坏的实验研究由于冲击时间短而极具挑战性。另一方面，基于连续体的计算研究又由于裂纹扩展引起位移场的不连续而变得很复杂。本文使用近场动力学模拟方法，研究了结构特性和几何形状对受到冲击荷载的玻璃板整体破坏的影响。特别地，作者分析了弹体的速度、弹体材料、弹性模量、断裂能量和板的半径对板破坏的影响。作者观察到玻璃板的破坏和玻璃板断裂能量之间存在幂指数关系。通过对裂纹演化的自回归分析，证明裂纹的自仿射生长确实导致了这种幂指数关系。本研究说明了近场动力学模拟如何为研究玻璃在弹体冲击下的断裂力学提供新的见解。这种改进的求解方式可以为设计和开发出具有更好的抗弹体冲击能力的玻璃，比如应用到挡风玻璃、智能手机屏幕等，提供保障。

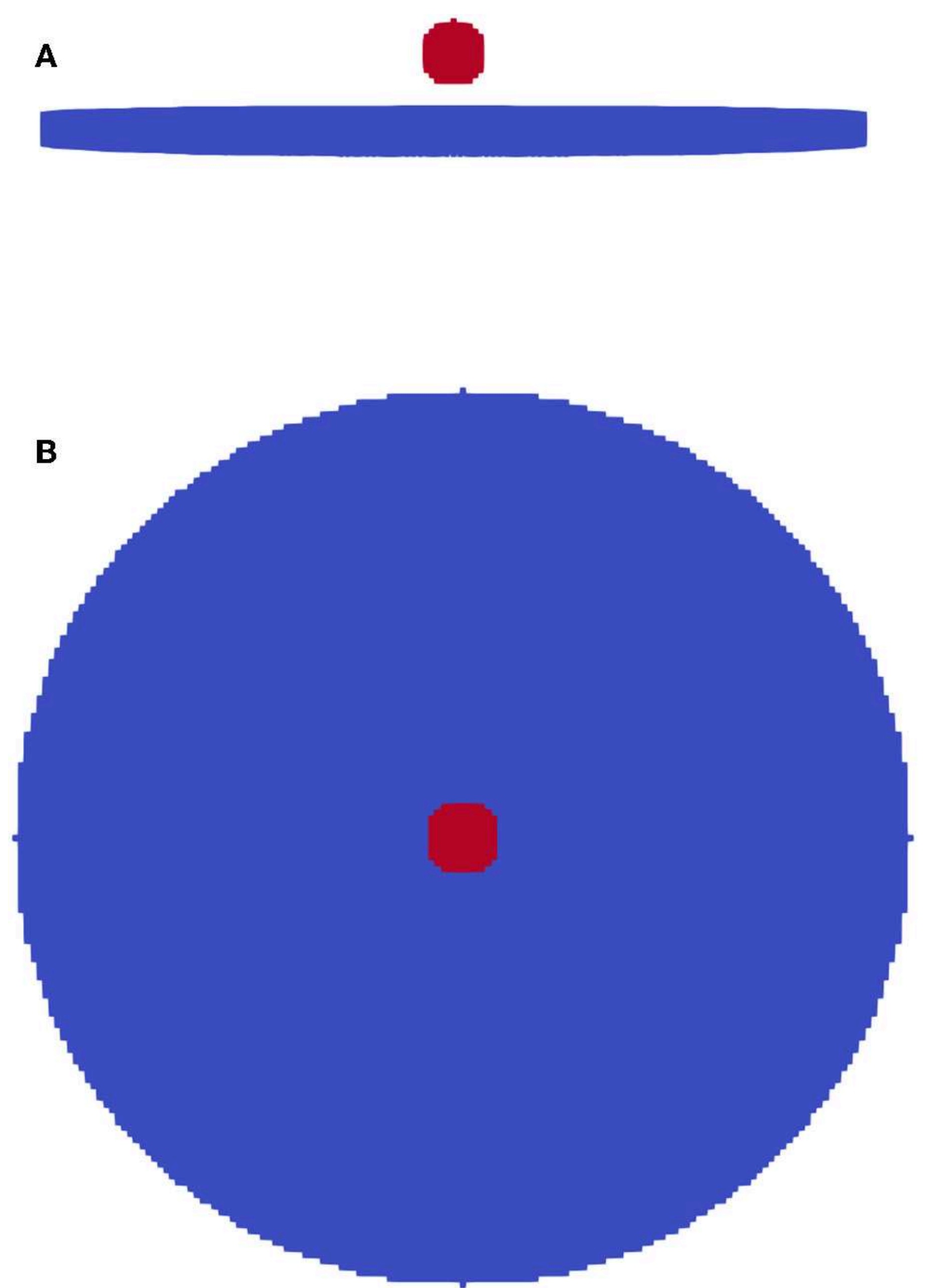
图：子弹冲击板的仿真设置：(a)前视图和(b)俯视图，玻璃板和子弹分别是蓝色和红色的。

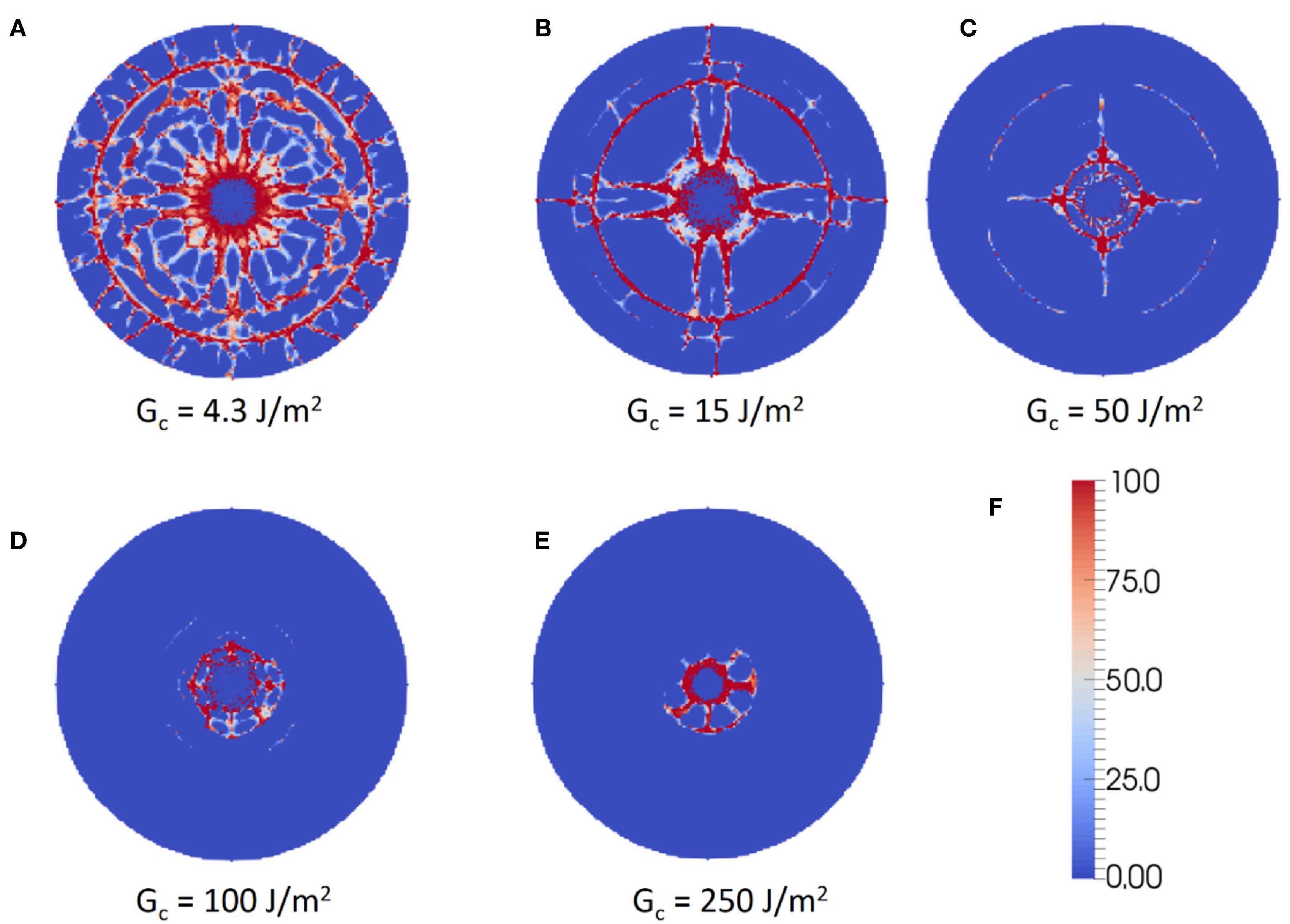
图：（A）模拟的冲击回弹系数与实验结果相比较；（B）钢球以200m/s的速度冲击钠钙玻璃；（C）冲击实验的近场动力学模拟结果，红色代表损伤颗粒。

文四：

https://doi.org/10.1177/1081286519873694

利用近场动力学研究正交异性Mindlin板的弯曲力学性能

复合材料由于优越的强度和刚度，在航空航天、汽车、风能和太阳能系统等领域的应用越来越广泛。复合材料由于其结构复杂，在实际工程应用中，其结构分析还存在许多未解决的问题。近场动力学是分析复合材料结构的一个强大的理论，然而它的计算量非常大。工程中通常将结构进行理想化，并以合理且简单的模型来表示结构，从而降低求解的计算量。例如将一个板理想化为一个平面，可以减少很多近场动力学的求解。本文提出了一个考虑横向剪切变形的正交各向异性板的近场动力学模型。近场动力学键的参数可以通过联立局部的近场动力学运动方程与经典介质连续力学的运动方程来求得。为了进行裂纹扩展模拟，在本研究中应用了失效理论。利用该公式编写了求解正交各向异性板弯曲问题的MATLAB程序。得到了带缺口的板的弹性变形和失效预测的近场动力学解，并用有限元进行了分析验证。

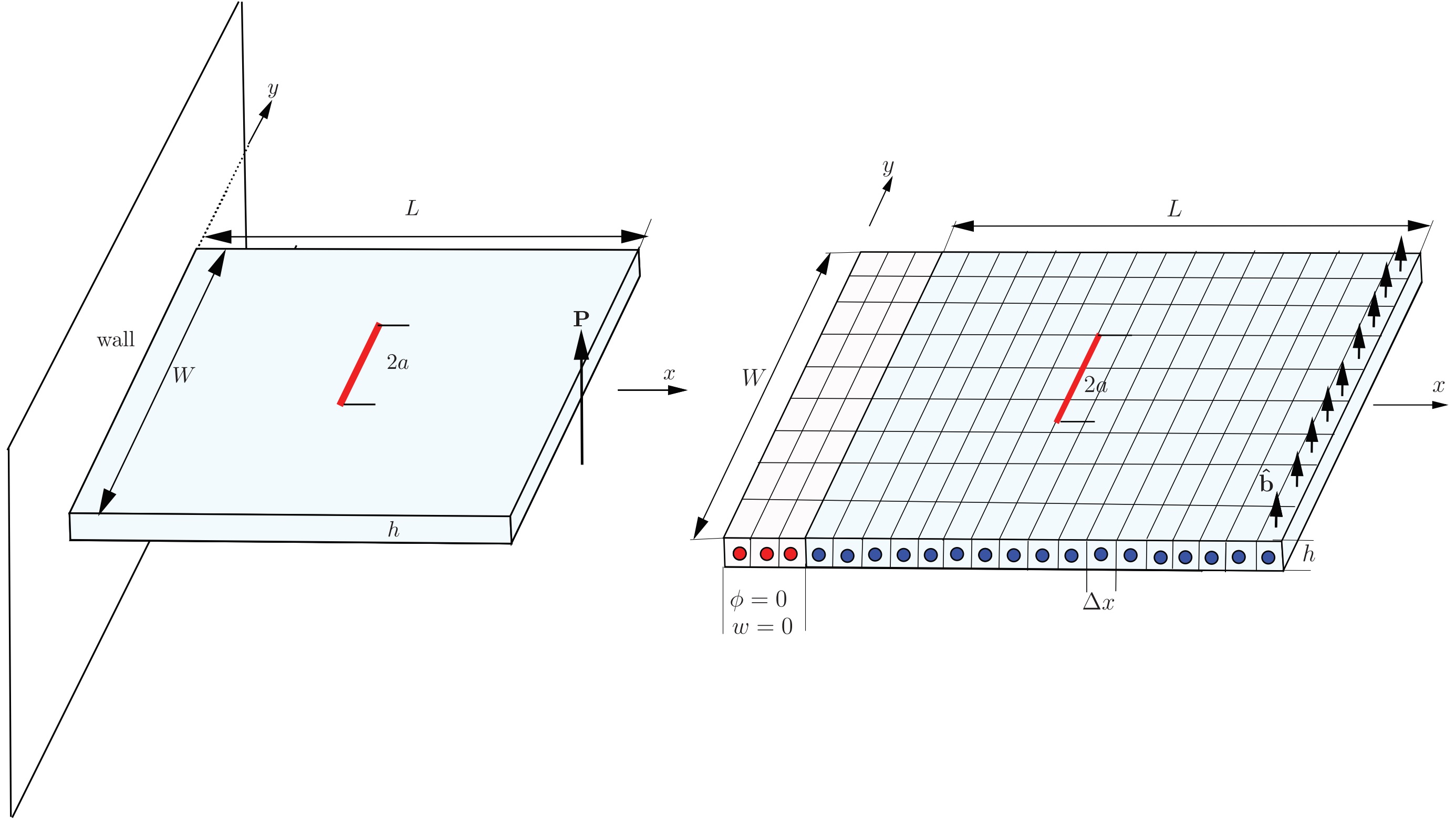
图：横向力作用下预置裂纹的Mindin板。

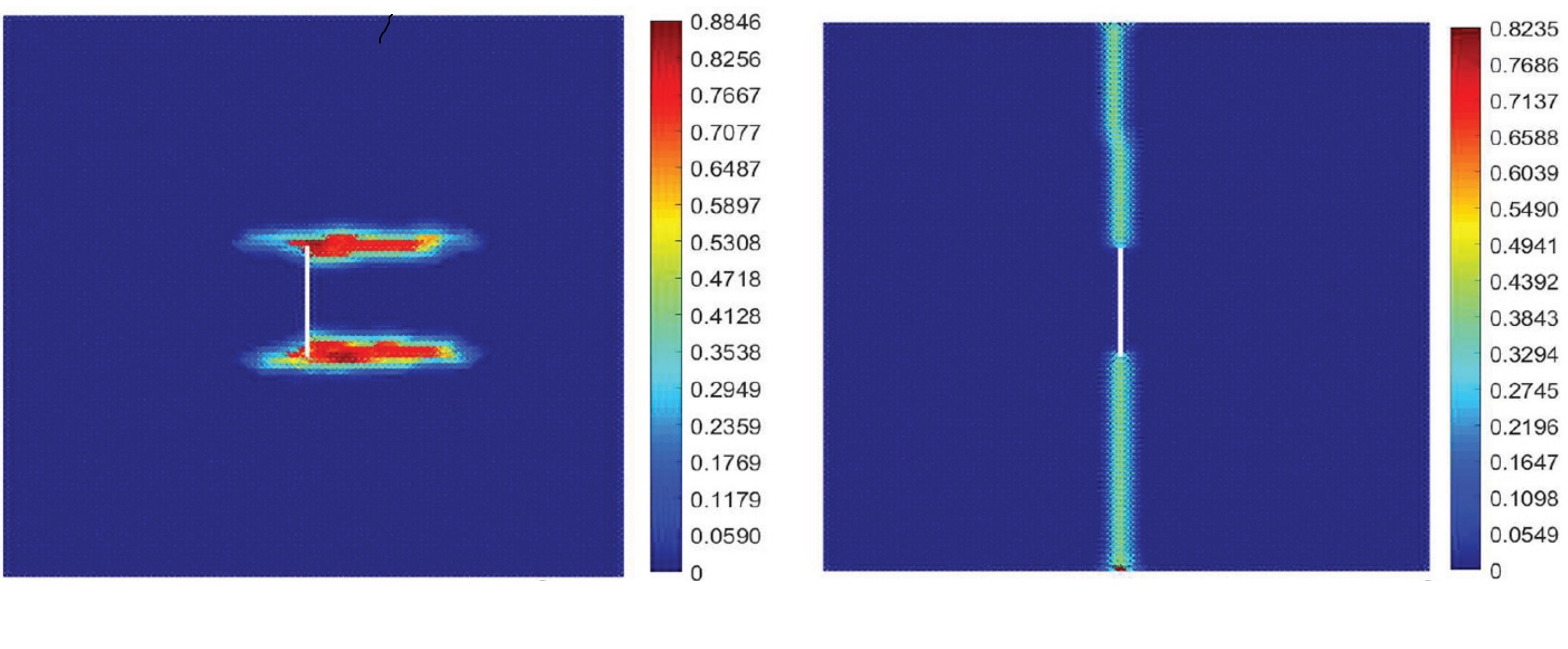
图：方向为0°（左图）和90°（右图）的板在横向力作用下的损伤图。

—————————————————————————————————————————————

近场动力学(PD)理论是国际上刚兴起的基于非局部作用思想建立的一整套力学理论体系，用空间积分方程代替偏微分方程用以描述物质的受力情况，从而避免了传统连续力学中的微分计算在遇到不连续问题时的奇异性，所以特别适用于模拟材料自发地断裂过程。然而，因为近场动力学的数学理论内容丰富且与传统理论差别较大，目前的相关文献又以英文表述为主，所以很多朋友在一开始学习时会遇到一些困难。因此，我于2016年9月建立了此微信公众号（近场动力学讨论班），希望通过自己的学习加上文献翻译和整理，降低新手学习近场动力学理论的入门门槛，分享国际上近场动力学的研究进展，从而聚集对近场动力学理论感兴趣的华人朋友，为推动近场动力学理论的发展做一点儿贡献！

每期文章评述的首发平台是微信公众号：近场动力学PD讨论班
也可以搜索微信号：peridynamics

或扫如下二维码加入公众号：