博文
公设 - 译自《希腊化时代的科学与文化》(3)
||
一,译文
《几何原本》中最令人惊讶的是欧几里德对公设的选择。当然,在这方面亚里士多德是他的老师,亚里士多德对数学原理给予了很大的关注,指出公设的不可避免性和将公设降到最小程度的必要性,然而公设的选择却是欧几里德所做的。
尤其是“第五公设”的选择,也许是他最伟大的成就,它比任何其他成就都更能使“欧几里得”这个名字不朽。让我们逐字逐句地引用它:
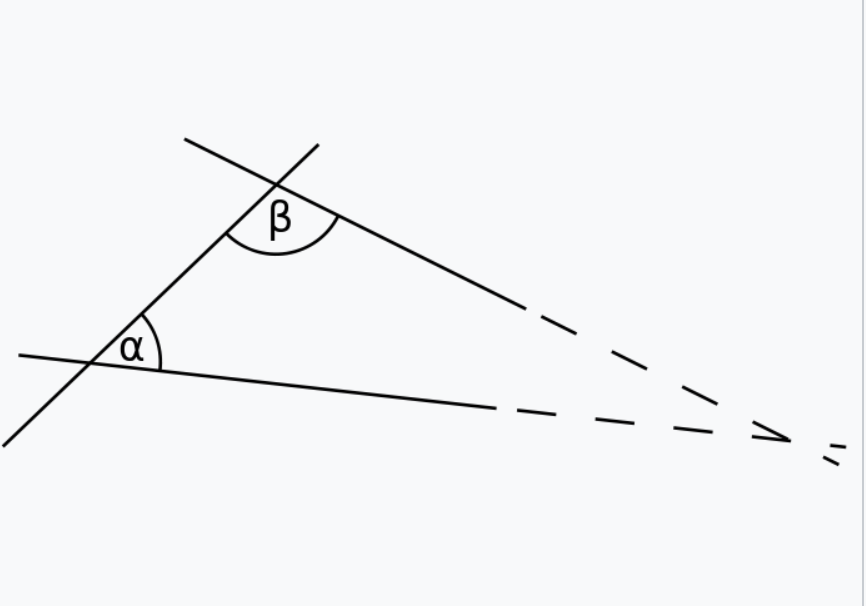
- 如果一条线段与两条直线相交,在某一侧的内角和小于两直角和,那么这两条直线在不断延伸后,会在内角和小于两直角和的一侧相交。
一个普通智力的人会说,这个命题是显而易见的,不需要证明;一个好点的数学家会意识到需要证明,并试图给出证明;只有非凡的天才才能意识到需要证明,却办不到的。那么,从欧几里德的角度来看,没有任何出路,只能接受它作为一个公设,继续前进。
欧几里得这一重大决定表现出其天才,最佳的评价方式是研究其结果。第一个结果,是他的《几何原本》令人钦佩的简洁。第二个结果是数学家们无休止地试图纠正他;首先是希腊人,如托勒密(II-1)和普罗克洛斯(V-2),犹太人列维-本-格森(XIV-1),最后是圣雷莫的Girolamo Saccheri(1667-1733)在他的Euclides ab omni naecovindicatus(1733),瑞士人Johann Heinrich Lambert(1728-77),以及法国人Adrien Marie Legendre(1752-1833)。这个名单还可以延长,但这些名字已经足够了,因为它们代表许多国家和时代杰出的数学家,一直到上个世纪中期。第三个结果是通过列出公设的替代方案来说明的,并成功地做到了这一点,但代价是引入了另一个(明确的或隐含的)与之等同的方案。比如说:
如果一条直线与两条平行线中的一条相交,它也会与另一条相交。(Proclos)
给定任何图形,都存在一个与之相似的任何大小的图形(John Wallis)
通过一个给定的点,只能画出一条与给定的直线平行的线 (John Playfair)
存在一个三角形,其中三个角的总和等于两个直角。(Legendre)
给定非直线的任何三点,存在一个经过它们的圆。(Legendre)
如果我能证明一个直角三角形是可能的,它的内容大于任何给定的面积,我就能完全严格地证明整个几何学。(高斯, 1799)
所有这些人都证明,如果我们接受另一个提供同样功能的公设,那么第五公设就没有必要。接受任何一种选择(上面引用的那些和许多其他的)都会增加几何教学的难度,然而,使用其中的一些会显得非常矫揉造作,会使年轻的学生望而却步。很明显,简单的论述比困难的论述要好;设置可避免的障碍将证明教师的聪明才智,但也证明他缺乏常识。由于欧几里德的天才,他看到了这个公设的必然性,并凭直觉选择了它的最简单形式。
也有许多数学家是如此盲目,以至于他们拒绝了第五条公设,却没有意识到另一条公设正在取代它。他们把一个公设踢出门外,另一个公设则从窗口进来,而他们却没有意识到这一点!
二,原文
Postulates
The most amazing part of that is Euclid’s choice of postulates. Aristote was, of course, Euclid’s teacher in such matters ; he has devoted much attention to mathematical principles, has shown the unavoidability of postulates and the need of reading them to a minimum ; yet the choice of postulates was Euclid’s.
In particular, the choice of postulate 5 is, perhaps, his greatest achievement, the one that has done more than any other to immortalize the word « Euclidean ». Let us quote it verbatim :
- If a straight line falling on to straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.
A person of average intelligence would say that the proposition is evident and needs no proof ; a better mathematician would realize the need of a proof and attempt to give it; it required extraordinary genius to realize that a proof was needed yet impossible. There was no way out, then, from Euclid’s point of view, but to accept it as a postulate and go ahead.
The best way to measure Euclid’s genius as evidenced by this momentous decision is to examine the consequences go it. The first consequence, as far as Euclid was immediately concerned, was the admirable concatenaion of his Elements. The second was the endless attempts that mathematicians made to correct him ; the first to make them were Greeks, like Ptolemy (II-1) and Proclos (V-2), the Jew, Levi ben Gerson (XIV-1), and, finally, Girolamo Saccheri (1667-1733) of San Remo in his Euclides ab omni naecovindicatus (1733), the Swiss, Johann Heinrich Lambert (1728-77), and the Frenchmann, AdrienMarie Legendre (1752-1833). The list could be lengthened considerably, but these names suffice, because they are the names of illustrious mathematicians, representing many countries and many ages, down to the middle of the last century. The third consequence is illustrated by the list of alternatives to the postulates and succeed in doing so, but at the cost of introducing another one (explicit or implicit) equivalent to it. For example,
If a straight line interests one of two parallels, it will intersect the other also. (Proclos)
Given any figure, there exists a figure similar to it of any size (John Wallis)
Through a given point only one parallel can be drawn to a given straight line (John Playfair)
There exists a triangle in which the sum of the three angles is equal to two right angles. (Legendre)
Given any three points not straight line, there exists a circle passing through them. (Legendre)
If I could prove that a rectilinear triangle is possible the content of which is greater than any given area, I would be in a pisition to prove perfectly rigorously the whole of geometry. (Gauss, 1799)
All these men proved that the fifth postulate is not necessary if one accepts another postulate rendering the same service. The acceptance of any of those alternatives (those quoted above and many others) would increase the difficulty of geometry teaching, however, the use of some of them would seem very artificiel and would discourage young students. It is clear that a simple exposition is preferable to one which is ore difficult; the setting up of avoidable hurdles would prove the teacher’s cleverness but also his lack of common sense. Thanks to his genius, Euclid saw the necessarily of this postulate and selected intuitively the simplest form of it.
There were also many mathematicians who were so blind that they rejected the fifth postulate without realising that another was taking its place. They kicked one postulate out of the door and another came in through the window without their being aware of it !
参考文献:
【1】乔治·萨顿(George Sarton)与《希腊化时代的科学与文化》 ,http://blog.sciencenet.cn/blog-2322490-1292301.html
【2】张卜天译本,兰纪正、朱恩宽译本。
https://blog.sciencenet.cn/blog-2322490-1309778.html
上一篇:《几何原本》 - 译自《希腊化时代的科学与文化》(2)
下一篇:非欧几里得几何 - 译自《希腊化时代的科学与文化》(4)