(本文首发于个人知乎：镜子博物馆：不简单的镜子组合 - 知乎)

镜面操作看似简单常见，但是镜子的排列组合可以形成很多有意思的对称性和群，下列举6种常见的组合。

1. 一个镜子：镜面对称性

图1 照镜子的时候，左右颠倒而上下不颠倒

为什么照镜子的时候，左右颠倒而上下不颠倒呢？在物理学中有两种矢量，一种是极矢量（中心反演下反号，例如位置、速度、加速度、动量），另一种为轴矢量（中心反演下不反号，例如：角速度、角动量、磁场、电子的自旋）。因为上下是极矢量，而左右可以用轴矢量描述，因此用轴矢量和极矢量和解释照镜子过程中的这一疑惑。

2. 两个垂直镜子：看到四个自己、左右不颠倒

两个垂直镜子构成的群为C2v，具有四个对称性操作，两个镜面可以衍生出二重旋转对称性(对角线方向的两个对称体之间由C2联系)。

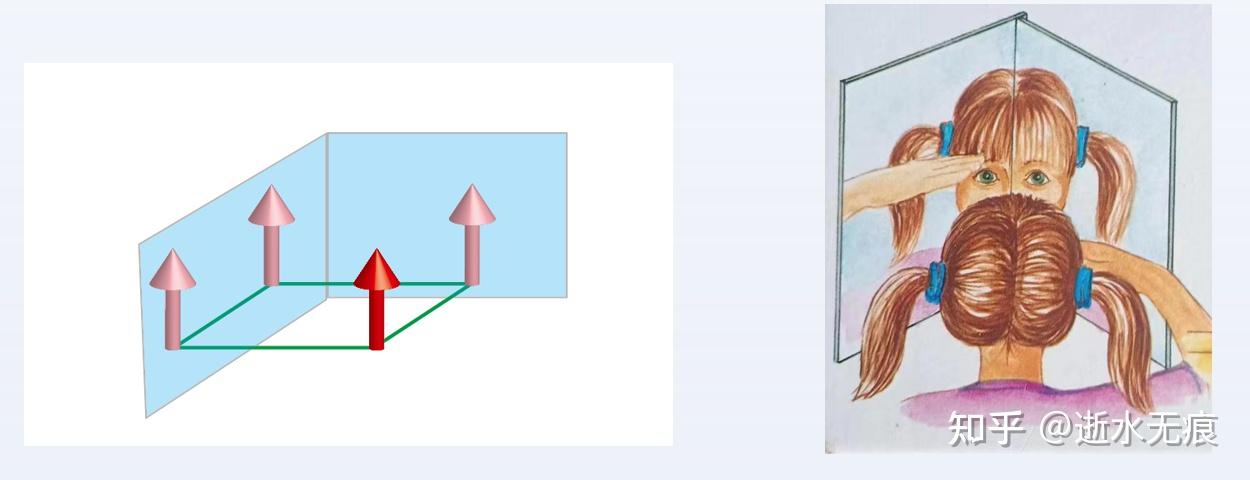
图2 两个相互垂直镜子成像原理（左）。沿着对角线方向看自己的像，像和自己具有相同的左右定义（右）。

3. 三个相互垂直的镜子：借光发亮的角反射器

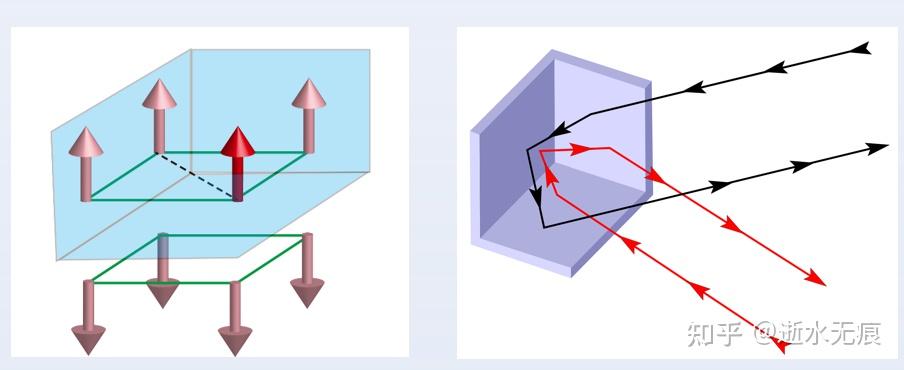图3 三个相互垂直镜子成像特点（左） 角反射器的三次镜面反射的光路（右）

• 构成的群为mmm，三个镜面操作的组合得到中心反演操作。

• 成像特征：可同时呈现8个完全对称体，其中包括一个中心反演形成的倒立像；

• 光路特性：遵循入射光与反射光路径完全重合的逆向反射原理（三次镜面操作的结果一定是中心反演操作，因此光线一定反向）；

• 应用优势：光线怎么来的就怎么回去，能轻松实现借光发亮，例如自行车尾灯和雷达角反射器。

图4 自行车尾灯和角反射器

4. 万花筒：三镜汇聚得三次旋转对称性

万花筒构造：3片长条形平面镜，以60°拼接成空心等边三棱柱，一端装有彩色碎片（如玻璃珠、塑料片等），可自由转动。

原理：三个镜面操作形成六边形无限重复的蜂窝状图案，将简单的物理反射转化为视觉艺术。构成的群为C3v。

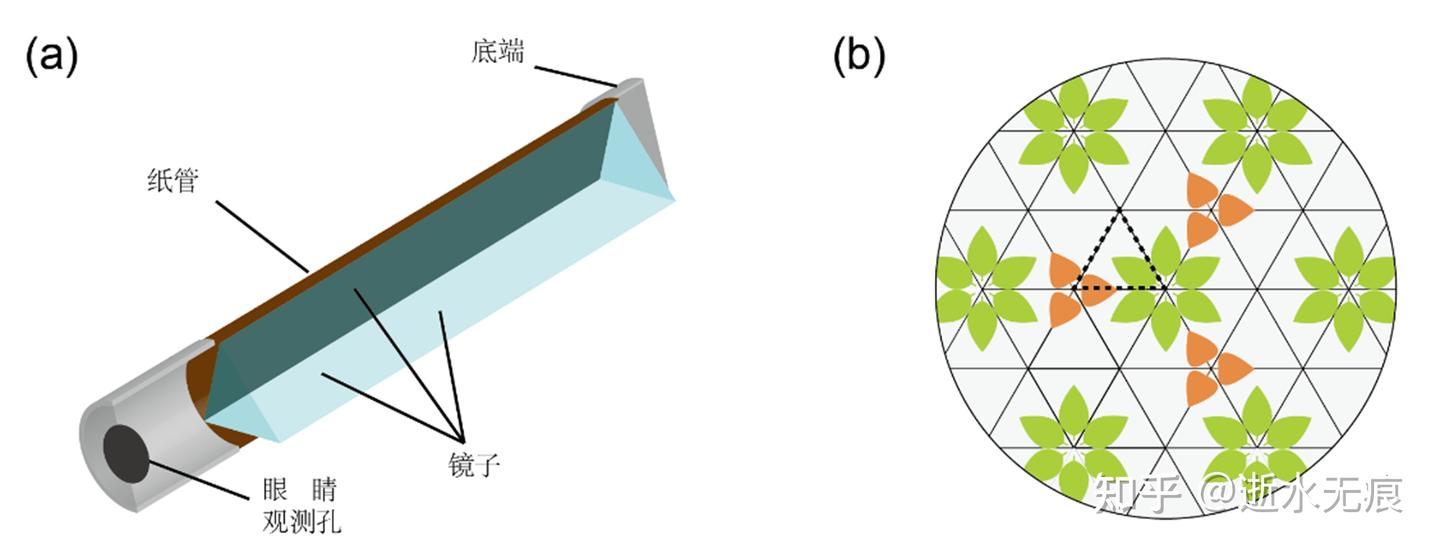
图5 万花筒的构造和成像特征

5. 两个相互平行的镜子：无限反射 深渊镜

两个平行镜面操作无限反射，构成了一维平移群。

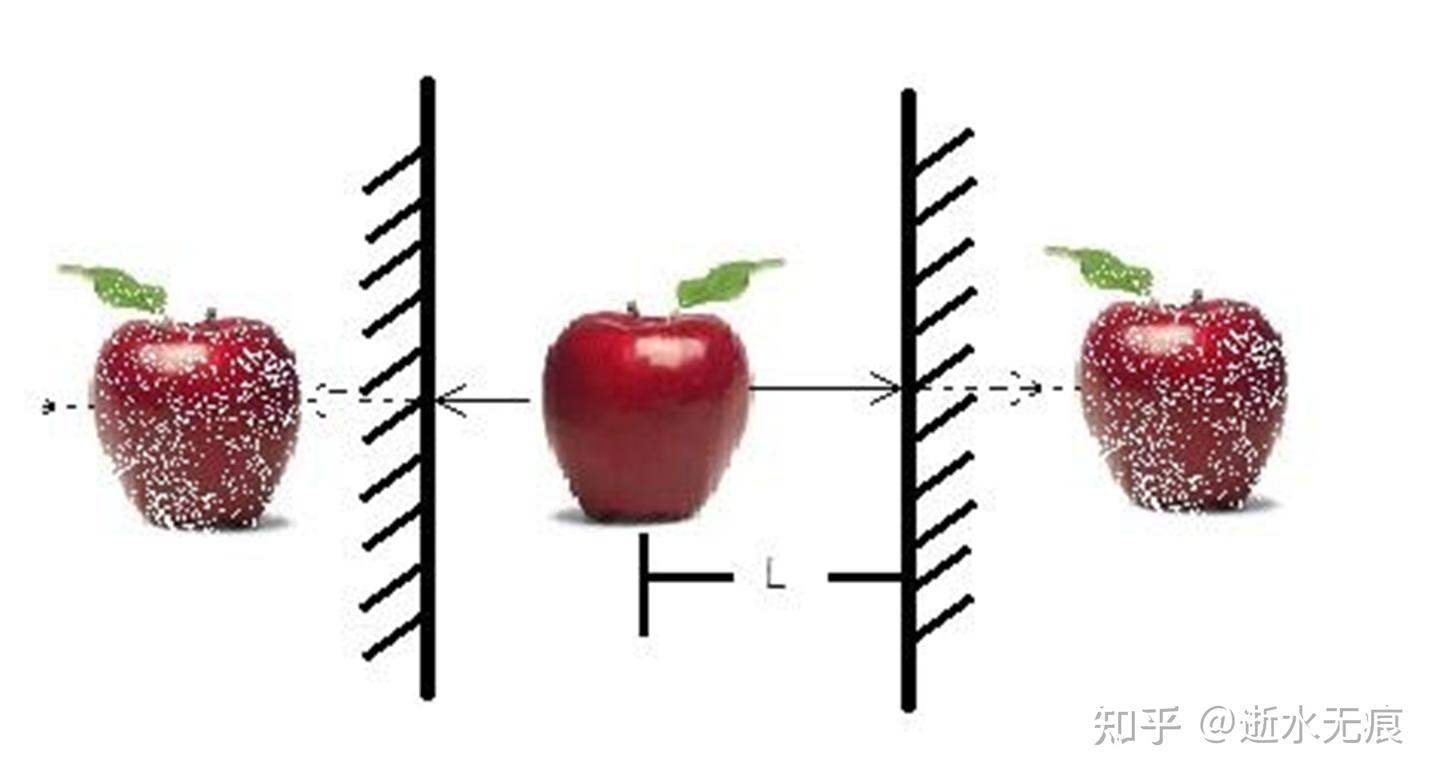
图 6 两个相互平行镜子的成像

图7 深渊镜

6. 两个相互平行的镜子：两次反射 潜望镜

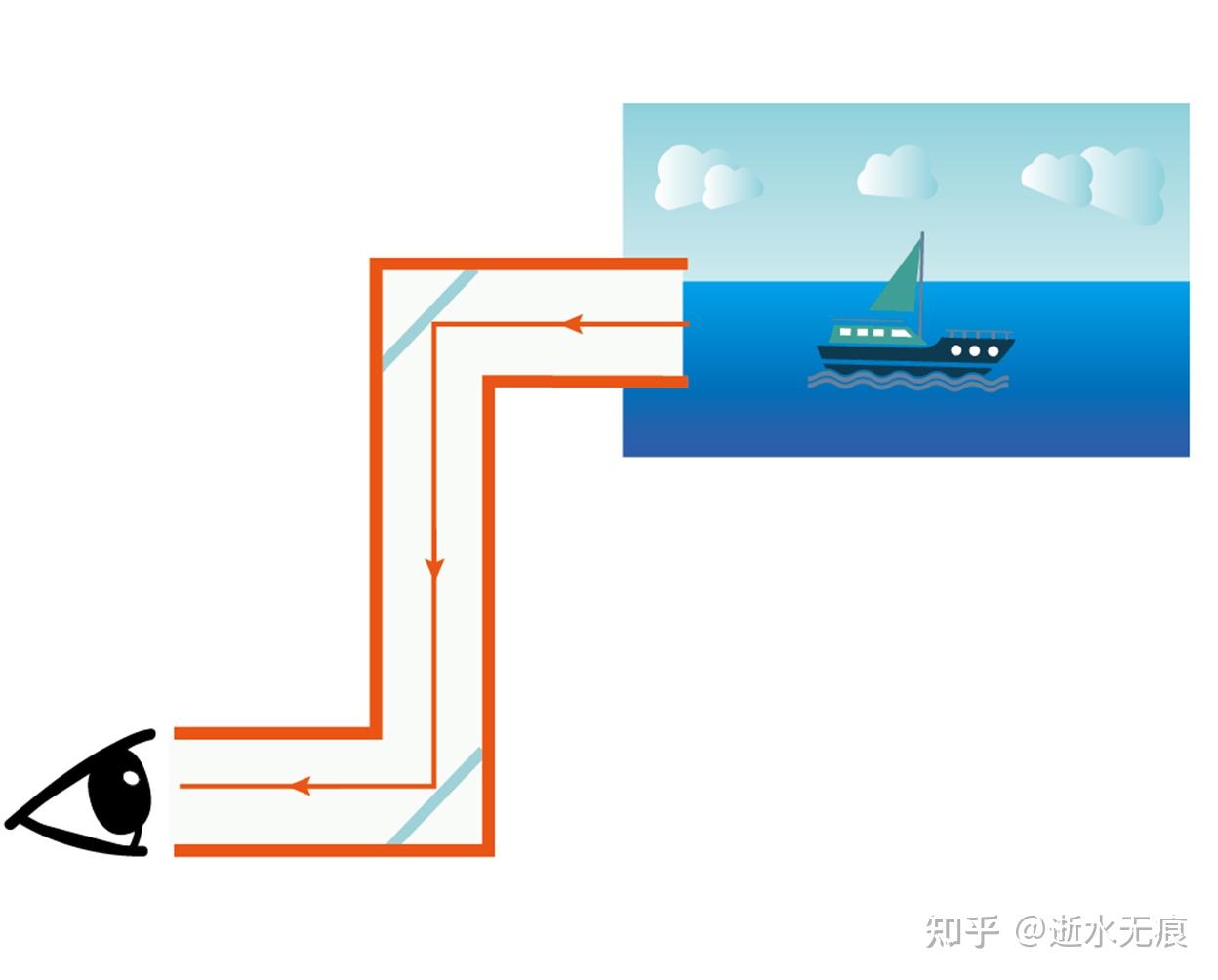
图8 两个相互平行的镜子构成潜望镜

潜望镜是一种利用光的反射原理，使观察者能在隐蔽位置（如潜艇、战壕）看到外界景象的光学仪器。它的核心结构基于平面镜或棱镜的组合，通过改变光路实现视线延伸。

小结：当两个镜子垂直于纸面放置，并且它们之间夹角是如下角度时，能看到的像的个数以及对应的群如下所示。

图 9  镜子之间夹角以及形成的群

转载本文请联系原作者获取授权，同时请注明本文来自肖瑞春科学网博客。
链接地址：https://blog.sciencenet.cn/blog-1502061-1509444.html

上一篇：“群论的应用”系列博客链接
下一篇：把声子模式anime.ascii文件生成可以用VESTA打开的程序