博文
光滑圆锥曲线内的细杆稳定平衡
|||
文[1] 提出均匀细杆置于光滑圆锥曲线内壁的稳定平衡问题,并在直角坐标系中分析了双曲线情形。细杆一端直立于曲线顶点是不稳定平衡;而两端支承于壁面在重心高度达到极小值时稳定平衡;据此可利用中学数学知识给出统一说明,并确定细杆稳定平衡时重心轨迹[2]。
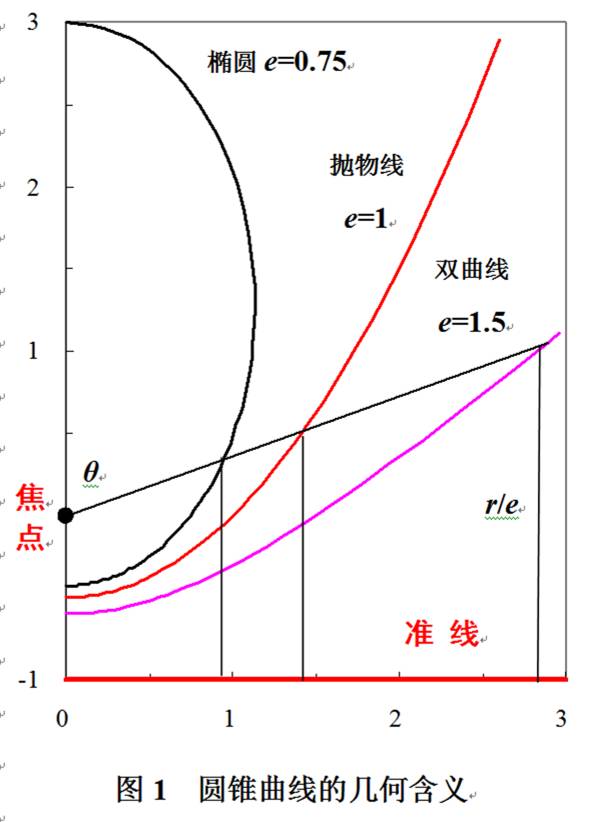
圆锥曲线是距焦点和准线的距离比值,即离心率e为常数的轨迹(图1),有椭圆(0 < e <1)、抛物线( e = 1)、双曲线(1< e )。e= 0为圆,准线在无限远;除此之外,记
焦点与准线间距离为p,极点为焦点P,角度θ从竖轴起算、顺时针为正,则极距r =ep/(1–e cosθ) 随θ增加至π而单调减小。θ=π/2,r =ep;θ=π 即顶点处r =ep/(1+e);而顶点距准线 p/(1+e)。
与竖直线夹角θ、过焦点P的弦长L和中点M的极距分别为
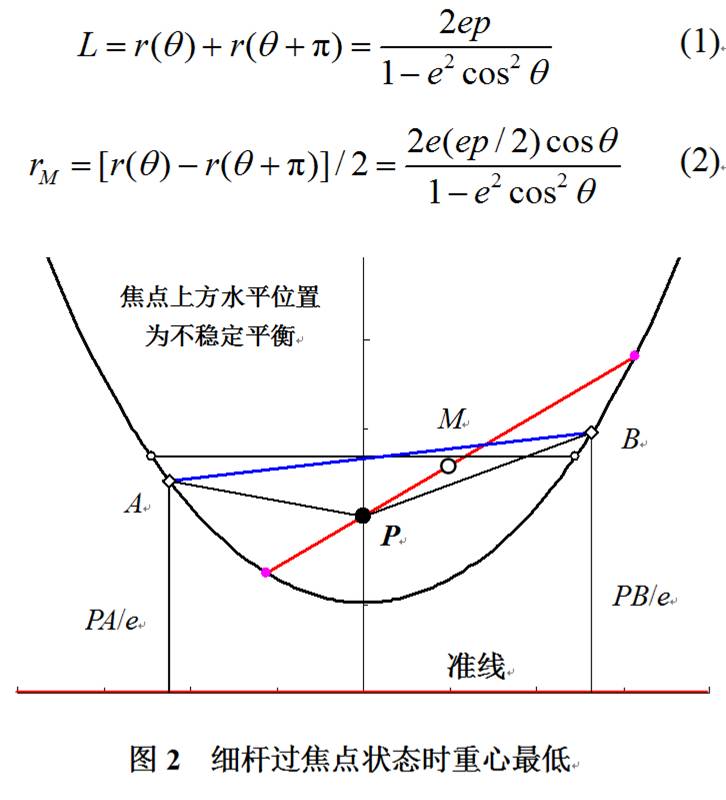
细杆只要长度L大于2ep就可通过焦点。细杆中点M距准线的距离为 (PA+PB)/ 2e;因三角形两边之和PA+PB大于第三边L,知道细杆通过焦点时重心最低,也就是稳定的平衡位置(图2中红色线段),而水平放置是不稳定平衡。
相应的重心轨迹即式(2)为离心率e相同的圆锥曲线,只是顶点移动至原曲线焦点且焦距变为ep/2。这些都是是中学数学啊。
细杆长度小于2ep则不能通过焦点,可以说明水平状态为唯一的平衡位置,即细杆重心在对称轴上。
下面以抛物线x2=2py为例,具体说明细杆重心轨迹及稳定平衡集。长L的细杆AB ,两端坐标满足

基于式(6) 绘出不同长度L细杆的重心轨迹(图3)。随着细杆长度的变短,重心轨迹极大值和极小值差异减小,在L=2p时即细杆水平通过焦点时三个极值点重合而成为单一最小值。
又,L<2p时右端式(6) 第一项大于1而第二项小于1,将在参数边界即xM=0达到最小值;否侧因两项乘积为常数而相等时达到极小值,有
 稳定平衡的重心轨迹为顶点在原抛物线焦点、焦距为p/2的抛物线以及 0~0.5p间对称轴;其上对称轴为不稳定平衡集。
稳定平衡的重心轨迹为顶点在原抛物线焦点、焦距为p/2的抛物线以及 0~0.5p间对称轴;其上对称轴为不稳定平衡集。
稳定平衡集在焦点处发生杈式分叉,即pitchfork bifurcation。
从图3看到,细杆较短可在光滑圆锥曲线内水平地稳定平衡;而其较长则要通过焦点而斜靠在壁面才能稳定——平正而居重心高呢。
1 徐 康. 圆锥曲线的静力学性质. 力学与实践,2014, 36(5):639-641
http://lxsj.cstam.org.cn/CN/abstract/abstract144681.shtml
2 尤明庆. 均匀细杆在光滑圆锥曲线壁内的稳定平衡分析. 力学与实践, 2016, 38(2): 186-188
http://lxsj.cstam.org.cn/CN/abstract/abstract145119.shtml
https://blog.sciencenet.cn/blog-275648-1065399.html
上一篇:对《论语•乡党》中三句话的解读
下一篇:戒盈杯:过犹不及话虹吸