几个月之前，接触到IEEE上一篇与自己的研究方向相关的论文，文章的思路非常的新颖，刚接触我就认为含金量应该非常高，所以我就尝试他的思路去重复其结果，然后在利用其思路去研究其它的东西。

  这篇论文是一位国外学者所写，在这里就不说明具体是哪位学者的哪篇文章，仅仅粗略的描述一下情况，希望大家见谅！我相信有看过这篇文章的老师应该从我的描述能有所印象。

  首先，这篇文章是求一种材料的电导率，这是通过matlab编程得出数值解，在其它的参数固定下，画出其随频率的变化曲线。然后，通过一种新的方法去拟合相同条件下的电导率实部与频率的曲线图，与数值解所求的结果进行比较。

 其文章中的图，离散点是拟合的点，连续曲线是数值解：

可以看出文中给出的两种方法求得的结果图高度接近，拟合程度非常的好，这就证明了其采用一种新的方法的可靠性得到了保证。

 那么，看到这样的结果后，我也就开始步上重复其所做的工作。他的创新方法具体是：先根据matlab编程计算出具体的数值解，然后利用该文章（E. C. Levi,“Complex-curve fitting,” IRE Trans.Autom. Control, vol.4, no. 1, pp.37–44, May 1959.)中的相应数学方法，对matlab编程所求的电导率值进行采样，取得若干个电导率值，然后将其分别进行归类于实部与虚部。进行矩阵变换，得到所求的矩阵系数，即将所给的电导率表达式写成{（A0+A1(jw）+A2（jw)+......An（jw）/B0+B1(jw）+B2（jw）+.......+Bn（jw）}的形式，它的系数A_i、B_i就是利用前面的矩阵变换得到，再将求得的系数A_i、B_i代入matlab中的留数函数residues中，求得到其零极点p_k、r_k，最后将得到的零极点代入文章中的另外一组公式：

其中：p_k、r_k 为上面求得的零极点，上式求得的ρ_k（w）为电导率的倒数

这样就通过拟合的方式求得求得不同频率下的电导率，进而可以画出其实部与频率的曲线图。

1.      我通过matlab编程得到数值解的电导率实部与频率的关系图与其上图实线的结果一致：

1.      然后就是：利用该文章（E. C. Levi,“Complex-curve fitting,” IRE Trans.Autom. Control, vol.4, no. 1, pp.37–44, May 1959.)中的相应数学方法，采样，最终求得零极点p_k、r_k

2.      论文作者求得的p_k、r_k是：

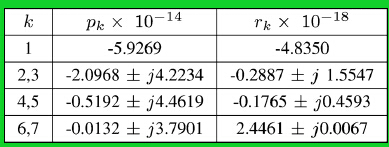
ρ_∞=1.6794 e+04

但是我求得结果是；

r =

  1.0e+18 *

-4.772853442852258                    

-0.301058332130681 + 1.551265765034745i

-0.301058332130681 - 1.551265765034747i

-0.179352445668960 + 0.460192679656625i

-0.179352445668961 - 0.460192679656625i

 2.446229085749384 + 0.006925474060592i

 2.446229085749386 - 0.006925474060589i

p =

  1.0e+14 *

-5.881146116947460                    

-2.098690413144979 + 4.209799343171316i

-2.098690413144979 - 4.209799343171316i

-0.519774157644342 + 4.460597491796755i

-0.519774157644342 - 4.460597491796755i

-0.013184730879960 + 3.790064061124983i

-0.013184730879960 - 3.790064061124983i

ρ_∞  

     = 1.678170850183442e+04

可以看出来我计算得到的结果与其结果在具体的数值上非常接近（有一点差异是因为采样的点可能不同、个数可能不同），但是数量级刚好相反，

他的p_k是1.0e-14、r_k是1.0e-18；

我的是：p_k是1.0e+14  、r_k是1.0e+18；

在这里可以几乎肯定是他的数量级是不对的，因为这里所取的频率都是在太赫兹下进行的即w=2*п*f （f是从1THz到100THz），那么根据上面的公式有，则需要有p_k的数量级应该与w是匹配的，而且我的结果最后求的电导率的结果与数值解求得的结果的数量级是一致的，若采用作者的数据就无法得到，而且论文中给出了的ρ_∞值与我计算得到的值是一致的，所以此处认为是其书写上的错误。

4．那么最后一步就是：把零极点p_k、r_k ，代入上面的公式中，得到电导率，在画出拟合后的电导率实部与频率的曲线图，他的图在上面看到是很好的拟合，而我的图却是这样的：

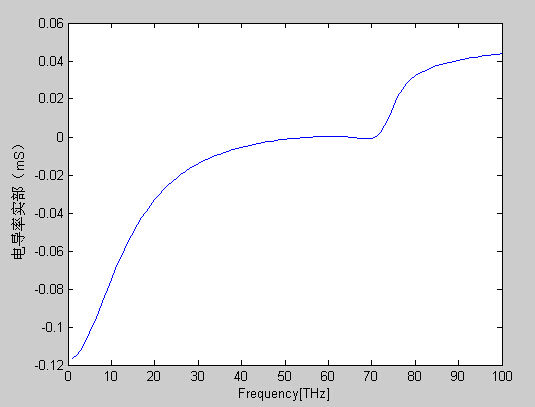
根本就无法得到，如果文章的方法是正确的，在我求出零极点后，代入最后的公式那就很简单的一步了，我的最后代码检查了很多遍，没发现问题，让其他的研究人员也复核过，也没有发现问题，如果我采用论文的零极点数据代入公式得到的图形是这样：

这个问题我纠结很久，最终还是没得到解答，于是我在四月底，邮件联系了作者，同时也把我的拟合代码发了过去，但过了一个多月后，他仍没给我回复；到六月中旬的时候，我又发了一封邮件，这次作者很快就回复我了，他的回复如下：I just received your email. Your last email mightgo in the spam box. I'll write to you soon (by a couple of days.)，后来等了十几天还是没回复，我在六月下旬又联系了作者，这次又很快回复了，他的回复如下：Hi，I am so sorry. I will answer your questions bythis week.

    现在眼看7月下旬都快要到了，仍然还是没有回复，我也不打算再去询问作者了，但是在这里很是不解——为什么会出现这样的情况？我的问题究竟是出在哪里了呢？