博文
同样都是鸾尾花iris数据,为什么PCA图相反?
|
PCA简介
主成分分析(principle component analysis)是一种线性降维方法。它利用正交变换对一系列可能相关的变量的观测值进行线性变换,从而投影为一系列线性不相关变量的值,这些不相关变量称为主成分(Principal Components)。PCA是一种对数据进行简化分析的技术,可以有效地找出数据中最“主要”的元素和结构,去除噪音和冗余,将原有的复杂数据降维,揭示隐藏在复杂数据背后的简单结构。
网络上的两种不同结果
使用鸾尾花(iris)数据进行PCA分析时,相同的数据,在网上会有两种不同的结果图。
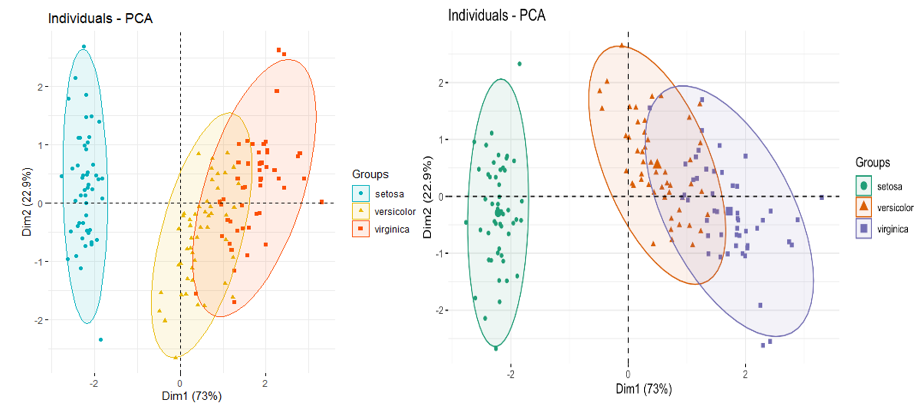
仔细看会发现,这两个图的X轴是一样的,Y轴反了。
这是怎么回事,到底哪个是对的?
PCA绘图代码1
library("FactoMineR")
library("factoextra")
data(iris)
iris.pca <- PCA(iris[,-5], graph = F)
fviz_pca_ind(iris.pca,
geom.ind = "point", # show points only (nbut not "text")
col.ind = iris$Species, # color by groups
palette = c("#00AFBB", "#E7B800", "#FC4E07"),
addEllipses = TRUE, # Concentration ellipses
legend.title = "Groups")
绘图代码2:
library(ggplot2)
data(iris)
iris.pca <- prcomp(iris[,-5], scale=T)
df_pcs <-data.frame(iris.pca$x, Species = iris$Species)
ggplot(df_pcs,aes(x=PC1,y=PC2,color = Species))+ geom_point()+stat_ellipse(level = 0.95, show.legend = F)
在R中运行后,出的图确实是相反的。经过对比,发现计算PCA时用的函数不一样,一个是iris.pca <- PCA(iris[,-5], graph = F)(默认scale);一个是iris.pca <- prcomp(iris[,-5], scale=T)。问题就出在这里。
经过检索,在stackexchange上有人回答了这个问题。
A PCA decomposition maps the original variables into new dimensions which capture the highest amount of variability. Note that the directionality of these dimensions is completely irrelevant - given a dimension that captures some amount of variability,
the negation of that dimension also captures the exact same amount of variability.
Because of this, the positive/negative direction of a PCA dimension may be arbitrarily chosen. Different software packages may produce different results depending on how they are coded, and slight variations in the input data could also result in a near-identical but flipped PCA plot.
也就是说不同的软件包/函数,包括:prcomp()和princomp() [R内置stat包]、
PCA() [FactoMineR包]、dudi.pca() [ade4包]、epPCA() [ExPosition包]和ggbiplot[ggbiplot包]等,它们的结果会依赖于代码、平台(linux、windows、mac),及输入数据的微小变化,产生几乎一样但是翻转的(flipped)PCA结果。
感兴趣的小伙伴可以带入代码试试看。
微生信助力高分文章,用户98000+,引用1500+
https://blog.sciencenet.cn/blog-707141-1392394.html
上一篇:为什么上传GEO前需要校验fastq文件正确性,并使用md5值验证文件完整性?
下一篇:根据蛋白质序列,计算其分子量(molecular weight),在线工具,原理和python代码