当前，贝叶斯统计越来越流行，在主流学术期刊统计分析中的应用愈发猖狂。相对于传统频率统计，贝叶斯统计有一些独到的优势，比如可以在模型中加入根据已有知识得来的先验分布，对参数不确定性的描述更符合逻辑，模型可以更为复杂等等。但今天，给大家介绍一下贝叶斯统计中的一个独门优势，那就是可以依据模型参数估计的结果，进行二次运算，这个是频率统计无法做到的，这种二次运算可以帮我们定量的回答很多问题。

废话不多说，上一个案例。假如我们有个数据epilepsy，数据结构如下：

如果目前我们的目的是要分析Age, Base和Trt这三个变量对count的影响，这里因为Age和Base都是数值型变量。为了使其对count的影响直接可以比，我们就把二者分别标准化（mean=0, SD=1）, 也就是得到了zAge和zBase这两个变量。当然，仔细观察这个数据的话，还会发现它有明显的的嵌套结构（有来自不同patient的数据），且count为计数数据，所以广义线性混合模型对这个数据最为合适。但现在我们不管它，我们就用最简单的线性回归来处理它。那么我们拟合以下模型：

我们会看到，Age和Base对count均有显著影响，且Base的影响程度明显更大。但现在，如果问你，Base对count的影响到底比Age对count的影响大多少呢?

你可以笼统的用9.6306/1.1469=8.3971来回答，也就是Base对count的影响大概是Age对Count的影响的8倍。

但事实上，在统计中，单单一个估计值能提供的信息是有限的，我们往往还需要这个估计值的置信区间，才能令人信服。但上述案例中，8.3971的置信区间，或者误差范围是多少呢？在频率统计中，我们是无法得到这个值的置信区间的，因为频率统计是点估计。

但是在贝叶斯中，由于我们得到的所有结果都是一组后验分布，我们就可以依据参数的后验分布进行各种我们需要的二次运算，并轻松得到二次运算结果的置信区间。以上述案例为例，我们拟合一个贝叶斯线性回归模型：

library(brms)

m2 <- brm(count ~ zAge + zBase + Trt,data = epilepsy)

这里我们为了简洁和易于理解，一切其他贝叶斯设置都采用默认设置，一样可以得到收敛完好的结果。

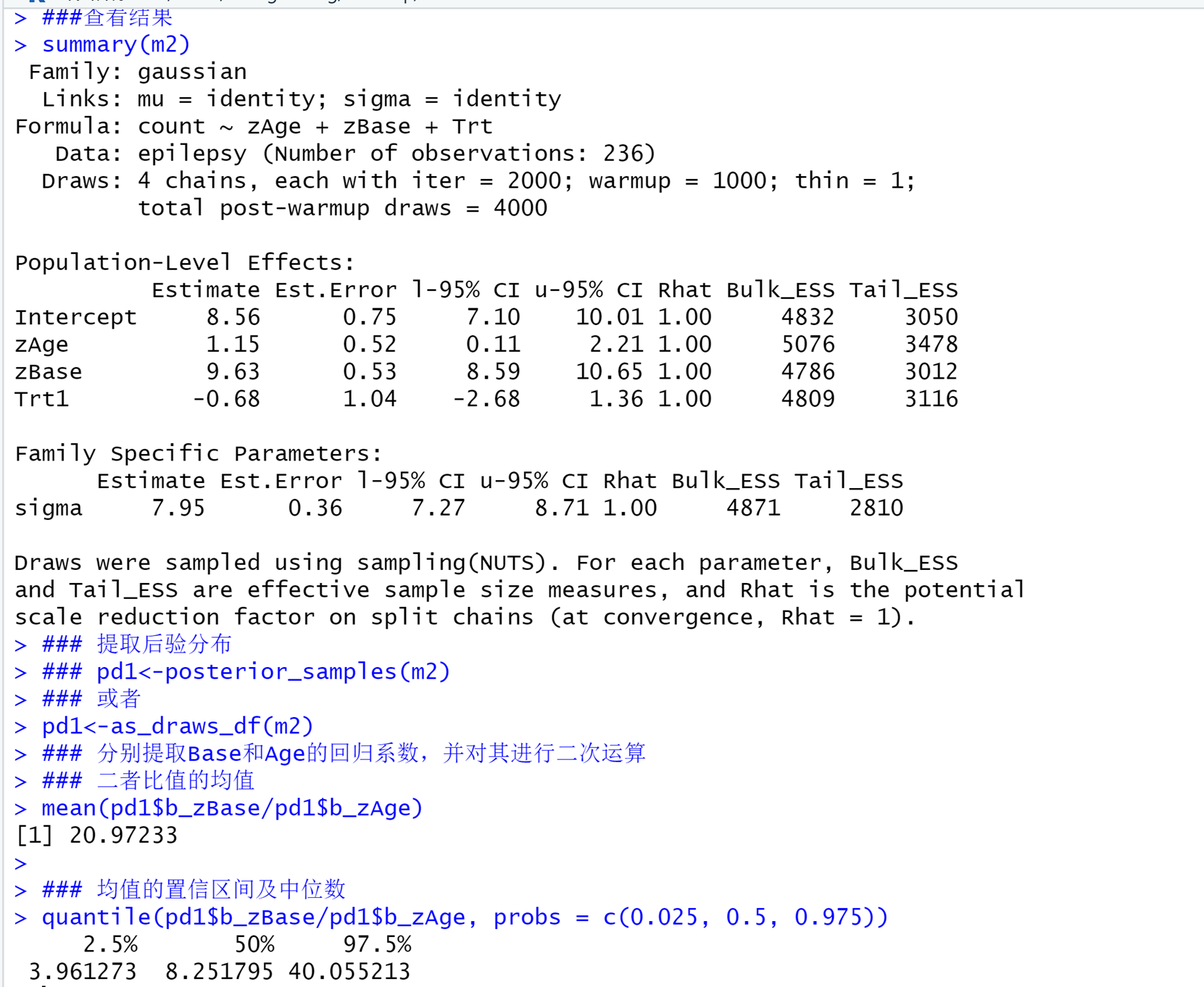
可见，和频率统计中只能给出一个参数的比值不同，贝叶斯模型中，平均来说Base对count的影响是Age对count的影响的大约21倍，中位数是8.25倍，95%分位数为3.96-40.05倍。这个结果，就更加定量化的告诉我们，Base对count的影响是远远的大于Age对count的影响的。这样，我们就可以采用贝叶斯统计来回答很多频率统计里面无法回答的参数大小对比问题了。