博文
[转载]several blocks of Deep learning
|||
Deep learning is like a black box. Its learning process takes the inputs and the desired outputs, and then updates its internal states, so that the calculated outputs get as close as possible from the desired output. So machine learning sometimes is called model fitting.
Decompose the learning process into several building blocks:
Step 1 --Model Initialisation
The first step of the learning, is to start from somewhere: the initial hypothesis. A random initialisation of the model is a common practice.
The rational behind is that from wherever we start, if we are perseverant enough and through an iterative learning process, we can reach the pseudo-ideal model.
Step 2--Forward propagation
Pass the input through the network layer and calculate the actual output of the model straightforwardly.
Step 3--Loss function
absolute loss, square loss, sum of square loss
The most intuitive loss function is simply loss = (Desired output — actual output). However this loss function returns positive values when the network undershoot (prediction < desired output), and negative values when the network overshoot (prediction > desired output). If we want the loss function to reflect an absolute error on the performance regardless if it’s overshooting or undershooting we can define it as:
loss = Absolute value of (desired — actual ).
If we go back to our football player example, if our newbie guy shoots the ball 10m to the right or 10m to the left of the goal, we consider, in both cases, that he missed its target by 10m regardless the direction (right or left).
In this case, we will add a new column to the table -> the absolute error.
However, several situations can lead to the same total sum of errors: for instance, lots of small errors or few big errors can sum up exactly to the same total amount of error. Since we would like the prediction to work under any situation, it is more preferable to have a distribution of lots of small errors, rather than a few big ones.
In order to encourage the NN to converge to such situation, we can define the loss function to be the sum of squares of the absolute errors (which is the most famous loss function in NN). This way, small errors are counted much less than large errors! (the square of 2 is 4, but the square of 10 is 100! So an error of 10, is penalised 25 times more than an error of 2 — not only 5 times!)
Notice, if we consider only one case, we can somehow say that the network predicted correctly the result. However, this is just the beginner's luck, like our football player analogy who can manage to score from the first shoot as well. What we care about is to minimize the overall error over the whole dataset (total of the sum of the squares of errors!)
Simply speaking, the machine learning goal becomes then to minimize the loss function (to reach as close as possible to 0).
We can just transform our machine learning problem now to an optimization process that aims to minimize this loss function.
Step 4--Differentiation
The optimization technique is to modify the internal weights of neural networks in order to minimize the total loss function. So, is there any relation between model weights and loss functions? --The answer is YES, and the relationship is indirect.
As displayed in the example of the raw blog (https://medium.com/datathings/neural-networks-and-backpropagation-explained-in-a-simple-way-f540a3611f5e), weights' change has direct relations with the loss change which can utilize the derivative of the loss function to describe. Like the following descriptions:
-If the derivative is negative, meaning the error decreases if we increase the weights, then we should decrease the weights.
-If the derivative is negative, meaning the error decreases if we increase the weights, then we should increase the weights.
-If the derivative is 0, we do nothing, we reach our stable point.
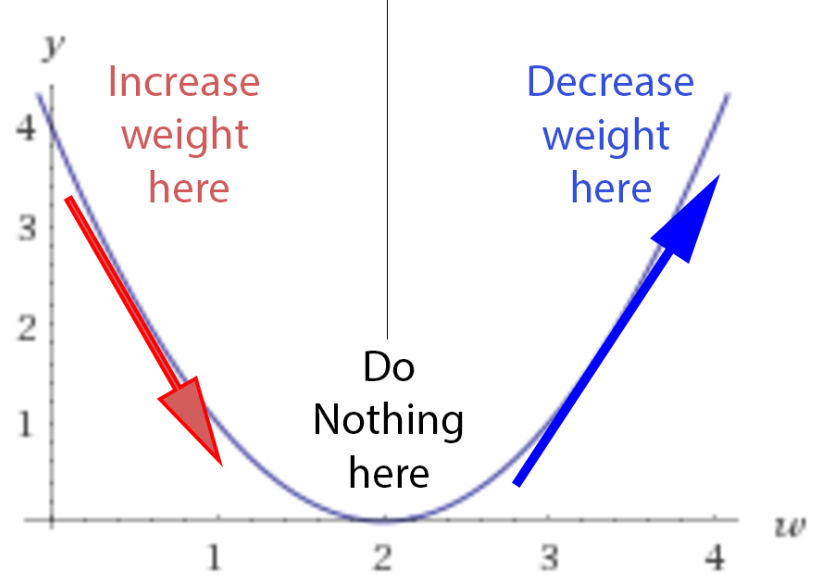
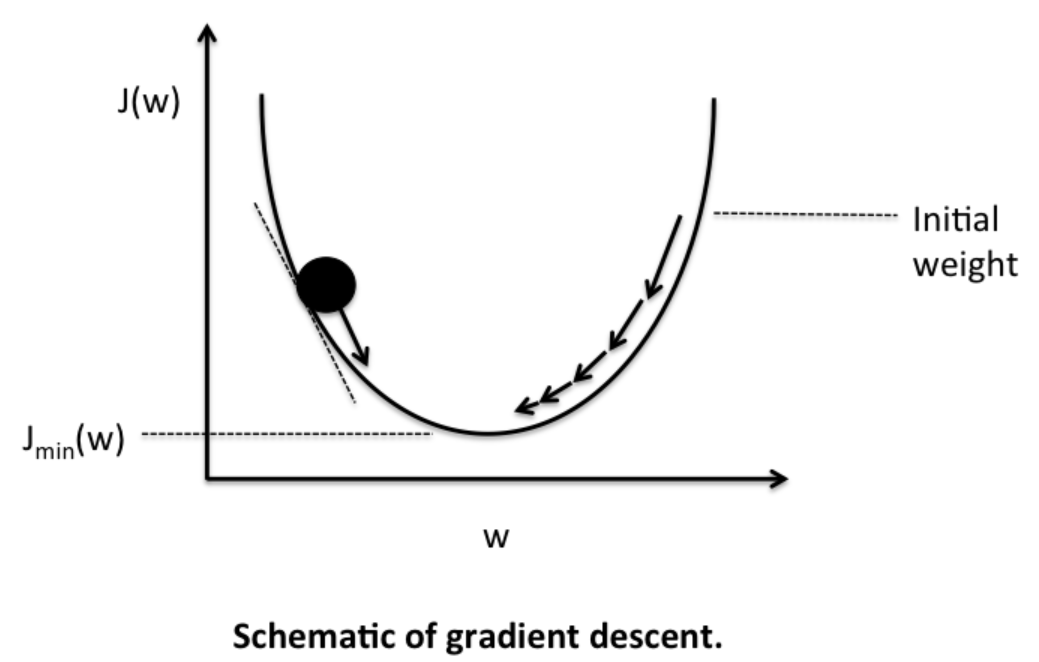
Their relationship acts like gravity. No matter where we randomly initialize the ball on this loss function curve, there is a kind of force field that drives the ball back to the lowest energy level of ground 0.
Step 5--Back-propagation
Generally, a neural network has multiple layers. We need to calculate the derivative of every layer. Luckily for us, the derivative of layers is decomposable, thus can be back-propagated.
We have the starting point of errors, which is the loss function, and we know how to derivative it, and if we know how to derivate each function from the layers, we can propagate back the error from the end to the start.
In other words, if we create a library of differentiable functions or layers where for each function we know how to forward-propagate (by directly applying the function) and how to back-propagate (by knowing the derivative of the function), we can compose any complex neural network. We only need to keep a stack of the function calls during the forward pass and their parameters, in order to know the way back to backpropagate the errors using the derivatives of these functions. (This technique is called auto-differentiation)
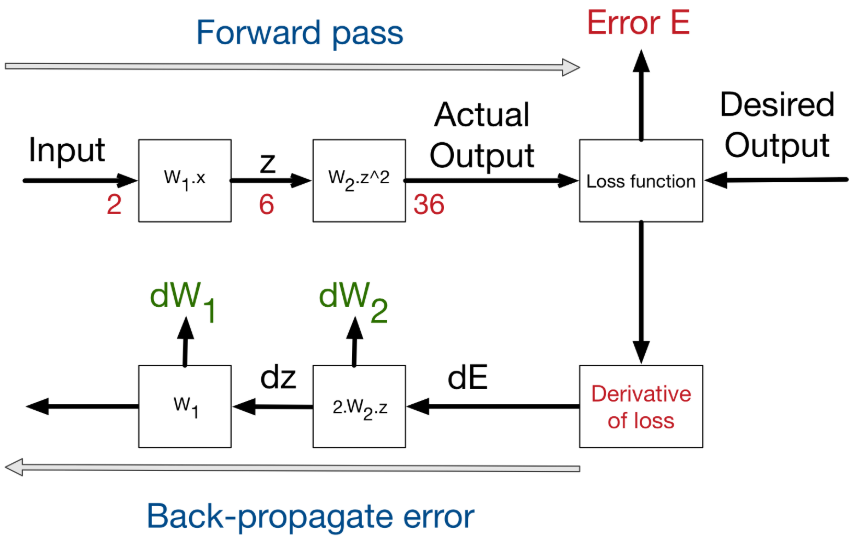
This figure shows the process of backpropagating errors following the schemas:
Input->Forward calls->Loss function->derivative->back-propagation of errors.
At each stage, we get the delta on the weights of the stage.
Step 6--Weight update
As we presented earlier, the derivative is just the rate of which the error changes relatively to the weight changes.
However, as described in the example of the raw blog, for real-life problems, we shouldn't update the weights with such big steps. Since there are lots of non-linearities, any big change in weights will lead to chaotic behaviour. And, we shouldn't forget that the derivative is only local at the point where we are calculating the derivative.
Thus, the general rule of weight updates is the delta rule:
New weight = old weight - derivative rate * learning rate
The learning rate is introduced as a constant (usually very small), in order to force the weight to get updated very smoothly and slowly (to avoid big steps and chaotic behavior).
Now, several weight update methods exist. These methods are often called optimizers. The delta rule is the most simple and intuitive one, however, it has several drawbacks.
There are 3 optimization modes: full online (i.e., N=1. e.g., SGD)/mini-batch/full-batch.
Step 7--Iterate until convergence
In neural networks, after each iteration, the gradient descent force updates the weights towards less and less global loss function. That is, the weight update is guided by decreasing loss, and thus is smart.
How many iterations are needed to converge?
* This depends on how strong the learning rate we are applying. High learning rate means faster learning, but with higher chance of instability.
* It depends as well on the meta-parameters of the network (how many layers, how complex the non-linear functions are). The more it has variables, the more it takes time to converge, but the higher precision it can reach.
* It depends on the optimization method used, some weight updates rule are proven to be faster than others. (From the following figure, we know SGD is prone to local optimal, but it may reach the global optimal with the Momentum)
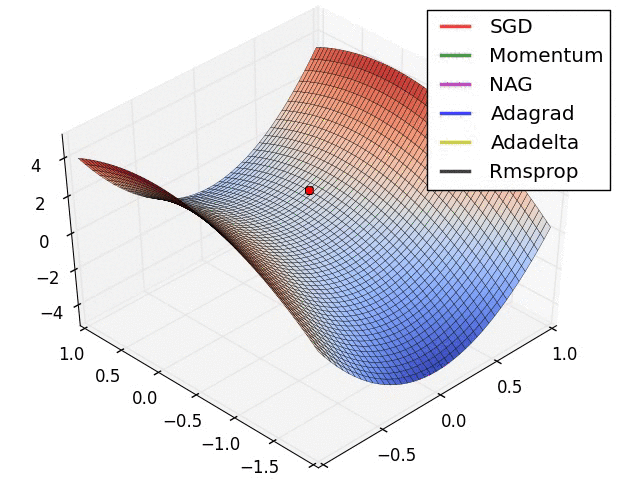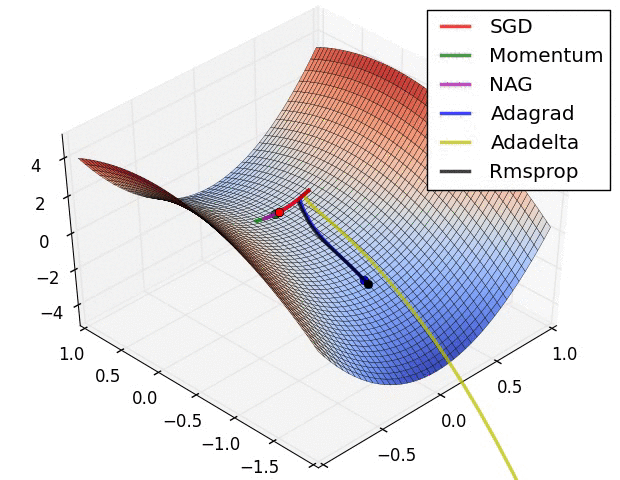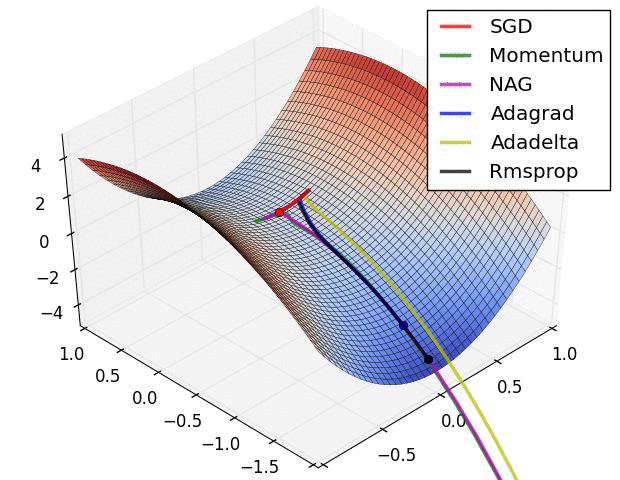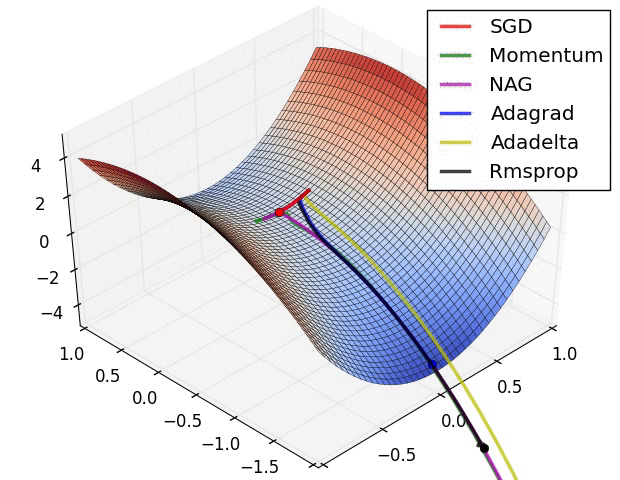
* It depends on the random initialization of the network.
* It depends on the quality of the training set. If the input and output has no correlation between each other, the NNs will not do magic and can't learn a random correlation.
Overall pictures
In summary, here is what the learning process on NNs looks like:
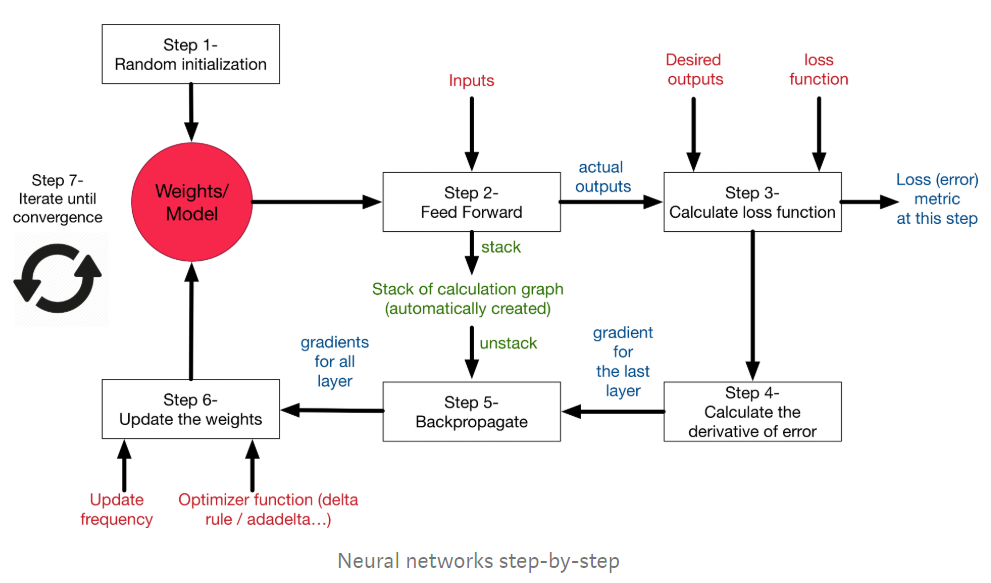
https://blog.sciencenet.cn/blog-1969089-1194797.html
上一篇:[转载]Pytorch可视化过程之tensorboardX的使用
下一篇:使用plotly在线显示3D可交互图像
全部作者的其他最新博文
全部精选博文导读
相关博文
- • 热烈祝贺海南大学9位学者入选斯坦福大学顶尖科学家2024年Career榜
- • 祝贺访问学者吕改芳和研究生杨梦蝶等合作SCI论文在Colloids and Surfaces A发表
- • Relativity of Hallucination(初学者版)
- • Are Human Beings Living in a Hallucination?(初学者版)
- • Theory of Relativity of Hallucination by Yucong Duan(初学者版)
- • The "Emergence" of LLMs by Relativity of Consciousness(初学者版)