地球系统力学动力学（4）

李务伦

吉林省煤田地质局二零三勘探队

第四部分  球内合力强度方程及作用

这一部分以建立球内合力强度方程为主线，分以下步骤：1、讨论均匀球自转球内合力强度方程；2、讨论外部平行引力场与自转均匀球内合力强度方程；3、讨论外部周期性引力场与自转均匀球内合力强度方程；4、总结出球内性质Ⅲ；5、利用球内方程解释一些地球动力学出现的韵律问题。

1、引言

旋转的地球和旋转的碎屑组成的Ryugu和Bennu小行星，都为椭球体；旋转的地球具有引力潮；地球具有构造韵律等。该如何从理论上解决，下面通过建立球内方程一一解决！对于地球为椭球体，牛顿和惠更斯指出：由于地球自转离心力，地球是旋转椭球体。对地球是旋转椭球体这一形态地球物理学家用球谐方程给出了解释。许多著作可以查到，不做赘述。但面对以下的事实，并没有检索到相应的理论上给予解释。地球是太阳系的成员，太阳系是银河系的成员。太阳系穿越银道面的周期是30～35Ma左右。在地球穿越银道面时，根据万天丰教授的研究，陨击撞击地球，与地球穿越银道面时间相合^[1]；还有学者对地质事件与穿越银道面做了研究，研究表明地球各圈层主要地质事件的旋回周期如表4-1和图4-1所示^[2]35-36。

另外，马宗晋系统性地将地球构造活动韵律性做了详细研究，并划分出了长韵律、中韵律、短韵律和微韵律4个层次,12个韵律级别，详情见表4-2^[2]。由此可见地球形态及周期性的构造规律不可不重视，而该如何解释这些规律？从何处下手解释这些规律？下面从球内方程给出解答。 

图4-1  地史上35Ma左右的重要地质事件集中期与穿越银道面时间对比 

2、旋转均质球内的力强度方程^[3]

如图4-2所示，太空中球均质，半径为R，密度为ρ，旋转角速度为ω。A为球内任意一点，距球心距离为r，该点的引力强度（大球引力强度）为式：

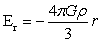…（4-1）

A点处单位质点离心力为：

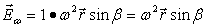…（4-2）

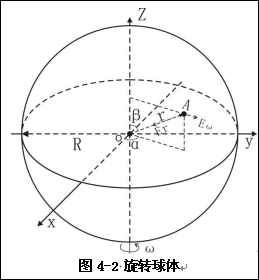
单位质点离心力，也可以看做是离心力强度，这样一来与引力强度就统一起来，进而可以将式（4-1）和式（4-2）投影到图4-2的各坐标轴上：

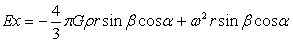…（4-3）

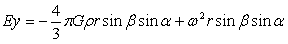…（4-4）

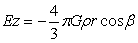…（4-5）

由式（4-3）到（4-5）得引力强度、离心力强度之合力强度为：

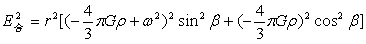…（4-6）

椭球为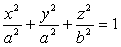（a＞b）的极坐标方程为：

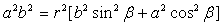…（4-7）

对比（4-6）、（4-7）两式可以发现合力强度方程（4-6）也为椭球方程。如果球物质黏度低，图4-2内质点将依合力强度方程（4-6）运移，运移的结果，图4-2正球形变为椭球形。对于含球层球中，任意球层的如图4-2任意点A，其合力强度方程也为式（4-6）。所以含球层的自转的地球为椭球形也就好理解了。

为了使方程（4-6）更具有一般性和普遍性，将密度随半径具有ρ=ρ(r)变化的球内强度换成式（3-16），于是就有了如下强度公式：

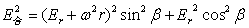
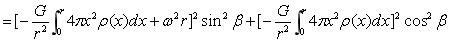
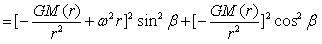…（4-8）

显然（4-8）这一方程仍为扁椭球方程。有了这一方程，对于前述的球层虽也可以求出类似的方程，但在解觉具体问题上，意义并不是太大，故而不做过多的讨论。但对于角速度存在周期性变化的情况，（4-6）、（4-8）所表达的球内合力强度也存在交变。

通过上面的推理知，式（4-6,4-8）椭球方程可用向量方程表述上述为：

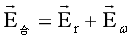…（A1）

当自转角速度具有周期性，合力强度式（A1）也具有周期性。

球内合力强度方程的得出后，自然会提出球内合力强度线是否还是直线方程？下面通过计算给出球内合力强度线方程。根据方程（4-3）、（4-4）、（4-5）可得到如下方程：

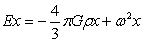
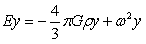
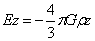
将此方程带入微分方程dx/A_x=dy/A_y=dz/A_z，于是有：

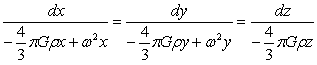，解该方程得如下合力强度线方程：

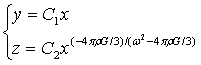…（4-9）

从（4-9）式可以看出，球内合力强度引力线不再是直线，而是过球心的曲线，且垂直等合力强度椭球面。

对于球内合力强度（4-8），球内合力强度线与（4-9）类似，由于与今后要解决的问题意义不大，故不再解出。只要知道球内合力强度线为曲线，且通过球心即可。需要特别强调的是：无论球体多么大，球表面合力强度线，无论相距多近，始终存在一个夹角，即球表面不存在平行引力强度线，时下教科书平行力线的提法，不过是科学家为利于质点力学问题的方便解决，而进行的假设而已。

由（4-6）或（4-8）求出等强度面、等压力面和等位面方程。等强度面、等压力面和等位面方程为椭球面，而这些方程只不过比正球形和含球层的正球形稍有复杂，与要解决的问题并非重要，故不再求出。同椭球面上引力强度值、压力值、位能值处处相等，强度线垂直椭球面。前述的球内性质Ⅱ1-7仍然成立，只不过正球面换成了椭球面，合力强度力线由直线换成了曲线。

下面对地球赤道的引力强度和离心力强度进行对比，引力强度和离心力强度之比为E_r/E_ω=4πGρr/3/(ω²rsinβ），当β=90o，E_r/E_ω=4πGρ/3/ω²。对于地球而言，可用该式进行粗估。地球平均密度5500kg/m³,角速度为2π/(24×3600)弧度/s,所以E_r/E_ω≈292。但地球密度由内而外有大变小，E_r/E_ω也有大变小。尽管引力强度远大于离心力强度，如此小的离心力强度确造成地球长轴为6378.137km，短轴6356.752km，两者相差11.385km。

研究表明，地球自转存在长期的减速和较长尺度的长周期变化^[4]，因此角速度是时间的周期性递减函数，所以地球内的合力强度也是时间的周期性函数。所以等压力、等位能、等强度椭球面，也将周期性改变，这就为离极力，柯氏力形成地质作用提供了基础，因此地球自转与大的地质构造有着千丝万缕联系。经向纬向构造带的形成，于这种周期性变化自然脱不了关系，但是否能引起大陆漂移，能否引起大陆分裂聚合，将在后面讨论。

3、恒定平行引力场对旋转球体的影响^[3]

如图4-3中均匀引力场强度E=E(y)是一与y轴有关的单值函数，力线平行于y轴，且随y的变化而变化，均匀球内A点在三轴中的引力强度如下：

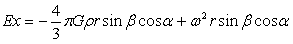…（4-10）

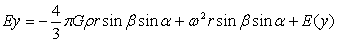…（4-11）

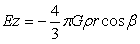…（4-12）

（4-10）、（4-11）、（4-12）合引力强度为

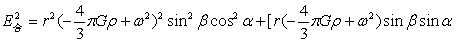
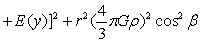…（4-13）

椭球为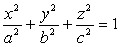（a≠b≠c）的极坐标方程为：

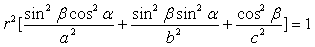…（4-14）

对比（4-13）、（4-14）两式，（4-13）也为椭球方程。

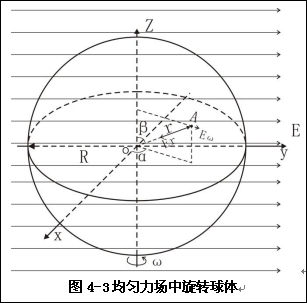
在式（4-13）中角速度恒定，正球形成为稳定的椭球，而当E=E(y)周期性变化时，合力强度也将周期性变化；内部等压力、等位能、等引力强度椭球面，也将周期性改变。

同样为了使方程（4-14）更具有一般性和普遍性，将具有密度随半径变化，即ρ=ρ(r)的球内强度换成式（3-16），于是就有了如下球内合力强度公式：

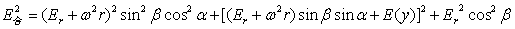
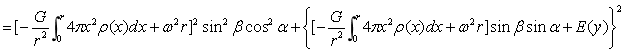
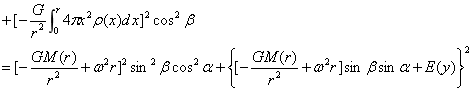
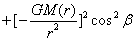…（4-15）

通过上面的推理知，式（4-13,4-15）椭球方程可用向量方程表述上述为：

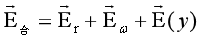…（A2）

当自转角速度具有周期性，恒量的引力场的加入，也不会改变合力强度也具有周期性。

5、一般情况下处于外力场中旋转球体的球内性质总结^[3]

根据（4-17）到（4-19）可以求出合力强度线方程，合力强度线为曲线的方程；也可以求出球内任意一点压力、位能；以及等压力面、等位能面、等强度面方程。前面已述具体的方程与要分析的问题意义不大，只要前述性质1-7中，引力强度换成合力强度，直线换成曲线，正球形换成椭球形，7条性质仍然成立。为方便应用，表述如下：

性质1：椭球球内任意点合力强度线为曲线，所有合力强度线止于球心，除椭球心外，任意点合力强度线切线偏离椭球球心。

性质2：椭球球内等合力强度面、等压力面、等合力位面均为椭球形。

性质3：椭球内同椭球面上：引力强度值、引力位值、压力值处处相等。

性质4：椭球内同椭球面上，沿椭球面任意点引力强度、引力位、压力梯度横向各参数梯度为零；纵向上任意点上，各参数上梯度值相等。

性质5：椭球内引力线的切线与等引力强度面、等压力面、等引力位面垂直。

性质6：椭球内任一点的各向应力值与该点的压力值相等；

性质7：所有物质，由球心而外，按密度从大到小圈层展布。

性质8：椭球内所有质点具有动态平衡和周期性变化的特点。

为与前面球内性质Ⅰ、球内性质Ⅱ相区分，将上述总结出球内性质，称为球内性质Ⅲ。同时还需说明的是：在具有圈层的球内，单位体积的质量不同，旋转球体内的圈层，因密度的不同，又因自转和地外引力场的不同，所受的力并不相同，从而导致各圈层间出现摩擦，进而造成圈层间的旋转差异。因此上述方程从理论上解决了太空中真正存在形态的问题，及球内存在圈层间旋转的差异。这种圈层间旋转差异，杨学祥教授有下面的研究成果。

4、外力场中旋转球内部强度方程^[3]

上面分析了恒定平行外力场对旋转球体的影响，该稳定外力场的方向与Y轴平行。但事实是月球围绕地球周期性转动，行星围绕太阳周期性转动，太阳系在银河系一个悬臂上绕银心旋转的同时，还在银道面上下周期性运动。它们在地球的位置形成一个具有各种周期合引力场，因此可以定义一个随时间周期性变化的位于球内部外部合引力场强度之和函数：

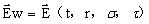…（4-16）

式中：t时间，r位于球内距球心距离，σ与Z轴夹角，τ在XY平面内与X轴夹角

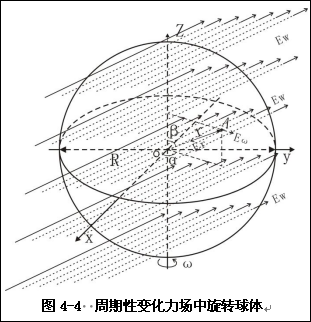
 根据月球对地球的引力强度线与地球相切的最大夹角不超过两度，其它星体对地球引力强度线与地球相切的夹角将更小，所形成的合引力强度线间角度将更小，所以可认为外力场场强线近于平行。月球在地球范围内的引力强度变化很小，因此可以认为外力场场强度在地球范围为恒值。而地外星体在地球处的引力强度具有周期性强度变化和方向变化的特征。于是假定合力强度具有以下特征：①在图4-4中，地外合力强度线平行；②在图示4-4中的球体范围内合力强度值不变；③存在多种周期。下面仍以均匀旋转球体计算图4-4中A点合力强度，其分合力强度如下：

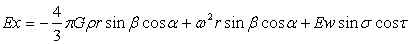…（4-17）

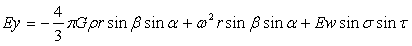…（4-18）

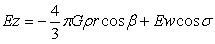………………………（4-19）

合强度为：

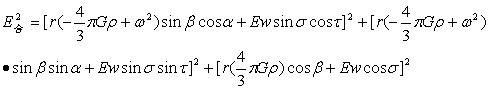…（4-20）

从方程(4-20)可以看出球内合力强度是一多元函数，由于Ew存在各种周期变化，所以E_合也存在相同的周期变化。根据方程（4-20）可知这也是一椭球方程，其等压力面，等位能面，等合力强度面也为三轴椭球面。同样为了使方程（4-20）更具有一般性和普遍性，将具有密度随半径变化，即ρ=ρ(r)的球内强度换成式（3-18），于是就有了如下强度公式：

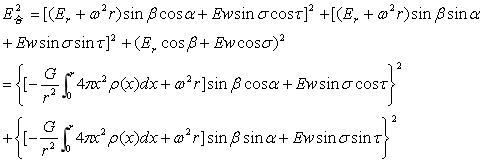
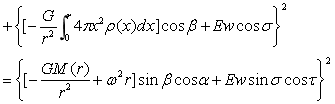
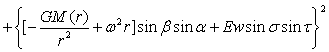
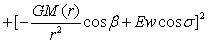…（4-21）

从以上（4-13）、（4-15）、（4-20）、（4-21）均为椭球方程，且根据这些方程，可求出它们的相应合力强度线，以及椭球内部等位面、等压力面，因与要解决的地质问题意义不大，故不再讨论。

通过上面的推理知，式（4-20,4-21）椭球方程可用向量方程表述上述为：

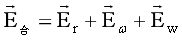…（A3）

当自转角速度具有周期性，外部引力场具有周期性，合力强度也具有各种周期性。

6、分异下形成圈层差异旋转理论

星云物质汇集成地球，最初是混沌并旋转着，并不存在目前的圈层。所有物质形成原始地球基础的同时，也建立属于原始地球的力学系统，并在这个力学系统中，依据均匀球内性质，根据上升力定理和下降力定理及圈层化定理，球内物质将发生迁移，即发生分异，并圈层化。球内物质迁移都又产生什么影响？下面依杨学祥老师的研究^[10]为基础做陈述。

（1）科氏效应与地球球内差异性旋转的形成

根据前面的位能讨论（第三部分附录），原始地球最初获得的最可能的位能是2.241×10³²J。这一位能有两方面的作用，一部分使得原始地球所有物质温度升高；一部分使得地球形成自转。至于这一位能多少使原始地球升温，多少使的原始地球旋转，时下没有相应的理论给出二者的具体分配，仅有“当地、月很近时，地球的自转速度比现在要快的多，周期大概为2-4小时^[11,79页]”作为参考。选地球最初的地球自转周期为2小时，最初的地球自转角速度为8.7267×10^-4rad/s；选地球最初的地球自转周期为4小时，最初的地球自转角速度为4.3633×10^-4rad/s。用以下公式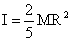：和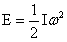（以上二式，I为转动惯量，M球的质量，R球的半径，E转动动能，ω为自转角速度）可求得平均密度5.52g/cm³时自转能前者为3.692×10³¹J，后者为9.232×10³⁰J。它们与引力位能2.24×10³²J的比值，前者为16.5%引力位能形成旋转能，后者4.0%引力位能形成旋转能，因此绝大部分使得原始地球升温。原始地球将升温，使得原始地球上的物质黏度降低，有利于原始地球不同密度的物质，在新形成系统力场下，根据浮力定理、上升力定理、下降力定理、浮力定理发生物质的分异，并根据圈层化定理和球内性质Ⅲ圈层化进行密度展布。下降和上升的质点在这新的力学系统中又将发生科氏效应，下面分析科氏效应带来的物理现象。

设在纬度φ处的点质量m与地心距离为R₁，由于地球以角速度ω自转。则点质量的东西向切线速度为：

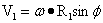…（4-22）

当同等点质量m距地心R₂时，且位于R₁上方或下方，点质量的东西向切线速度为：

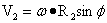…（4-23）

两者之间的速度差为：

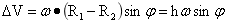…（4-24）

在式（4-24）中h=R₁-R₂。当h大于零，即当点质量m由远球心在下降力作用下向近球心运动，△V大于零，方向向东，点质量m偏东下降最后稳定；当h小于零，即当点质量m由近球心在上升力作用下向远球心运动，△V小于零，方向向西，点质量偏西上升最后稳定。无论是下降，还是上升，在这种过程中能量是守恒的。点质量m上升，由于△V小于零，途径圈层形成阻力，而使圈层旋转减速；点质量m下降，由于△V大于零，途径圈层形成助力，而使圈层旋转增速。因而造成球内原始地球形成中的球层出现旋转角速度的差异，且由内而外逐渐降低。这就是自转系统科氏效应，也就是地球内部存在差异性旋转的理论根据。上世九十年代初我国学者盖保民（1991）提出了岩石圈与核幔体之间的圈层差异旋转；马宗晋（1992）提出了岩石圈、地幔、与地核三者之间的差异旋转^{[12]前言1页}。1996年世界十大科技新闻之一，便是发现地球内核快速旋转^[12]。1994年6月杨学祥等根据经典物理理论证明地球内部各圈层间存在旋转差异^[13]，成果发表与1996年2月的“地球物理学进展”第11卷第一期上^[15]。

（2）地球内部差异旋转的宏观估算公式

地球各圈层的体积V_i、质量M_i、转动惯量I_i和自转动能E_i的表达式分别为：

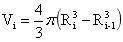…（4-25）

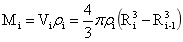…（4-26）

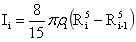…（4-27）

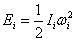…（4-28）

上述式中ρ_i，R_i和R_i-1、ω_i分别是各圈层的密度，内外半径和自转角速度，且R₀=0。在这些公式的基础上，讨论因重力分异，使旋转的地球内部因科氏效应造成圈层差异旋转的宏观估算公式。

对于均匀球体，转动惯量为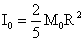：，对该转动惯量做如下变换：

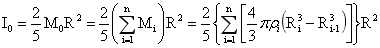
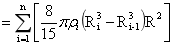…（4-29）

式（4-29）中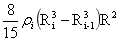也是一种转动惯量，它相当于质量为M_i的物质扩散到整个球时的转动惯量，定义为：

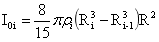…（4-30）

设均匀地球的转动惯量为I₀，自转角速度为ω₀，在重力作用下形成具有球层的旋转球体，由角动量守恒定律，在无外力作用的条件下有：

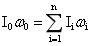…（4-31）

根据式（4-31）有：

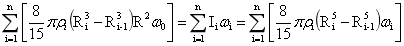…（4-32）

于是根据（4-32）可得出分异后各圈层角速度为：

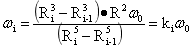…（4-33）

通过上面的推导证明了地球内部差异性旋转，并推出了科氏效应下，不同圈层理想差异性角速度的最大估算公式。事实上在物资的上、下位移的同时也因黏度出现角动量交换，角速度将再次统一，为了方便进行如下的方法计算。重力分异后各圈层通过角动量交换，角速度将再次统一为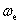后，根据角动量平衡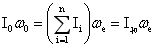有：

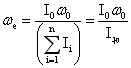…（4-34）

于是，经角动量交换再次统一后自转动能，简称为统一动能为：

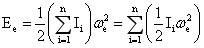…（4-35）

分层统一角速度自转动能，简称无差异旋转动能为：

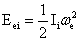…（4-36）

以上通过角动量守恒证明了地球内部各圈层间存在旋转差异，以及因黏度导致的全球的角速度再统一。

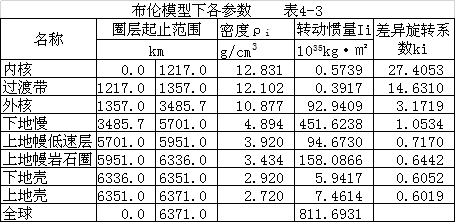
（3）各种参数的估算

表4-3依据布伦对地球内部构造的划分，计算了各圈层的转动惯量和圈层由于内部物质上升与下降造成的旋转差异系数。由计算数据可以看出物质的升降导致了地球内部由内而外，旋转速度以次减小，并且内核上升角速度较大，外部出现明显角速度明显降低，在中间部位出现角速度的不变带。下面在表4-3的基础上计算差异旋转能、无差异旋转能及层差异旋转能周期。

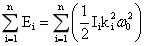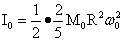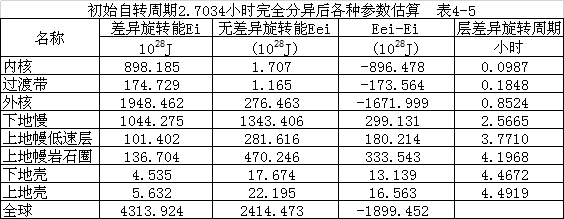
地球获得的最大总位能为2.470×10³²J，均匀地球的地球的重力位能绝对值为2.24×10³²J，两者相差2.293×10³¹J，该差能完全转变为地球内球层差异旋转能，根据式（4-26），（4-32）为：；而地球均匀自传能，由此二式得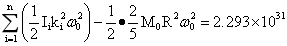。解该式ω₀=6.46×10^-4rad/s，而均匀自转周期为2.7034小时。下面就估算如下自转周期2小时，2.7034小时，4小时，在表4-3的参数下计算地球最初均匀旋转周期2、2.7034、4小时，估算差异旋转能，无差异旋转能及差异旋转周期和再次无差异旋转周期等。

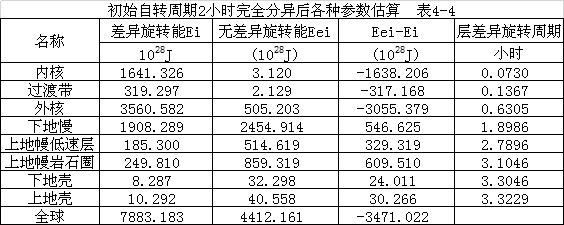
前面已计算出地球形成成后下降的最大的位能为：2.293×10³¹J。均匀地球自转周期为两小时，其自转动能为3.693×10³¹J，上述两者和为5.983×10³¹J，小于表4-4中差异旋转总能7.883×10³¹J。显然靠下降位能不足以引起这么大的差异旋转能，除非热能转化为旋转能。均匀地球自转周期为2.7034小时，下降位能，根据2.7034小时周期得出，下降的位能全部转为了差异旋转能。均匀地球自转周期为4小时，自转旋转能为0.923×10³¹J，它与下降位能2.293×10³¹J的和为3.216×10³¹J。这一数值与表4-6差异旋转能1.971×10³¹J相差1.245×10³¹J。这一值小于下降位能2.293×10³¹J，显然将有1.245×10³¹J的位能转变为热能。综上，以2.7034小时周期为界，小于2.7034小时为周期，要产生表4-4差异性旋转位能，需热能转换为旋转能；大于2.7034小时为周期，要产生表4-6差异性旋转位能，仅需部分下降位能即可实现，下降位能还要有剩余而转换为热能。

依据杨老师的模型，在表4-4到表4-6中，分别计算了差异旋转后，再次统一为同一自转周期后（此时满足方程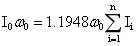），核部旋转周期变慢，向外输出能量，幔部和外壳旋转周期变快而获得能量，同时一部分核部输出的能量转变为热能。这一旋转能转变为热能，对核部保持高温无疑是有利的。

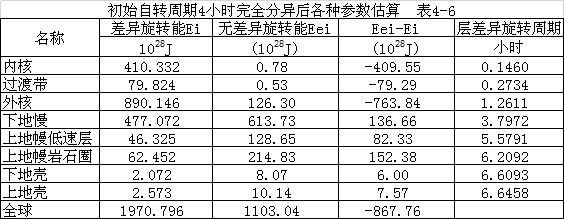
不同均匀地球初始周期，下降的位能导致球内出现差异性旋转，其旋转周期由内而外变大。但再次自转速度统一，由前述模型计算：初周期2小时，统一后周期1.6731；初周期2.7034小时，统一后周期2.2613；初周期4小时，统一后周期3.3504小时。

通过上面的分析，可以得到如下的结论：1、从理论上证明地球内部存在差异性旋转，证实地震数据发现地球内部存在差异性旋转合理性。2、根据模型的具体数据的估算，原始地球的自转周期不会小于2.7034小时。因为小于这一周期，需要另外的动力介入，方可实现依据上述模型得到差异性旋转。3、根据模型的计算，由差异性旋转到再次统一的自转周期，统一后的周期要小于初始周期，其佐证说明地球存在时快时慢的部分原因。

7、合力强度方程与构造韵律

有了合力强度方程，就可以解释一些构造现象，下面就结合具体问题应用这一方程。

7.1、自转与地球形态

地球赤道的引力强度和离心力强度之比为E_r/E_ω=4πGρr/3/(ω²rsinβ），当β=90o，E_r/E_ω=4πGρ/3/ω²。对于地球而言，可用该式进行粗估。地球平均密度5500kg/m³,角速度为2π/(24×3600)弧度/s,所以E_r/E_ω≈292(E_ω=0.03356m/s²)，但地球密度由内而外有大变小，E_r/E_ω也有大变小。

地球的形态，赤道半径大于两极半径，科学家们对此解释为地球的自转造成，他们的解释可在各种资料中见到，笔者不再赘述。下面用应用式（A1）解释。解释前先假定地球为定轴旋转，且无章动。由赤道向两侧，任意半径球面的点到定轴的距离逐渐减小，所以由赤道向两侧，任意半径球面的离心力强度有大到小。仅从球内压力来看，任意的球内半径球面上压力，由赤道向两侧由大到小。从而造成压力的不再平衡，并且赤道压力减小最多，形成低压区，两侧可塑物质将有两极向赤道方向汇聚，以建立新的平衡，当新的平衡建立后，就造成赤道半径大于两极半径，因而地球形成椭球体。

这一运动作用于高粘度的物质，然后被封存，就形成地质的一种构造韵律。

7.2、离极力不可能造成大陆漂移

离极力引起大陆漂移最初由魏格纳提出，后李四光前辈发扬这一思想，提出大陆阀学说，以解释大陆漂移。科学的研究发现地球自转忽快忽慢，具有一定周期性，这也就成了李四光老前辈理论的主要基础。然随着研究深入，1979年，王仁院士计算地球自转速度变化，引起的构造应力值仅为几个帕；这与实测构造应力值都在几十到上百吉帕，相去甚远。地球自转的作用虽没淡出人们的视野，但笔者在此认为其作用确开始回归理性。

对此，滕吉文等在论述这一学说时指出^[5]：“应当看到地球自转假说有一定的合理内核，但对陆内造山、成盆及其耦合响应，地震与火山的形成等一系列巨型构造体系，特别是其深层动力过程和物质能量的交换尚难以给出理念和解释。因为地球自转假说所涉及的仅为地球的浅表层过程，而在地球动力学研究与探索中，其深层动力过程是主要的”。

1990年，Doglioni^[2]44页根据世界不同地区板块运动方向的资料，绘制了软流圈向东流动和板块朝西运动的流线图4-5，用来说明岩石圈与软流圈相对运动结果。图中流线走向与主要板块运动方向一致。裂谷与挤压带大致与流线垂直，张扭或压扭地区与流线的总走向斜交。新生带裂谷带的伸长轴和山链的缩短轴与全球流线一致。流线的全球性大起伏可能是由于地球自转轴的不稳定摇摆（章动）引起的。在向西运动的岩石圈和向东运动的软流圈之间存在一滑脱带，其深度与软流圈顶部的低速带一致。在完全由大洋岩石组成的太平洋板块之下，低速带非常发育，岩石圈与软流圈之间去耦强烈；古老的大陆地盾，低速带不明显，去耦作用很弱。岩石圈和软流圈之间去耦作用的差异，可以解释所观察到的板块边界的变形。正是由于在这个全球性滑脱面上板块有不同的速度，才产生了板块之间的分离和碰撞，否则这个系统就是固定不动的。除了上地幔低速层这个主滑脱面外，在地壳底部和下地壳内还可能存在滑脱面。

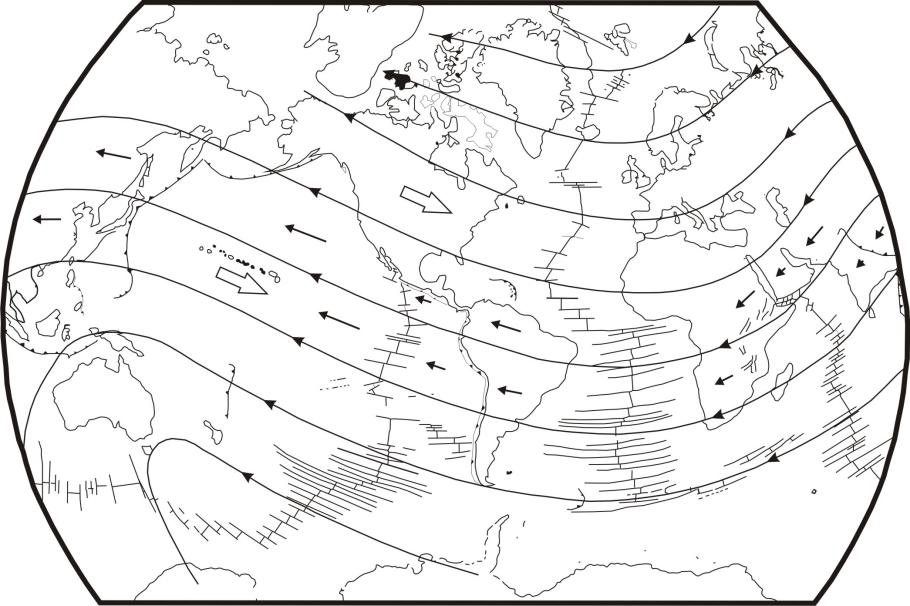
Doglioni，1990  大白箭头指示相对于向东的地幔流，小的黑箭头指示板块的西向运动

图4-5  推断的板块运动流线图^[2]44

从上面Doglioni的论述看，他仍认为大规模的大陆水平运动，是地球自转引起的。而事实是洋中脊的存在，被动大陆边缘和俯冲带的存在，以及前述应力值得计算，根本就支持不了这种大规模的大陆水平运动。另外，硅铝物如何来源？如何汇聚或者引用李三忠教授言硅铝物“板块如何登陆”？这个问题没有解决前谈大陆漂移在此认为为时过早。但根据前面均匀球体自转形成椭球体看，自转速度的改变，根据方程式（A1）球内合引力场将要发生改变。球内不同圈层的物质要发生运动，更何况地球自身还存在章动，以及球内物质的黏度的不同。根据球内性质，速度的改变，将建立新的平衡以满足球内物质稳定的需要，出现图4-5的流线形态也是自然的。

外核的黏度最低，软流圈次之，而地幔是高温下的固相，地壳是低温下的固相。在建立新的平衡过程中，根据F=mE(r)，黏度越低的球层反映，约束力较小，反映越迅速。外核的黏度比软流圈低，所以外核的迅速反映快速的作用到地幔；其次是软流圈，软流圈的的上作用到低温的壳层，下作用的地幔；而地幔在上下及自身的调整的作用下，通过也在调整的软流圈作用到地壳；它们这些作用力与也处在调整中的作用力共同作用到地壳。地球自转变化时，地球内部物质由赤道涌向两极或由两极涌向赤道。地壳由赤道向两极，同时在下部物质的作用下，在薄弱的地方引起有限距离的断裂或挤压现象，这是一，二是引起壳层的小幅度的垂直和水平运动。至于图4-5出现的方向性，大规模运移应是内部热运动等叠加到不断改变的自转上的综合表现。因此在此认为完全归功于地球自转，未免过于武断，但从上面的球内方程（A1），存在关联是一定的。

1992年Meyerhoff等，通过对全球许多构造的调查，列出了五十四种朝东定向的构造现象^[2]44页，这些朝东现象根据方程（A1），无论自转变快与变慢，软流圈物质改变最快最大的地方是赤道，由赤道向两极则逐渐变小，出现朝东定向的构造现象是在情理之中。

从王仁院士的应力值计算到滕吉文院士的论述，以及前述的球内方程（A1），地球自转对构造的作用应仅限于小的构造运动和结合其它一些运动形成大的宏观图4-5流线展布。即便是李四光先生，关于地质力学力，李四光强调四种力^[6]：离极力；地球自转速度变化引起的力（上下运动的力和东西向的力）；重力均衡的作用；太阳与月球引起的潮汐力。同时还强调^[2]123页：不能忽视地热场和放射场等其它场能量互相转化。由此可见自转虽在李四光先生优先考量之位，但对其它能量认为也有作用。这种作用后面还将提及。

上面的分析，依据球内合力强度方程（A1），结合王仁院士的计算，滕吉文院士的论述，Doglioni工作，以及李四光先生强调的四种力等，不难得出如下的结论：地球的自转对于构造形成有作用，但不能引起陆体的大规模的运动。对这一结论后面还将补充新的证据。

7.3、地球的潮汐、固体潮与月球、太阳的关系

地球绕太阳运动，月亮绕地球运动。月球是离地球最近的地外星体，月球质量为7.349×10²²kg，月球绕地球的轨道为椭圆形，绕地平均公转周期27.32天；平均月地距离384403km，近地点363300km，远地点405493km，其所对应的在地球位置引力强度分别为E_平=3.32×10^-5m/s²，E_近=3.71×10^-5m/s²，E_远=2.98×10^-5m/s²。图4-6为太阳系全景示意图，地球围绕太阳椭圆轨道运行，太阳质量1.9891×10³⁰kg；地球绕太阳周期365.256天；平均日地距离1.50×10⁸km，近日点距离1.471×10⁸km，远日点距离1.52×10⁸km，其所对应的在地球位置引力强度分别为E_平=5.93×10^-3m/s²，E_近=6.13×10^-3m/s²，E_远=5.73×10^-3m/s²。

当月球围绕地球旋转时，当太阳、月球、地球处于不同的相对位置，根据（A3）式地球内部的合力强度因三者的位置关系不断地周期性变化，因此等压力面、等位能面，等合力强度面在不停动态在改变。三者处于一条直线上，当月球处于太阳与地球中间，朝向太阳一面的地球合力强度减小，背对太阳一面的合力强度增加，使得等压力面、等位能面、等合力强度面被改变，为建立新的平衡，又因地球外壳的粘性远大于海水，海水向朝向太阳的一面涌入，因而朝向太阳的一面引起强潮汐，背向太阳的一面形成落潮；对于地球内部，由于软流圈的黏度同样小于外壳和地幔，运动速度较快，因此使得外壳出现固体潮。而月球处在其它位置，固体潮和潮汐将变得减弱，最弱的时候是月全食。另外，强潮汐天文条件与地震火山活动有很好的对应关系^[8、9]，这是因为对于处于临界状态的点或块，合力强度的改变，使得该点或块的地应力增强，所起的作用只不过是临门一脚，在此认为加强这种规律性的总结，对于防灾减灾是有义的。对于太阳、地球、月亮三者处于其它相对位置，潮汐、固体潮相对较若较弱。月球周期性绕地球运动，杨学祥等（2004年）认为使得太平洋、印度洋的海底引起跷跷板的运动，进而影响到天气^[7、8、9]。同时也为马宗晋院士揭示的微韵律提供一种基础理论上的解释；短韵律、中韵律后面结合热等做解释。 

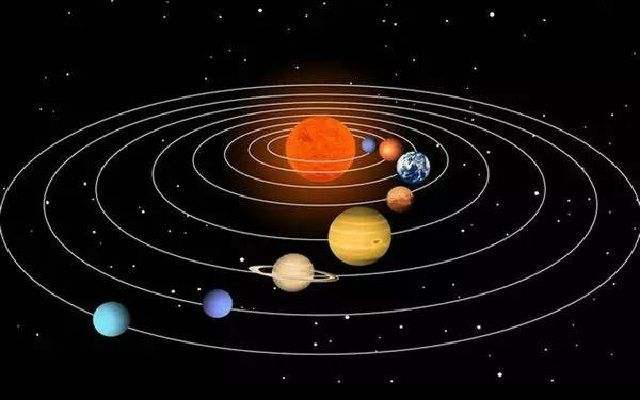
图4-6 太阳系全景示意图

潮汐和固体潮的产生，会引起物质的运动，这种运动的物质，会因物质黏度记录下来，就成了一种构造韵律构造。

7.4、构造运动的周期性问题的球内方程解释

表4-1列出了地球各圈层主要地质事件的旋回，表4-2列出了地球的韵律分级，图4-1地史上35Ma左右的重要地质事件集中期与穿越银道面时间对比。为什么会出现这样的周期性的规律，下面就依据据上面的球内方程讨论出现这些问题的缘由。

太阳系从图4-7中知道，它位于银河系银盘的猎户臂上，旋臂公转周期220～360Ma；银球直径2万光年，厚度1万光年；银盘厚度2000光年，银河系直径10万光年。银河系总质量4.1771×10⁴¹kg（目前有的认为银河系质量为5.9673×10⁴²kg），九成质量位于银盘上。太阳系距银心2.6万光年。太阳系绕银河系一周约2.5亿年，八次穿越银道面，周期约35Ma。根据图4-7，很难推出从太阳到银河系中心所有物质形成的引力强度在太阳处合引力强度公式，但可根据“一均匀球体或均匀球层在其外一点所产生的引力强度等于将其全部质量集中于球心所产生的引力强度”和高斯定理粗估其强度。根据高斯定理，2.6万光年以外的物质对太阳系的引力强度为零。2.6万光年以内物质保守估计不应少于银河系总质量的四分之一，即约10⁴¹kg（10⁴²kg）。因此可粗估引力强度为E_银=1.1×10^-4m/s²（或1.1×10^-3m/s²）。这一数据也不是一成不变的，它将随着猎户臂绕银心公转和穿越银道面而周期性变化。具体怎样变化目前还难以拿出具体算法，但并不妨碍对地球影响的分析。这一数据比月球对地球的引力强度大，但小于太阳对地球的引力强度，它同样可以影响引力潮和固体潮，进而影响地质记录。

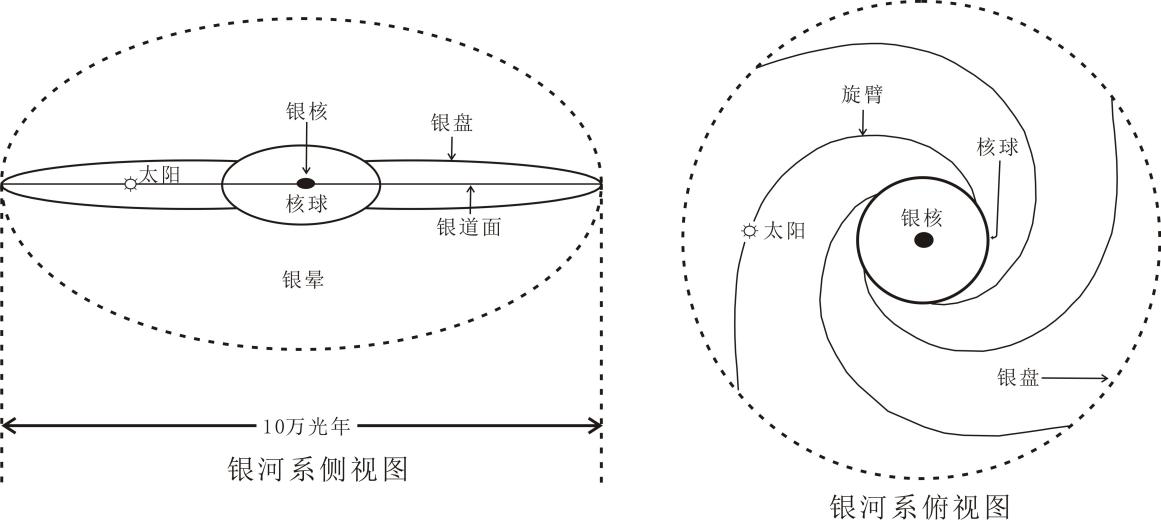
图4-7 银河系全景图和太阳系位于银河系的位置

表4-1地球各圈层主要地质事件的旋回，图4-1地史上35Ma左右的重要地质事件集中期与穿越银道面时间对比，以及表4-2地球的长韵律分级。关于长韵律的成因，有地外和地内起因论两种解释^[2]38。地外起因论认为，35Ma的韵律性，与太阳系穿越银道面一次的时间接近（见图4-1）；65Ma左右的周期是太阳系在银饼上、下做波动状运动的结果；100Ma左右的周期是由于太阳系围绕银河系中心运动过程中，处于远银心点和近银心点所受影响不同而引起的；220Ma左右的周期是受银河系周期自旋运动的影响。地内起因论认为，将联合古陆的分散归因于上升超地幔柱的作用，将联合古陆的形成归因于超地幔柱的影响，它们对应于D〞层以上的全地幔对流系统（Maruyama，1994；邓晋福等，1996）；将35Ma左右的韵律归因于地幔柱周期性脱离核-幔边界。

地外起因论和地内起因论，根据各自的论述显然都有道理，都应存在。然而二者的存在从上述球内方程（A3）看，又可得到统一。这是因为地球在绕银心和上下穿越银饼的周期性运动过程中，地球受到地球到银心一切星球的引力作用，这种作用前面用引力强度做了粗估，其引力强度量级介于月球和太阳之间。月球和太阳都能使地球产生潮汐、固体潮，相比之下粗估的周期性的引力强度造成地球内合力强度的改变，从而影响地球内物质的展布。而地球绕银心一周，八次穿越银到面间隔为35Ma左右。穿越银到面时有最大的地外引力强度作用于地球，过此则逐渐变小，因此地史上35Ma左右的重要地质事件集中发生是有道理的，因而地外起因论和地内起因论是一回事。陨击35Ma左右的发生，可以做如下的分析，太阳系到达银道面，使得太阳系的小星带中的，小行星原有的稳定轨道受到前述粗估的引力强度的制约，导致其中小行星撞向地球，使地球的局部质量增加。从而影响球内物质的展布，根据前述的球内性质，表4-1的除陨击外，其它除受粗估的引力强度的制约，还将叠加陨击带来的作用。多言一句的是，万天丰、尹延鸿二位地质学家曾著文^[1]讨论陨击是地球构造运动的动力，然根据球内方程的讨论，球内性质，以及共同定理，陨击难以引起大规模的明显水平或垂直的构造运动，但具有全球性作用是客观存在且肯定的。这仅是一家之言，如有不当请批评指导！

对于短韵律、中韵律在此可以这样理解。地外引力强度的周期，是多种多样的，这些周期与地球自身各种周期的叠加，根据“量的积累，会发生质的改变”这一客观规律，出现短韵律、中韵律事件应当是存在的。要找出这些周期，已超出时下的范围，故不再多言。

8、对球内合力强度方程应用总结

综上，通过求解球内合力强度方程，并应用这些方程，解释了各种韵律的形成，同时将地球自转作用回归理性，起到进一步助力。如有不当还请老师们批评指正！

参考文献

[1]万天丰 尹延鸿  全球岩石圈板块为什么会运移？[J]  自然杂志  2019第41期  

[2]巫建华 刘帅  大地构造学概论与中国大地构造学纲要[M]  地质出版社  2008年10月第一版

[3]李务伦  大地构造运动的动力系统架构及应用  山西科技  2019年第6期  37-44

[4]杨冬红 杨学祥 地球自转速度变化规律的研究和计算模型 地球物理学进展 2013年2月 28（1） 58-70

[5]滕吉文 宋鹏汉等  地球内部物质的运动与动力  科学通报  2016年  61（18）  1995-2019

[6]杨巍然 姜春发等 运用开合旋构造观探究地球内部是怎样运行的  地学前缘 2020年1月 27（1）

[7]杨冬红 杨学祥 地球自转速度变化规律的研究和计算模型 地球物理学进展 2013年2月 28（1） 58-70

[8]杨学祥  海底扩张的潮汐模式  大地测量与地球动力学  2003年5月  23（2）  77-80

[9]杨冬红  潮汐周期性及其在灾害预查中应用  吉林大学博士学位论文  2009年6月

[10]杨学祥等  地球差异旋转动力学  吉林大学出版社  1998年5月  30-31页

[11]傅承义 陈运泰 祁贵仲  地球物理学基础  科学出版社  1985年

[12]杨学祥等  地球内核快速旋转的发现及其动力学意义  地壳形变与地震  1998年2月

[13]杨学祥等 地球固体内核快速自转的理论证明和实测证实 西北地震学报 1996年12月 第18卷第四期

[14]杨学祥  陈殿友  地核的动力作用  地球物理学进展  1996年2月 第11卷 第一期