博文
《地球系统力学动力学》前四部分主干内容
|
由于笔者文字水平所限,已形成的《地球系统力学动力学》四篇文章,不方便阅读,下面将四篇文章的主要内容归纳简述于下。
第一部分 星球为球体的动力与球内稳定平衡基本性质
(一)、太空中可塑物质为球理论简述
单一可塑物质两分子存在引力与斥力,同时两分子质点间还存在万有引力。引力使得两分子相互靠近,斥力又使得两个分子相互依存存在有度,势能最小,并有新的质心出现,形成一个稳定系统。进一步的第三个分子进入,该分子与原两分子分别也存在上升关系,形成以各分子为顶点的等边三角形,且该分子质心与之前两分子的质心距离最短,新系统整体两势能最低。当第四个分子进入上述系统,依造上述原则形成以四分子质心为顶底的正四面体。而持续的同样分子的进入,在上述规则下,单一可塑物质就可以形成宏观上的球。这里面既有微观分子作用力的贡献,又有万有引力的宏观各向相同力的加持,因此太空中一切可塑物质只能且只能为球。而在这球中一切质点均处于稳定平衡状态,内部物质对外物质形成支撑,外部物质对内部物质形成压力,每一位置都处在最低势能状态。
(二)、球内性质Ⅰ
均匀物质的球内具有以下球内稳定平衡性质,简称球内性质Ⅰ:
性质1:球内任意点引力强度方向均指向球心,该点引力线为过球心的直线。
性质2:球内等引力强度面、等压力面、等引力位面均为球形。
性质3:球内同球面上:引力强度值、引力位值、压力值处处相等。
性质4:球内同球面上,任意点横向引力强度梯度、引力位梯度、压力梯度均为零;任意点纵向引力强度梯度、引力位梯度、压力梯度值相等。
性质5:球内引力线与各参数等值球面垂直。
性质6:球内任一点的各向应力值与该点的压力值相等。
对于存在球内性质Ⅰ的球,球内、外引力强度、引力位、内部压力及球内稳定平衡力、稳定平衡支持力具有以下表达式:
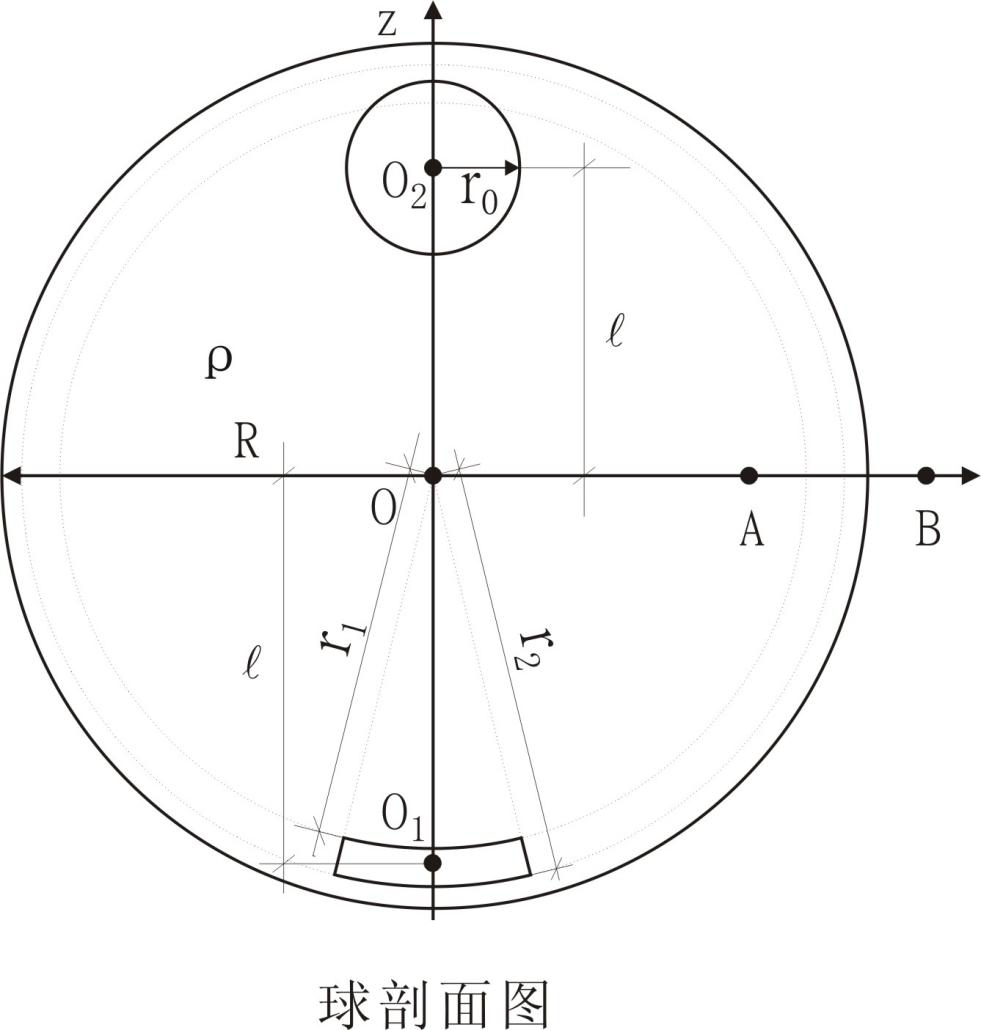
图1
(三)、引力强度计算公式
图1中B点引力强度: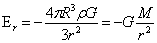 (r>R)…(1)
(r>R)…(1)
图1中A点引力强度: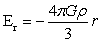 (r≤R)…(2)
(r≤R)…(2)
(四)、引力位计算公式
图1中O2为半径为r0的球为划定球剖面球心;O1为划定的旋转球台的剖面质心。
图1中B点引力位: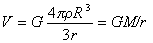 (r>R)…(3)
(r>R)…(3)
图1中A点引力位: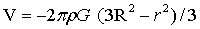 (r≤R)…(4)
(r≤R)…(4)
(五)、压力计算公式
图1中B点压力: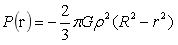 (r≤R)…(5)
(r≤R)…(5)
(六)、稳定平衡力、稳定平衡支持力计算公式
①图1中圆心O2球的稳定平衡力: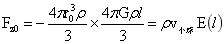 …(6)
…(6)
力的方向指向球心。
图1中圆心O2球的的稳定平衡支持力: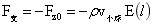 …(7)
…(7)
力的方向指向背离球心。
②图1中旋转球台的稳定平衡力:
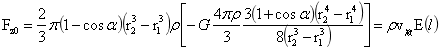 …(8)
…(8)
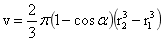 为旋转球台的体积,
为旋转球台的体积,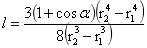 为均匀旋转球台的质心距O的距离,r1、r2为旋转球体内外半径,
为均匀旋转球台的质心距O的距离,r1、r2为旋转球体内外半径,
图1中旋转球台的稳定平衡支持力:
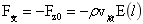 …(9)
…(9)
第二部分 上升力与下降力及浮力产生的数理根源
(一)、均匀球内异密度物质上升与下降成因引力场简述
①、异密度的物质的进入图2示的大球,图2中圆O1的圆即是,大球密度为ρ,小球密度为ρi(i=1、2),ρ1<ρ<ρ2。当小球的密度假设与大球相同,小球就多计或少计的质量为Δm=-ΔV(ρ-ρi)。这时的大球内的引力强度称为大球引力强度为式(2),小球多计或少计质量Δm的引起的引力强度--小球增量为:
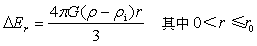 …(10)
…(10)
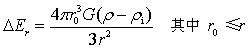 …(11)
…(11)
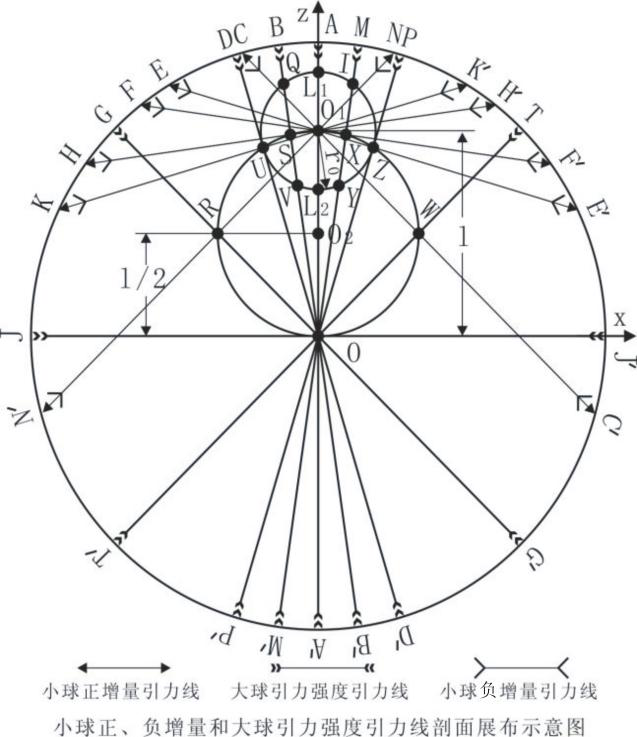
图2 球内引力线剖面展布示意图
式(10)、(11)中,i=1时小球增量--小球正增量方向背离小球球心;,i=2时小球增量--小球负增量方向指向小球球心。小球增量在图2示的经过大球球心的图示线段上投影有两个分量,一个平行该线段--小球平行增量,一个垂直该线段--小球垂直分量,这二分量展布规律分别见图3和图4。
由于小球增量分正负,所以小球平行增量、小球垂直分量也分正负。先看小球平行增量之小球平行正增量。小球平行正增量的展布大致特征见图3左侧图,在圆O2的圆上小球平行正增量为零,内部任意点小球平行正增量不为零且与大球平行正增量同向,外部的大球内则与之相反。在圆O2的圆内因小球小球平行正增量与大球引力强度同向,圆O2的内部压力较不存在小球增量时压力增大,外部则与之相反。小球底部因此获得来自下部的托举力,小球上部减少的压力又促成小球上升,这是一。二、小球垂直正增量的展布见图4左侧,可以发现在大球的上半球Z轴开始,两侧小球垂直正增量对称但方向相反,随着远离Z轴,小球垂直正增量由最初的夹角为180度,不断的变小,到下半球的Z轴变为相对。而在小球的图示的周边,圆O2的圆与圆O1的圆的交点小球垂直正增量最大,沿圆O1的圆向上下则不断减小,由此小球外部带来对小球的横向减压,这样一来也促成小球的上升。通过上面的简单分析,就可以知道小密度的小球为什么会上升的引力场原因。对于i=2时的小球的下降,仅是方向不同,不再赘述。
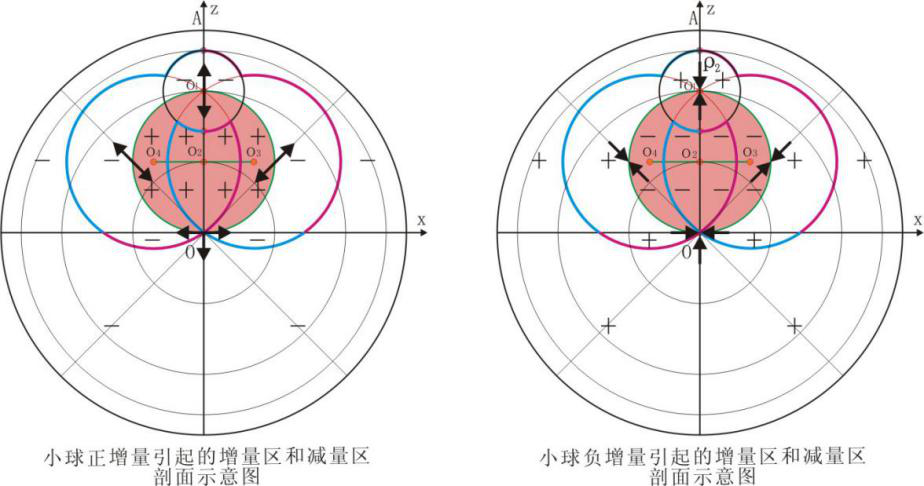
图3
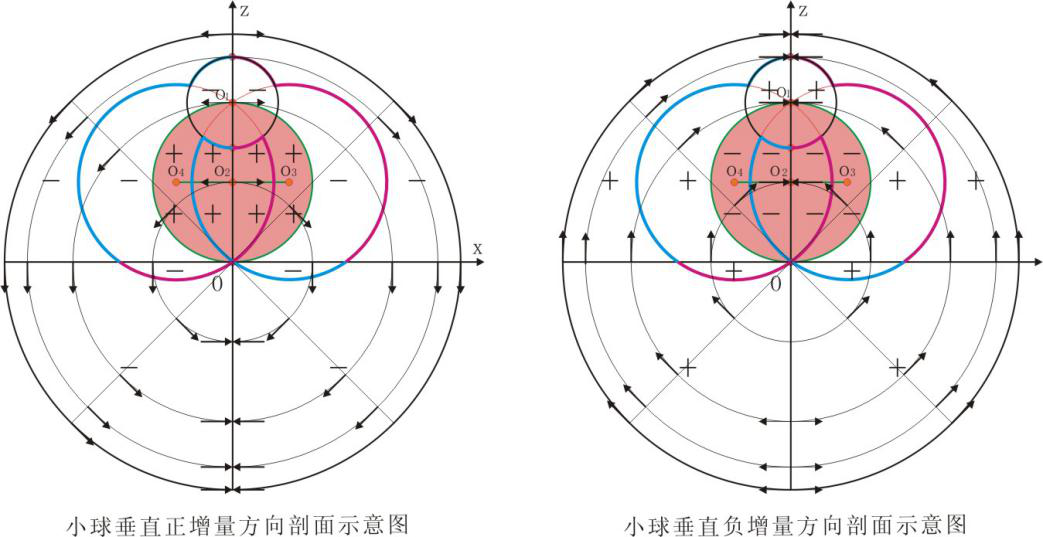
图4
②、上面用小球平行增量和小球垂直增量简析了小球的上升与下降,下面用另外的引力场分解办法分析小球的上升与下降。
大球引力强度可分解为:与z轴平行的大球引力强度分量(与xy平面垂直的分量)Ez和与平行xy平面的大球引力强度分量(与z轴垂直分量)Exy。而分量的式(2)的表达式为:
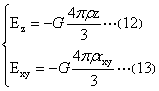
式(12)、(13)是大球内大球引力强度柱坐标系下的表达。
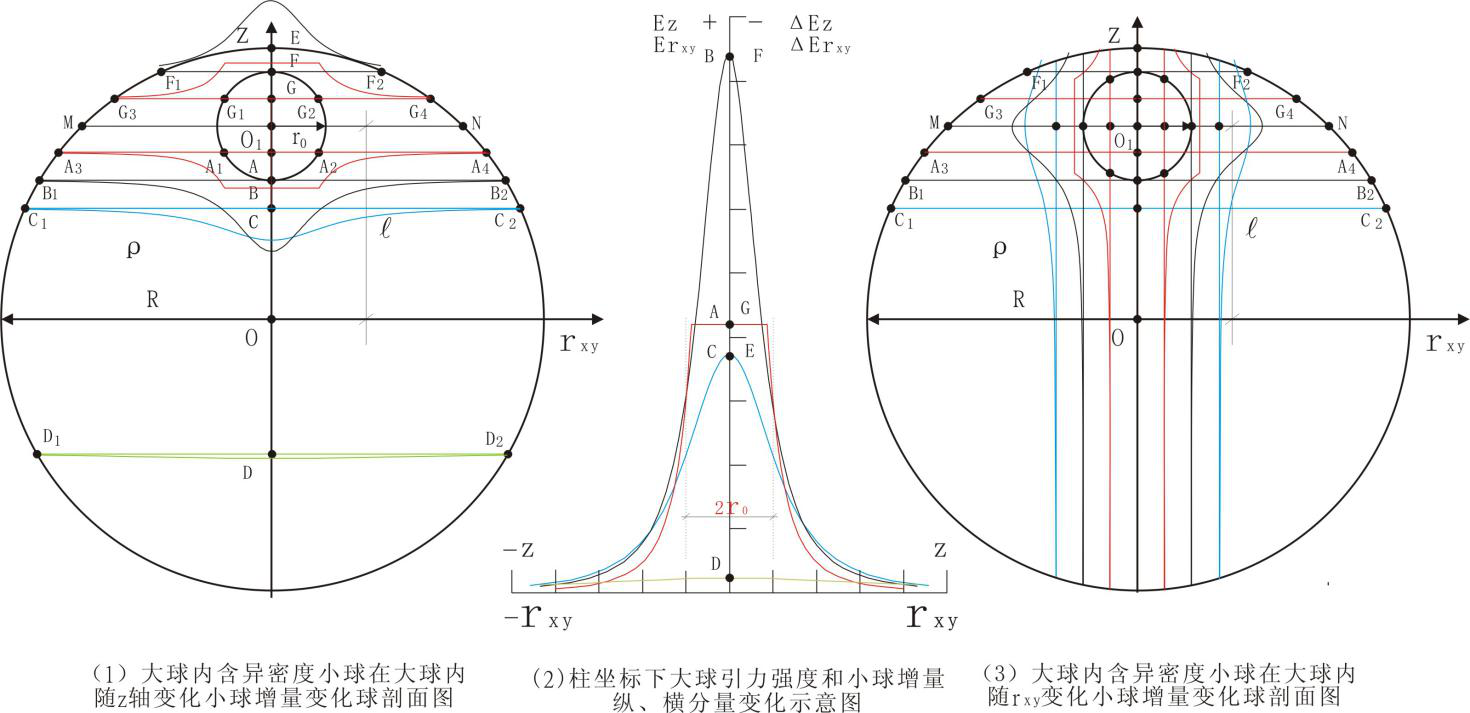
图5
对于小球增量式(10)、式(11)同样也分解为:与z轴平行的小球增量分量(与xy平面垂直的分量)ΔEz和与平行xy平面的小球增量分量(与z轴垂直分量)ΔExy。式(10)两分量表达式为:
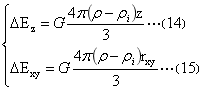
式(11)两分量表达式为:
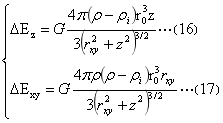
这四个方程是小球内外小球增量的柱坐标系下的表达式。当ρ>ρ1式(12)球内大球引力强度Ez在坐标系下,任意大球内平面方程z=z0上恒值,以平面方程z=0为对称,大球引力强度Ez方向都指向该平面;式(13)球内大球引力强度Exy在坐标系下,任意rxy=rxy0圆柱面上为定值,任意点方向平行xy平面,均指向z轴。二者变化见图5(2)红色曲线水平段,图5(1)、(3)红色曲线水平段和竖直段分别表示了大球引力强度Ez和大球引力强度Exy变化形态。
式(14)、(15)表示了图5中小球内部小球内部小球增量ΔEz和小球增量ΔExy,二者的变化与前述大球引力强度Ez和大球引力强度Exy相同。式(16)、式(17)表示小球外二者,纵横的变化形态,见图5图5(1)、(3)剖面图中黑色、蓝色等曲线。
从这图5(1)、(3)剖面两剖面中可以发现经小球圆心O1的xy平面,上部小球正增量ΔEz与大球引力强度Ez反向,在经小球圆心O1的xy平面和经圆心O的xy平面间小球正增量ΔEz与大球引力强度Ez同向,经圆心O的xy平面大球的下半球小球正增量ΔEz与大球引力强度Ez反向。这就使得原有的纵向的稳定与平衡被破坏,而破坏最严重的地方在小球的上下部位,以压力参数看,小球的顶部减压,底部增压。根据压力的特性,一增一减就形成了对小球的推动力。
小球正增量△Exy在在大球内rxy=rxy0每一圆柱面上的变化见图5(3),任意点的方向背离z轴,与Exy相反,这样一来就改变了原有大球圆柱上的平衡与稳定,改变最大的地方在图5(3)图示的小球周边。由于Exy与△Exy方向相反,使得小球水平的周边压力减小,为小球的上升提供方便及助力。通过以上简单分析就可得出小球密度小于大球密度时的上升;对于小球密度大于大球密度时也可通过同样的方法得出小球的下降,故不再赘述。
(二)、异密度小球在大球内的上升的动力学现象
上面分析出大球内异密度小球引起所有质点处于不平衡稳定状态,小球要么上升要么下降。在上升或下降过程中,大球内引力场也不断地改变。无论上升还是下降,快慢又受到物质黏度的影响,于是结合球内性质Ⅰ,大球内部以不同参数取舍可得到以下动力学:引力强度梯度动力学或重力动力学;引力位梯度动力学或势能动力学;压力或压力梯度动力学;质心动力学;拱形桥支撑力动力学;应力积累动力学或黏度动力学。由于以上动力学具有全球性,可总结出以下等时共同作用定理:栖于大球中的异于所栖位置大球密度的异密度物质,大球内所有质点间,不以物质的相态而存在不稳定的相互作用力,所有质点运动具有等时性。
(三)、上升力、下降力及浮力定力
上升力定理:栖于大球中的小密度物,小密度物多计质量受到不以物质的相态而存在的大球的排斥力,排斥力的大小为多计质量与大球在小密度物质心处大球引力场强度的乘积,即为:
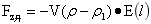 ,其中ρ>ρ1…(18)
,其中ρ>ρ1…(18)
下降力定理:栖于大球中的大密度小球,大密度物少计质量受到不以物质的相态而存在的大球的吸引力,吸引力的的大小为大密度物少计质量与大球在大密度物心处大球引力场强度的乘积,即为:
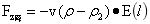 ,其中ρ<ρ2…(19)
,其中ρ<ρ2…(19)
浮力定理:栖于大球中的异密度小球受到大球不以物质的相态而存在,具有恢复小球所居位置再平衡大球的稳定平衡支撑力的作用,该力等于该异密度物排开大球物质受到的负引力,方向背向大球球心,数学表达式为:
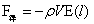 ,
,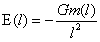 …(20)
…(20)
第三部分 球层的形成及含球层的球内性质
(一)、上一部分上升力、下降力及浮力的得出,为分异概念提供了数理根据内涵,也为球层的形成提供了数理根据,于是太空中多密度可塑物质可有以下球内性质,已命名为球内性质Ⅱ,内容如下:
性质1:球内任意点引力强度方向均指向球心,该点引力线为过球心的直线;
性质2:球内等引力强度面、等压力面、等引力位面均为球形;
性质3:球内同球面上:引力强度值、引力位值、压力值处处相等;
性质4:球内同球面上,沿球面任意点引力强度、引力位、压力梯度横向各参数梯度为零;纵向上任意点上,同半径的任意点各参数上梯度值相等。
性质5:球内引力线与各参数等值球面垂直;
性质6:球内任一点的各向应力值与该点的压力值相等。
性质7:所有物质,由球心而外,按密度从大到小圈层展布。
这些性质为地球具有球层成果提供了数理依据,是一切大的多密度物质星球为含球层球体稳定平衡提供了理论根据。
(二)、图6为有多密度物质形成的稳定平衡球层的剖面,满足球内性质Ⅱ,引力强度、上升力、下降力、浮力、引力位、压力计算表达式如下
①引力强度:图6球外一点B:
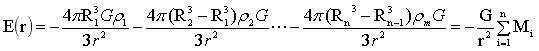 …(21)
…(21)
②图6球内Rm-1到Rm球层任意点A的引力强度:
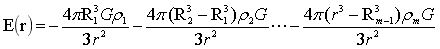 …(22)
…(22)
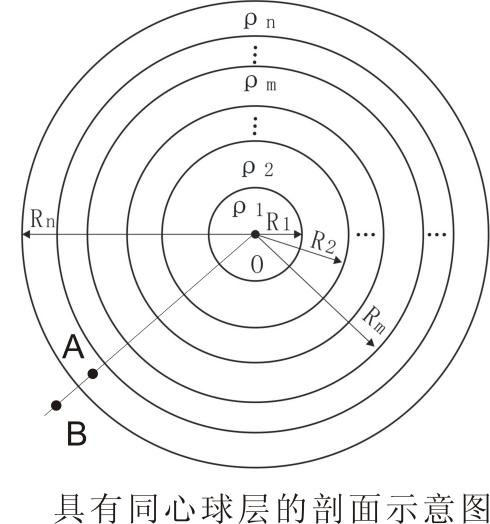
图6
③图6球内Rm-1到Rm球层若含异密度小球上升力、下降力及浮力:
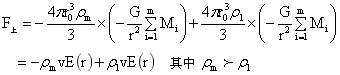 …(23)
…(23)
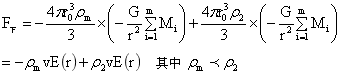 …(24)
…(24)
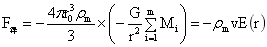 …(25)
…(25)
④压力
图6 Rn-1到Rn球层内任意点A的压力:
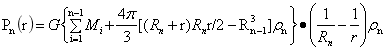 …(26)
…(26)
图6 Rn-1球面上的压力:
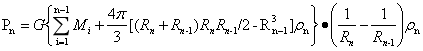 …(27)
…(27)
图6 Rm-1到Rm球层内任意点的压力:
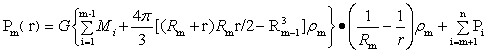 …(28)
…(28)
图6 内球球内任意点的压力:
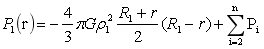 …(29)
…(29)
当Rn与地球半径一样大,从式(26)可推出由反复实验得出的静水压力公式Pn(r)≈-ρng(Rn-r)=-ρngh=pgh。
⑤引力位
图6点B的引力位:
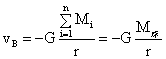 …(30)
…(30)
图6点A的引力位:
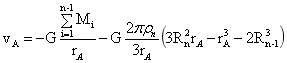 …(31)
…(31)
式(31)中当rA=Rn-1得:
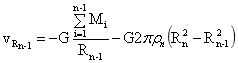 …(32)
…(32)
图6 Rm-1到Rm球层内如图中A点引力位:
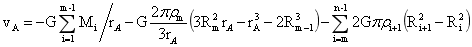 …(33)
…(33)
图6内球内如图中A点引力位:
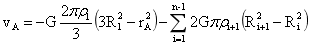 …(34)
…(34)
势能W=mgh这一反复实验得出的结论,可以根据式(30)、(31)推导出来,以式(30)为例,B点距球面距离为h时,球的半径与地球一般大小,h与地球半径相比可以忽略,引力位差:
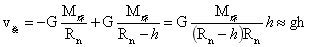 …(35)
…(35)
由于式(35)是单位质量做功差,质量为m的势能为W=mgh也就从理论上得出也就自然了。
(三)、平衡定理
图7 球心为O1、O2的两球密度ρ1相等且小于大球密度ρ。三球共切于A点,受力处于平衡,具有以下平衡方程:
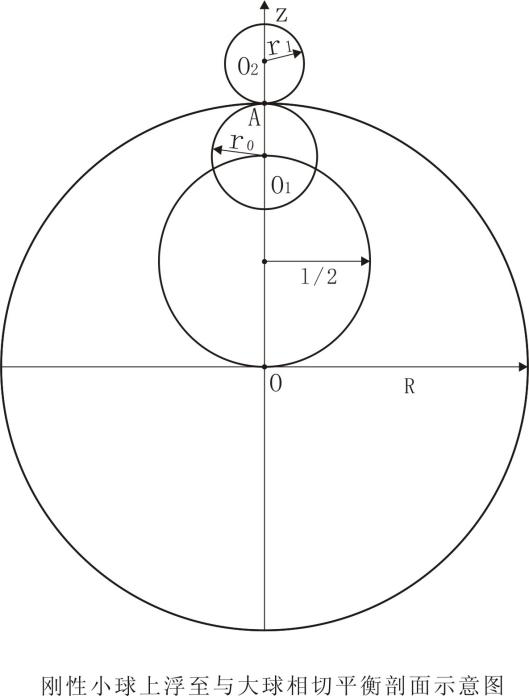
图7
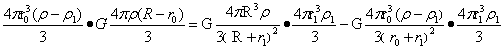 …(36)
…(36)
当R足够大是由此得出平衡定理:
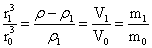 …(37)
…(37)
式(37)是普拉特和艾力计算补偿的理论根据,因此称为平衡定理。
(四)圈层化平衡作用定理
小球密度介于上下球层密度之间,且物质和黏度许可的情况下,小球物质最终将进行圈层化,将此称为圈层化平衡作用定理。
第四部分 球内合力强度方程及作用
(一)自转对球的影响
图8球内A点引力强度: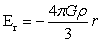 …(38)
…(38)
图8球内A点单位质量自转离心力: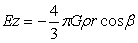 …(39)
…(39)
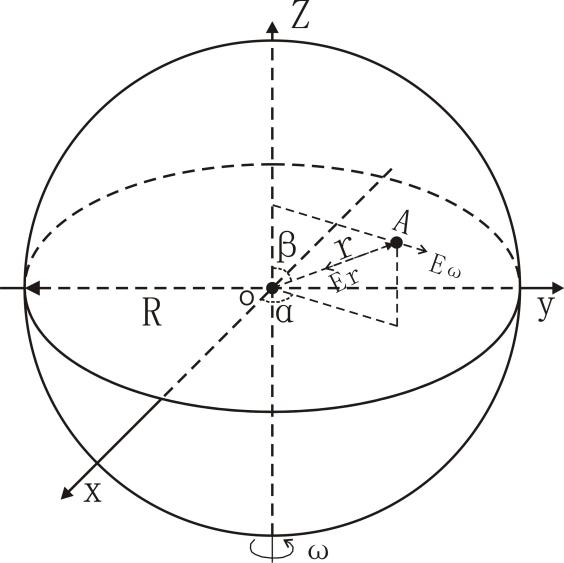
图8 旋转球体
式(38)、(39)A点的合力强度方程:
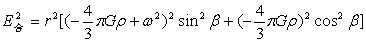 …(40)
…(40)
式(40)是椭球方程,也适用于含球层的球。可解释地球赤道两轴等长且长于旋转轴的形成,而赤道上的旋转强度Eω=0.03356m/s2。当旋转速度具有周期,根据杨学祥教授的研究各圈层存在差异性旋转,这对李四光院士提出的大陆阀动力机制有支持作用,但不支持大规模陆体的漂移。式(40)的向量方程为:
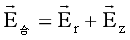 …(41)
…(41)
引力线方程:
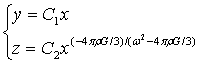 …(42)
…(42)
(二)外部引力场的影响
①月球对地球的影响
由于月球距地球较远,可以看作平行引力场,它在地球的引力强度约为E(y)=3.32×10-5m/s2。在式(41)上,加上月球在地球上引力强度向量,就可得如下椭球方程:
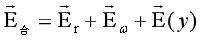 …(43)
…(43)
式(43)是一三轴不等的椭球方程。
②地外引力场对地球的影响
太阳距地球比月球更远,在地球处的引力强度约为E平=5.93×10-3m/s2,根据银河系的各种参数及太阳系在银河系的运动规律,根据高斯定理可粗估地球到银心的质量在地球处的引力强度为E银=1.1×10-4m/s2(或1.1×10-3m/s2)。这时的地外合一力场,可视为设地外引力场为:
![]() …(44)
…(44)
式中:t时间,r位于球内距球心距离,σ与Z轴夹角,τ在XY平面内与X轴夹角
对于图8的A点其合力强度为
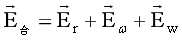 …(45)
…(45)
式(45)仍为椭球方程,但地外引力存在各种周期,如月球绕地球一周29天或三十天,地球绕太阳365.25天,太阳系围绕银心一周2.5亿年,八次穿越银道面。因此地球构造中,因物质有黏度特性,这些周期被记录,被观察到,如:潮汐现象、构造韵律等。
(三)球内性质Ⅲ
性质1:椭球球内任意点合力强度线为曲线,所有合力强度线止于球心,除椭球心外,任意点合力强度线切线偏离椭球球心。
性质2:椭球球内等合力强度面、等压力面、等合力位面均为椭球形。
性质3:椭球内同椭球面上:引力强度值、引力位值、压力值处处相等。
性质4:椭球内同椭球面上,沿椭球面任意点引力强度、引力位、压力梯度横向各参数梯度为零;纵向上任意点上,各参数上梯度值相等。
性质5:椭球内引力线的切线与等引力强度面、等压力面、等引力位面垂直。
性质6:椭球内任一点的各向应力值与该点的压力值相等;
性质7:所有物质,由球心而外,按密度从大到小圈层展布。
性质8:椭球内所有质点具有动态平衡和周期性变化的特点。
未尽问题
以上从最基本的理论为基础,梳理了物质的堆砌机制,还没有触及时下人们目前最为关心的海洋、大陆形成及大陆漂移,这是接下来的工作。
https://blog.sciencenet.cn/blog-3433895-1520648.html
上一篇:柱坐标系下物质的上升与下降形成的引力场再分析
下一篇:中国人一千年前发明了蒸汽机