博文

解析多尺度变换用于函数模型分割的举例演示

已有 105 次阅读 2025-12-21 14:43 |系统分类:科研笔记

演示程序AmstSplit123.sce如本文后图片1.所示。其中函数[Par1,A1]=AmstSplitx0(X0,W0,Cwtx,LMWR)的输入X0为被处理序列，是在均匀分布的频率（单位rad/s）点W0上的采样值，Cwtx是控制解析多尺度变换的结构变量。输入向量LMWR有4个元素依次指定：希望在分割时选用的最小相对尺度值、最大相对尺度值，在解析多尺度变换域内截取单元时的单侧宽度与周期宽度的比值，截选频域加权序列之和时的阈值比例因子。Par1是计算参数输出矩阵；A1是时间、地点、版本等信息，用于程序产生的图片或备存数据等作标记。

第13行至19行的语句，选择尺度带，检测单元的位置。当只选到单个尺度用于定位分割时，强行复制、重复利用一次这个尺度上的数据。第20行显示主极值线的位置点和对数线性系数。第21行，对选用的变换数据的所有行求和而得一个行向量，对相应的频域小波加权序列也求和。

第37行至53行的语句，实现分割和单元参数估计。在第38行，发现部分和序列长度已大于输入数据X0的点数的2倍时，抛弃其虚部，只留用其实部的2倍。在第44行，为了单元跨越周期化边界，延拓序列。在第47行，截取单元数据，搬移、补零。在第52行，把修正后的相位值换算到区间[-pi,+pi]上。

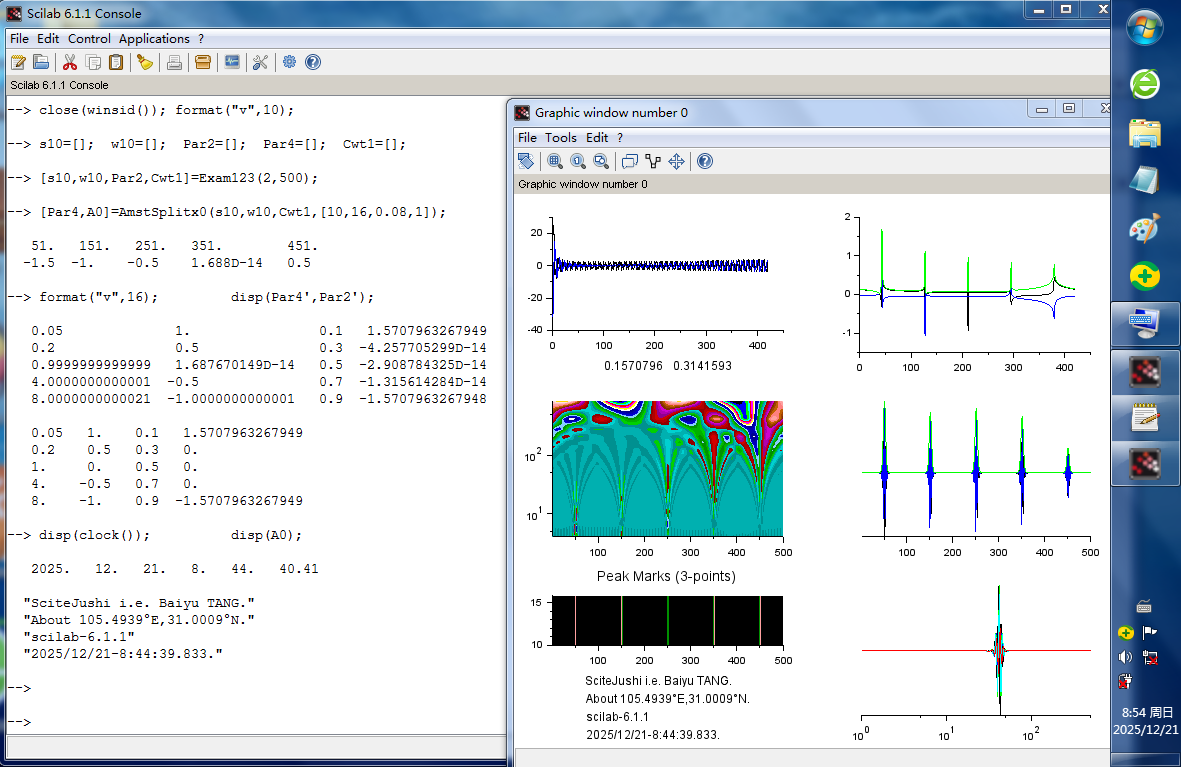
它的其余语句主要制图。例如本文后图片2.，在Scilab图形窗中的六个子图依次表示：输入的X0的实部、虚部曲线，对X0直接做离散傅里叶反变换所得序列的实部、虚部、模值曲线，解析多尺度变换（周期化的）输出矩阵的实部转置的图像，所选部分的和序列的实部、虚部、模值曲线，用3个数据点（不限像素）加宽标示的主极值点分布的图像，变换域统一开始点放置并补零加长后的单元序列的实部曲线（默认颜色设置，不管少数接近背景色难看清）。

程序中另一个函数[sx0,w1,Par3,Cwt]=Exam123(en0,FTL0)，设置变换控制参数Cwt，合成被处理数据序列sx0（在第75至79行）。sx0所在的频率点在序列w1中，Par3是单元参数的已知值矩阵。输入FTL0指定解析多尺度变换中DFT/IDFT（Scilab的FFT）的点数。输入en0可为3、2或其它，以抽选三个已知值矩阵中的一个；为3、2时，选用高斯函数的16阶导函数作基本小波，Cwt.WltLast=(1680)./(420:-2:1)，否则，选用高斯函数的2阶导函数作基本小波，Cwt.WltLast=(296.982)./(210:-0.2:1)。使尺度取值范围充分大，不仅包含分割所需的部分，而且可能察看影响锥混叠或高频截断数据所致的纹波。

自己写程序，难免随意改动，过些时侯，甚至对测试所用过的条件、过程等也可能记得不全准确。居士备存AmstSplit123.sce，以重测在今年博文中已呈现过的模型分割，都可用Scilab-6.1.1，组合调整对结果的影响可以被忽略。仍用2019年从亲戚那里来的一台lenovo笔记本电脑（2020-09-18《含噪频响数据的拟合以及Scilab辨识传函的局限》；位于东经105.4939度北纬31.0009度附近，上网用电脑USB口接手机号数据网，IP地址远在外地了这可能与手机号属地或网络运营商的业务联系有关）。

直接运行AmstSplit123.sce，相当于2025-03-17《解析多尺度变换用于函数模型分割和参数估计》中的精度较低测验，用了Exam123(1,1024)，第一、二采样点位于0.05、0.1Hz，LMWR=[3.5,7.5,0.04,1]。

然后，重复运行

close(winsid()); format("v",10);

s10=[]; w10=[]; Par2=[]; Par4=[]; Cwt1=[];

[s10,w10,Par2,Cwt1]=Exam123(3,1024);

[Par4,A0]=AmstSplitx0(s10,w10,Cwt1,[8,13,0.04,1]);

Er0=Par2; Er0(Par2==0)=1; Er0=abs((Par4-Par2)./Er0);

Er0(4,:)=abs(exp(%i*Par4(4,:))-exp(%i*Par2(4,:)));

disp(Er0',Par2'); disp(max(Er0(:)));

时，观察《在解析多尺度变换应用中的对偶域双重搬移数据的方法》（2025-06-13）中的测验，采样点分布中心在30GHz。

重复运行

close(winsid()); format("v",10);

s10=[]; w10=[]; Par2=[]; Par4=[]; Cwt1=[];

[s10,w10,Par2,Cwt1]=Exam123(2,1024);

[Par4,A0]=AmstSplitx0(s10,w10,Cwt1,[10,16,0.08,1]);

format("v",16); disp(Par4',Par2');

时，观察《解析窗对多尺度变换中极值线参数估计的影响》（2025-05-17）中的测验，第一、二采样点位于0.025、0.05Hz。

图片2.是运行

close(winsid()); format("v",10);

s10=[]; w10=[]; Par2=[]; Par4=[]; Cwt1=[];

[s10,w10,Par2,Cwt1]=Exam123(2,500);

[Par4,A0]=AmstSplitx0(s10,w10,Cwt1,[10,16,0.08,1]);

format("v",16); disp(Par4',Par2');

disp(clock()); disp(A0);

的情况。Par4与Exam123(2,1024)时相似。DFT和IDFT都隐含了周期化，其中数据点所在的实际自变量的符号随需要而变化。

遇到不含正频率成分的函数时，借助于自变量反号或函数值取复共轭运算，转化处理，不使用负的尺度值。如果解析多尺度变换（记入Tcwt）的结果s1的负频率分量全为零，那么s1的复共轭值的正频率分量全为零。

记得曾见到一个说法，雷达目标一个散射中心的小波变换有一条模极大值线；不知此说法的头尾和依据也没有方法，现也不能排除居士的这个记忆是虚假的。至少，实值小波函数，必有振荡波纹；数据截断窗，在对偶域有旁瓣。通常所谓的复值Shannon小波的模，明显不是单峰的；复值Morlet近似小波，在实用中高频也可能被截断。从《Wavelets An Analysis Tool》（M. Holschneider，1995年）一书早可了解其中的Progressive小波或函数及其模的特性。具体计算的极值线情况，靠实际观察。凭经验，本文的几个例子，利用解析多尺度变换的复数的模的主极值线，都成功地自动检测了单元数目和位置。

赛特（Scite）居士（Jushi）即唐（TANG）白玉（Baiyu）-2025-12-21。

图片1.解析多尺度变换用于函数模型分割的演示程序