分子间分子作用力与质点间质点作用力是可塑物质堆砌为球的源动力

李务伦

吉林省煤田地质局二零三勘探队

张学文老师曾让我探讨表面张力与太空中液体自动收缩为球的关系，因为手头资料较少，一时没有做答。近来收集到一些资料，读后就这一问题谈一点我的看法。通过研究发现分子间的分子作用力和质点间的引力的合力是可塑物质堆砌为球的源动力，也是一切星球为球的最底层逻辑。

1、所用到的基础物理理论

1.1、温度的统计意义简述

统计物理学指出：宏观量是相应的微观量的统计平均值^[6]9。如密度、压力、速度、能量等宏观量。经典物理范围内，温度的微观意义：温度是物质热运动强度的量度，是分子不规则运动平均平动动能的量度。每一平动自由度的平动动能：ε=kT/2(式中：ε一个平动自由度的动能，k玻尔兹曼常数，T绝对温度)。而一个平动自由度动能与相应平动速度的关系：ε=mV²/2(式中：为平动一自由度速度，m粒子质量)。也是一切星球为球最底层逻辑。

1.2、分子间作用力理论简述

分子的大小量级为10^-10m（10nm），一般都视为球形，这种球形有刚性和非刚性之分。科学的研究表明无论哪种球形，分子间的作用距离量级约10^-8m，作用力范围较短程。而分子间作用力又分斥力和引力，其经验公式分别为斥力公式f_斥(r)=λ/r^s(λ为常数)，引力公式f_引(r)=-μ/r^t(μ为常数)^[1]。引力将两个分子拉近，斥力又避免靠的太近，其本质是电子云相互交叠，使其存在状态可更稳定^[4]，见图1。分子的刚性球分子间力及作用势能见图2^[2]，非刚性球分子间力及作用势能见图3^[3]。

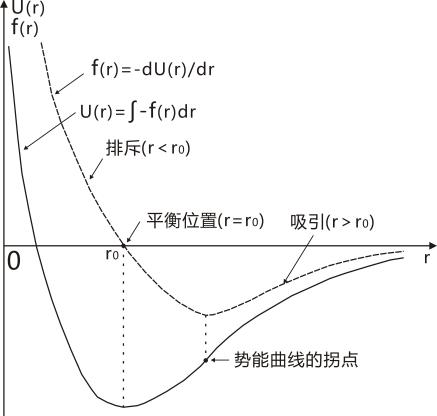
图1

结合上面关于分子间作用力的各种叙述，笔者认为图2示的刚性球模型、图1、3非刚性球模型，各表达了一类分子的分子间引力的具体情况，结合前述分子间作用力斥力和引力经验引力公式，分子间作用力斥力和引力一般情形可用下面的图4进行表述。

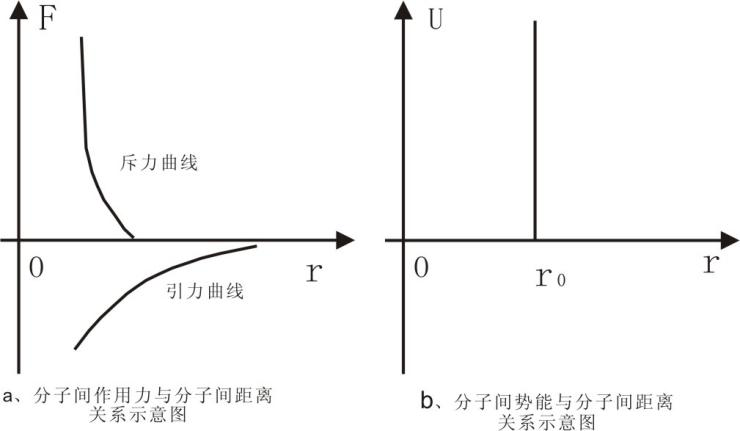
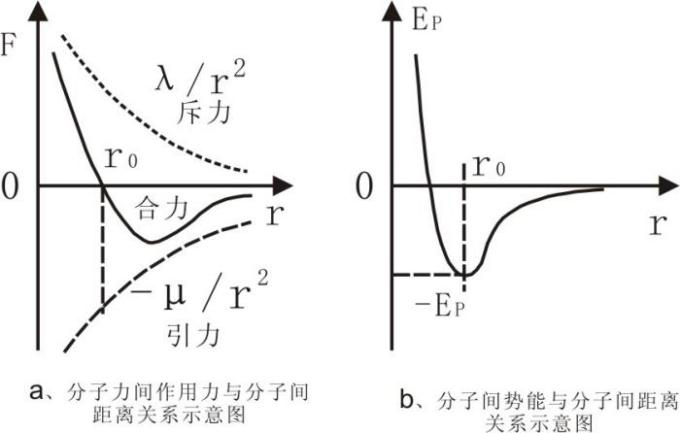
图2                                图3

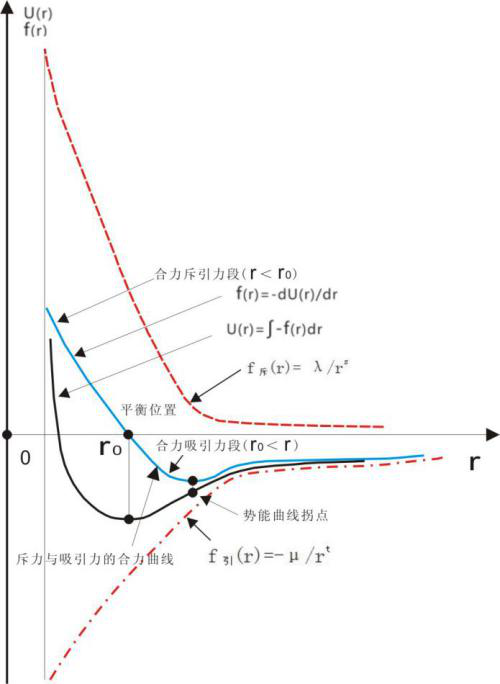
 图4  分子间作用力及势能综合示意图

上面归纳综合了已有能见到的文献各种分子间作用力的研究，这二作用力作用范围较小，至于如何产生这种作用力不做涉及，而是在这理论框架下，以分子为球，各向作用力相同，分子的质心位于球心，根据矢量线所满足的微分方程^[5]15：

dx/A_x=dy/A_y=dz/A_z…（1）

其分子作用力线方程如下：

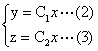
万有引力是质点与质点间的作用力，有万有引力定律F=-Gm₁m₂/r²定义的引力场强度如下：对于任意质量为m质点，质点在距离为r的一单位质点p所产生的引力场强度^[7]6（或简称引力场，即一单位质点在p点所受引力）E=-Gm/r²,r大于质点半径。万有引力作用力线和引力场引力线方程也为式（2）、（3）。

下面就应用上述理论讨论可塑物质的堆砌。在讨论这一问题前再图示叙述一下分子间作用力，见图5，在图中半径r₀为势能最小最小半径，至于具体的分子半径不做涉及。图5a表示了仅存在万有引力和分子间开始存在引力的状态，图5b表示了开始存在斥力的状态，图5c表示两分子在万有引力、分子间引力和在斥力的的作用下形成最稳定系统，质心在图示的切点上，此时两质点距离最小，而此时所占空间的表面积最小。

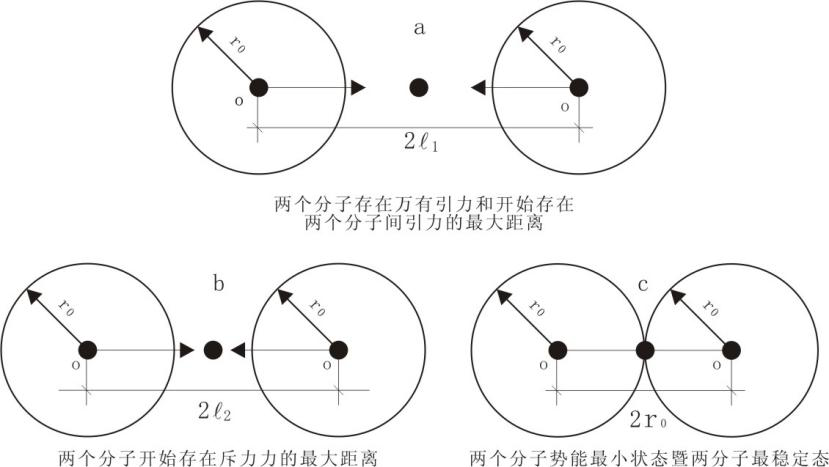
图5 两分子相互作用剖面示意图

2、多分子堆砌为稳定系统的推演

荷叶上经常可以见到滚圆的小水珠，类似这种小水珠还有水银珠等，它们是怎样形成的呢？下面应用上面理论尝试予以解答。

图5a表示了分子引力的最大作用范围；图5b表示了分子间斥力的最大作用范围；图5c中两个分子相互间处于最稳定状态-即势能处于最小状态，且体积是一分子的体积加一个直径和高度为分子直径的圆柱的棒状，质心位于棒状的中心（两分子的作用点上），该中心是新质点引力场的中心，2r₀是两分子质心的最短距离。

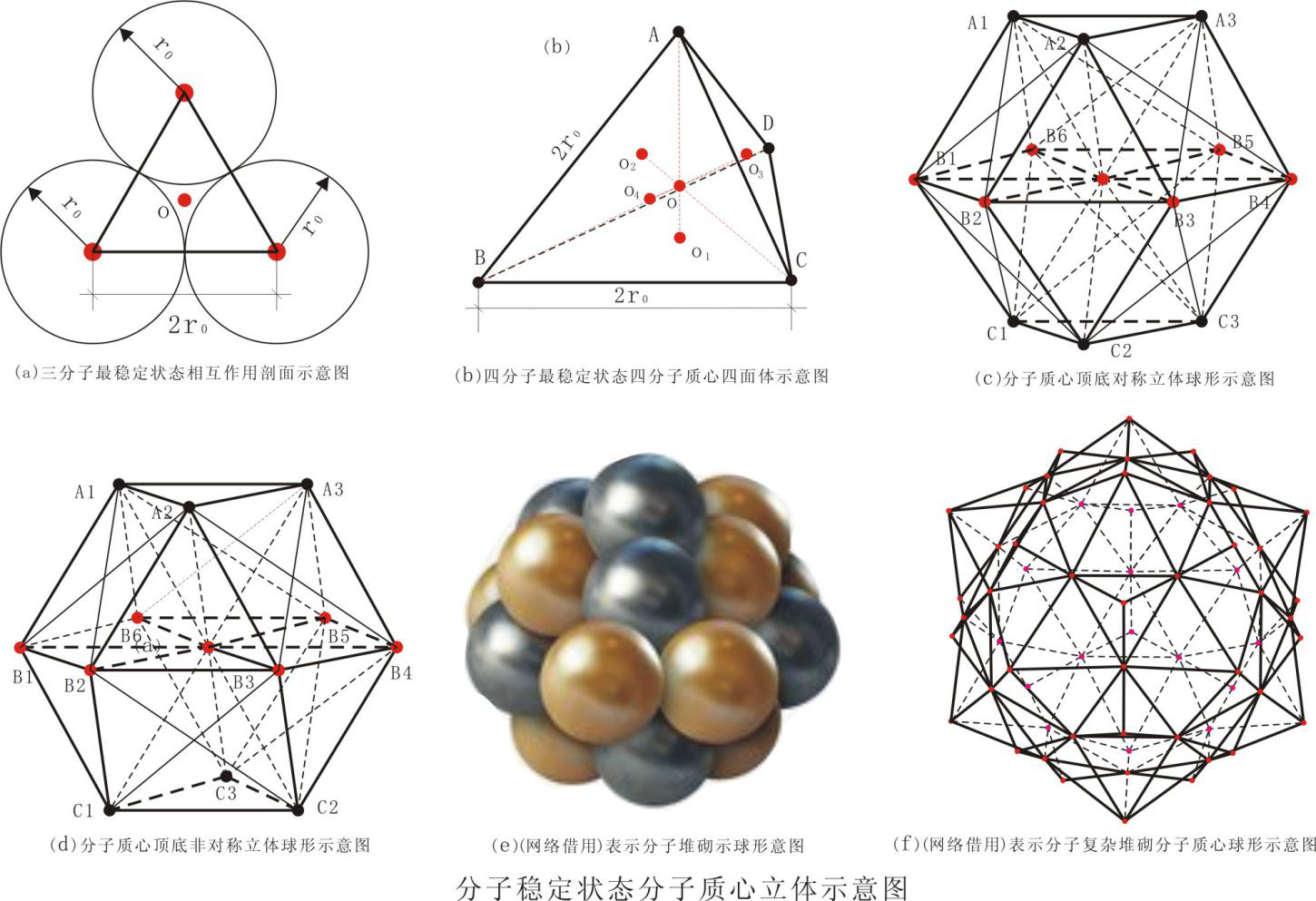
图6 分子相互作用示意图

而当第三个同样分子出现时，这个分子与图5c质点作用力方向在两个质心的连线上，当这个分子进入图5c所示的其中一个分子的作用力范围内时，必定是优先与这个分子形成稳定状态。但由于分子具有平动速度，处于不停的运动中，也处于新的引力场中，并不稳定，因此这一分子在分子间引力和新引力场的共同作用下，会与另一分子也结合为稳定状态。到此，三分子间的势能达到最小，新进入的的分子质心与图5c的质心距离最小。三个分子的质心位于等边三角形的顶点上，而形成三分子的最稳定平衡系统，见图6a，同时新引力场建立。此时的系统质心位于三分子质心形成的平面内，该质心与三分子的质心等距离。此时的体积是有三个棒状的部分与图6（a）三个分子球顶底相切的平面围限的区域。

当图6（a）稳定系统外部一个分子，首先在质点力的作用下，进入其中一个分子引力相互作用力范围内后，根据前面的理论和图6（a）三分子稳定结构形成可知：这个分子质心将与图6（a）中的三个分子的质心形成一个正四面体[见图6（b）]，以使所形成的系统势能最小，以使所形成的系统稳定，也遵守图6（a）质点与新加入分子质点作用力最短连线上。此时的体积是有六个棒状的部分与图6（b）三个分子球相切的四个平面围限的区域。O₁、O₂、O₃与图6（a）中O的意义相同，根据几何与物理知识知，此时所形成的系统质心位于图示的O点。O点到A、B、C、D距离相等，因此A、B、C、D四点在半径为AO的球面上，四个分子在半径AO+r₀球面内。

通过上面的讨论可得出以下推论：1、对于一个有多分子形成的稳定系统，任意新进入的分子，与之最近的三个分子质心等最短距离，各分子间势能最小；2、对于一个有多分子的稳定系统，任意新进入的分子，前者的质心与后者的质心距离最小。

根据上面的推论，对图6（b）这一稳定系统想象一下，当有更多的同样分子进入这一系统，在前面推论的规范下，会是怎样一番情况？首先是图6（b）四个面的三个分子，分别会接收一个同样的分子，形成稳定新稳定系统。这一稳定系统新进入的分子质心与前述的A、B、C、D一样共球面且同心。这个球的半径增加一个r₀后的球面后，新入的四个分子都内切于该球内。这时的稳定系统，图6（a）示的三分子质心平面共有十二个。这样以来会有更多的的同样分子，与上同样进入形成更新的稳定系统。反复重复这一过程将会得到图6（e或f）的具有球形的稳定堆砌。而包含所有这些分子的球面，以图6（b）O为球心。

以上系统叙述了一种分子在分子间作用力和质点间作用力，形成稳定堆砌球的可能过程，下面再叙述另一个可能的过程。以图6（b）的稳定系统为基础，十三个同样的分子首先形成图6（c或d）两个稳定堆砌十四面体结构。这两个稳定系统都以一个分子为中心，顶底各三个分子，中间七个分子在一个平面内。中心分子质心与其余十二个分子质心距离，均在分子间作用力和质点作用力合力下等长度。这两个稳定系统，完全符合遵守了前面的推论。这时的两个结构在半径为3r₀球面内，分子数达到最多，可划分得到图6（b）的稳定系统有八个和有十四个外平面。当图6（c或d）外部有更多的分子，将在前面推论规范下，重复前面分子堆砌，随分子的增多，堆砌成的稳定系统的球形半径逐渐增大，也会出现图6（e或f）的稳定系统。

当图6（e或f）稳定系统随分子的再增多，稳定系统半径将有纳米级到p级，再增多到毫米级，由于单个分子太小，人眼的分辨率所限，毫米级的分子稳定系统，以水为例，就可以看到滚圆的水珠。

3、稳定系统球与表面张力的关系

关于这种的类水珠状物的形成，过往使用表面张力来解释其形成。根据前面的叙述，显然不是妥当的。而关于表面张力的定义见到以下几种叙述：

1、关振民编《物理化学》上规定^[8]：在液体表面的边界上，表面张力垂直于边界线指向中心并于表面相切；对于弯曲表面，表面张力的方向与液面与切线垂直。2、刘志明等编《应用物理化学》上规定^[9]：若液体呈平液面，表面张力的作用点在平液面上，作用方向固定，总是垂直平液面；若液体呈弯液面，表面张力的作用点在凹或凸液面的切面上，作用方向总是垂直切面上。3、刘树德《如何理解表面张力》中规定^[10]：表面张力是跟液体表面共面或相切。4、鲁钟琪等表述为^[11]：表面张力就是液体表面层内分子相互吸引力不平衡的表现，它把液体表面层的分子紧紧拉向内部。但根据前面讨论看，表面张力定义为：“分子间的相互作用力和分子间质点作用力的合力的宏观表现”更为恰当。如果非要将分子间的相互作用力和分子间质点作用力的合力的宏观表现，描述为一种宏观力，也不是不可以，但在力的方向只能切于液体表面。这仅是我愚见，不当处还请老师们批评指导！

4、毛细现象的形成的再解释

毛细现象的形成用的解释是表面张力，这种解释根据前面的叙述，显然也不合理。下面提出我的看法，如有不当请老师们批评指正！先看图7，该图中展示了水和水银的毛细现象。

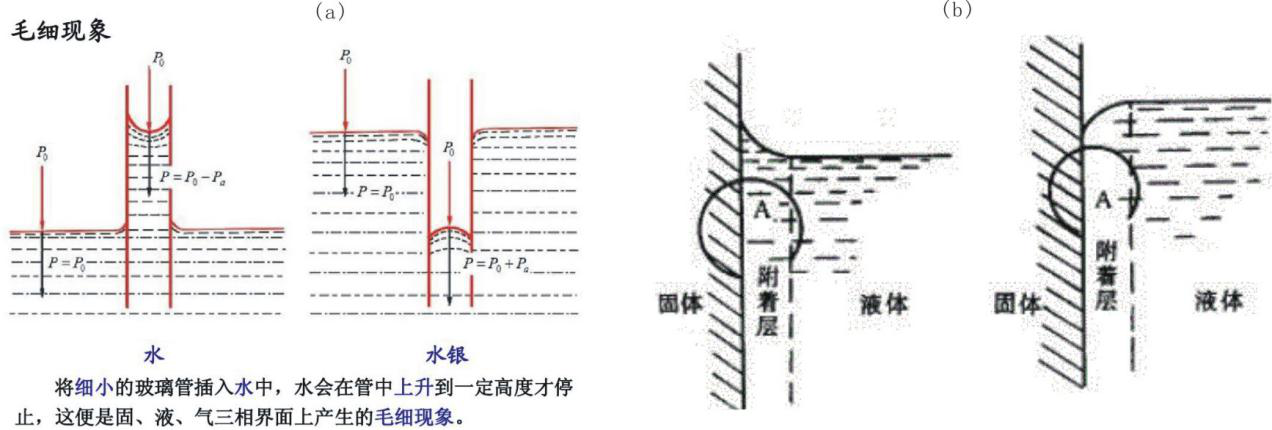
图7 来源于网络

图7中玻璃毛细管中的水柱高于水的液面，水银柱低于水银液面。出现这种情况的原因，根据前面的讨论，分子间作用力和分子质心间作用力看合力看，玻璃管的内表面分子与水分子的间也存在这种合力。自然水分子与水分子间也有这种合力，而这一且都处于地球的重力场中。玻璃分子与水分子间作用合力要大于水分子间的作用合力，不然水分子不会沿管壁爬升。水分子的沿管壁的上升，由于玻璃管较细，玻璃分子对水分子总合力，起初大于水柱的重力，因此将牵动相邻水分子的向上运动，待这种牵引力与水柱的重力相等，水柱将不再上升，同时在上升水柱的顶端存在一个抛物面。相反水银由于水银分子对玻璃分子的作用合力大，这对水银上升形成了阻碍，因此管内的水银高度要低于管外，且由于水银分子间的作用合力大，出现管内水银柱的上凸。

从上面的分析似乎可以得出：大密度的液体遇到小密度的固体，在毛细管中的高度低于外部，否者相反。用这一结论可以轻松解释，水遇到大密度的铁板时，水不再呈现球体，而是发生浸润。这些现象在图7中也有清晰的表达。

5、重力场对水珠等形态的影响

在荷叶上水珠较小时，水珠基本为正球体，但当水较多时，水珠呈偏的球体。出现这种现象的原因是，前者水分子间的作用合力力大于水珠在重力场中的受力，后者则与之相反，从而出现水珠变偏。

6、太空舱中可塑物质的状态及球内性质

太空舱远离地球表面，绕地球做圆周运动，处于引力场强度与圆周运动加速度合力强度基本为零状态。内部不规则的漂浮大量水，很快收缩为球。发生这一现象的原因，根据前面的推论可以方便的得以解答。在啰嗦一句，万有引力因是是长程力，使得相距较远的水相互靠近，并助力分子间力形成稳定系统，随稳定系统的增大助力作用越明显。

太空舱收缩为球的球内，由于分子间的分子力作用范围较小，所以也不影响球内如下已得出的性质；性质1：球内任意点引力强度方向均指向球心，该点引力线为过球心的直线；性质2：球内等引力强度面、等压力面、等引力位面均为球形。性质3：球内同球面上：引力强度值、引力位值、压力值处处相等。性质4：球内同球面上，任意点横向引力强度梯度、引力位梯度、压力梯度均为零；任意点纵向引力强度梯度、引力位梯度、压力梯度值相等。性质5：球内引力线与各参数等值球面垂直。性质6：球内任一点的各向应力值与该点的压力值相等。

6、结语

通过上面的讨论，无论是重力场中的各种小液体珠，还是太空舱中大量液体为球态，是分子间作用力和质点间作用力合力的共同结果。然而上述探讨是否正确还希望看到的老师提出批评与指导！对此首先表示不胜感激。也以此文向张学文老师交差，谢谢张老师的关心与指导！

参考文献

[1]范宏昌  热学[M]    科学出版社[M]  2003年2月

[2]騰维中  再论液体表面张力的微观机理  广西物理  2000年第2期

[3]姜兆华等  应用表面化学  哈尔滨工业大学出版社  2009年  P3-6

[4]黄淑清  热学教程[M]    高等教育出版社[M]  1985年6月

[5]谢树艺  矢量分析与场论  人民教育出版社  1978年12月

[6]王竹溪  统计物理学导论[M]    人民教育出版社[M]  1978年5月

[7]傅承义 陈运泰 祁贵仲  地球物理学基础  科学出版社  1985年

[8]关振民  《物理化学》  中国环境科学出版社  p359  2010

[9]刘志明 吴也平 金丽梅  《应用物理化学》  化学工业出版社  P124  2009

[10]刘树德  《如何理解表面张力》  中学物理  2010

[11]陆钟琪、郑洽馀  流体力学  机械工业出版社  1984

                                                                  2025年12月6日于哈尔滨