1999年的这篇文章，个人认为是涉及到近邻问题的研究领域，并且为核方法和降维方法提供很好的支持的很重要的文章。它的三个主要工作是：

1，说明并证明了数据集满足一定条件的前提下随着维度的增大，NN将变得毫无意义。

2，虽未给出证明，但从经验上给出了使得NN仍有意义的上限。

3，研究了满足不同概率条件的数据集，通过从IID（独立同分布）一步步将对数据集的概率分布的假设作松弛，分析了不同分布下的数据集是否存在上述问题。

    诸如KNN分类器，采用K-近邻图的谱聚类等许多算法，都涉及近邻图。而文章的工作说明，对于高维数据，不仅仅需要考虑到计算代价的问题，更要考虑到算法是否有效的问题。

    

    然而，NN并非在任何情况都是有意义的。下面的图说明，当query point到NN的距离，实际上和到许多其他点的距离很接近的时候，NN作用于算法中时效果并不好。这是直观上的描述。

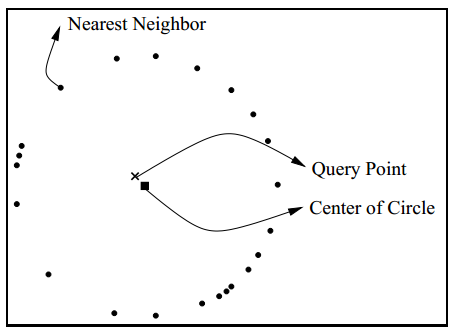
    上图中，数据集中的点呈一个圆形（二维的圆形或者是更高维的圆形），即存在一个圆心，到其中任何点的距离相同。此时如果query point距离圆心较近，虽然能够找到它的NN，但因为此点到其他点的距离和此点到NN的最短距离是相近的，NN于是变得意义不大。设想这是KNN算法中的情形，数据点是带有类标签的，当新样本点到两个类的距离都很接近时，它的类标签实际上会模糊不清。

   文章主要论述了下面的观点：

就是说，在数据集和查询点满足了前提条件（1）时，Q到任意点的距离都趋于相等！

定义1：如果一个随机向量的序列$A_1$,$A_2$,$\cdots$,$A_m$概率上收敛于一个常量，用极限的定义在形式上可表示为：

$\forall \varepsilon > 0,\mathop {\lim }\limits_{m \to \infty } P[\left\| {{A_m} - c} \right\| \le \varepsilon ] = 1$

则记为${A_m}{ \to _p}c$。

定理2（Slutsky's theorem）：如果${A_m}{ \to _p}c$且$g$是一个连续函数，则${g(A_m)}{ \to _p}g(c)$。

通过上面的定理证明命题1。

1

记${\mu _m} = E[{\left( {{d_m}({P_{m,i}},{Q_m})} \right)^p}]$，考虑随机变量序列$V_1$,$V_2$,$\cdots$,$V_m$，${V_{\rm{m}}} = {\left( {{d_m}({P_{m,1}},{Q_m})} \right)^p}/{\mu _m}$。则$E[V_m]=1$，且根据（1）得知，$\mathop {\lim }\limits_{m \to \infty } var({B_m}) = 0$，根据定理1，${V_m}{ \to _p}1$。

2

考虑随机变量${X_{\rm{m}}} = \left( {{{\left( {{d_m}({P_{m,1}},{Q_m})} \right)}^p}/{\mu _m},{{\left( {{d_m}({P_{m,2}},{Q_m})} \right)}^p}/{\mu _m} \cdots {{\left( {{d_m}({P_{m,n}},{Q_m})} \right)}^p}/{\mu _m}} \right)$，于是每个元素都服从和Vm相同的概率分布，既然${V_m}{ \to _p}1$，则${X_m}{ \to _p}(1,1,1,...,1)$。根据定理2，

${min(X_m)}{ \to _p}1$,${max(X_m)}{ \to _p}1$。

根据定理3，

$\frac{{\min ({X_m})}}{{\max ({X_m})}}{ \to _p}1$

而$DMIN_m=\mu _m min(X_m)$,$DMAX_m=\mu _m max(X_m)$,所以：

于是，

$\frac{{DMAX_m}}{{DMIN_m}}{ \to _p}1$

根据定义描述上式：

$\forall \varepsilon  > 0,\mathop {\lim }\limits_{m \to \infty } P[\frac{{DMA{X_m}}}{{DMI{N_m}}} - 1 \le \varepsilon ] = \mathop {\lim }\limits_{m \to \infty } P[DMA{X_m} \le (1 + \varepsilon )DMI{N_m}] = 1$

也就是说，前提条件（1）满足时，DMAX和DMIN趋于相等。注意以上证明并没有给m和p指定特别的意义。文章为m指定的意义是数据的维度（于是读者想到，如果为m指定诸如密度等其他意义，是否能得出类似结论？）。

1，如果数据在高维空间上能清晰地形成几个簇，那么NN是有意义的。就是说，如果查询点Q在某高维空间上的NN点，到Q的距离（DMIN）和其他点到Q的距离之间差值较大，那么NN还是有意义的。实际上这种情况下，前提条件（1）已经不满足了。

2，如果通过诸如PCA等降维方法，能有效地降维，那么NN也是有意义的。

第一种情况对应着核方法，而第二种情况对应着降维方法，这两种方法在聚类和分类等多个领域，都有广泛应用。