注册 |登录

xiaoqiugood的个人博客分享 http://blog.sciencenet.cn/u/xiaoqiugood

博文

自由电子的费米能级

已有 9904 次阅读 2013-11-22 03:32 |个人分类:电子结构计算|系统分类:科研笔记

关注：

1） 什么是 DOS for equivalent free-electron systems.

2) 什么样的金属是好的导体，什么样的是不好的导体，如何从费米能级附近的态密度看出来？


Density of states[edit]

The density of states (DOS) corresponds to electrons with a spherically-symmetric parabolic dispersion

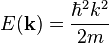E(.bold{k}) = .frac {.hbar^2 k^2}{2 m} ,

with two electrons (one of each spin) per each "quantum" of the phase space, 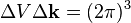.Delta V .Delta.bold{k}=(2.pi)^3 . In 3D, this corresponds to

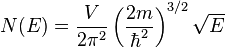N(E) = .frac {V}{2.pi^2} .left(.frac {2m}{.hbar^2}.right)^{3/2}.sqrt{E},

where 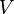V is the total volume.

Combining the expressions for the Fermi energy and the DOS, one can show that the following relationship holds at the Fermi level:

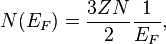
N(E_F) = .frac{3Z N}{2}.frac{1}{E_F},

where Z is the charge of each of the N metal ions in the crystal.





以下摘自：

http://www.eng.fsu.edu/~dommelen/quantum/style_a/cboxfe.html

 

6.10 Fermi En-ergy of the Free-Elec-tron Gas

        As the pre-vi-ous sec-tion dis-cussed, a sys-tem of non-in-ter-act-ing elec-trons, a free-elec-tron gas, oc-cu-pies a range of sin-gle-par-ti-cle en-er-gies.

       Now the elec-trons with the high-est sin-gle-par-ti-cle en-er-gies are par-tic-u-larly im-por-tant. The rea-son is that these elec-trons have empty sin-gle-par-ti-cle states avail-able at just very slightly higher en-ergy.

     There-fore, these elec-trons are eas-ily ex-cited to do use-ful things, like con-duct elec-tric-ity for ex-am-ple. In con-trast, elec-trons in en-ergy states of lower en-ergy do not have empty states within easy reach. There-fore lower en-ergy elec-tron are es-sen-tially stuck in their states; they do not usu-ally con-tribute to non-triv-ial elec-tronic ef-fects.

      Va-lence elec-trons in met-als be-have qual-i-ta-tively much like a free-elec-tron gas. For them too, the elec-trons in the high-est en-ergy sin-gle-par-ti-cle states are the crit-i-cal ones for the metal-lic prop-er-ties.

    There-fore, the high-est sin-gle-par-ti-cle en-ergy oc-cu-pied by elec-trons in the sys-tem ground state has been given a spe-cial name; the Fermi en-ergy. In the en-ergy spec-trum of the free-elec-tron gas to the right in fig-ure 6.11, the Fermi en-ergy is in-di-cated by a red tick mark on the axis.

     Also, the sur-face that the elec-trons of high-est en-ergy oc-cupy in wave num-ber space is called the Fermi sur-face. For the free-elec-tron gas the wave num-ber space was il-lus-trated to the left in fig-ure 6.11. The Fermi sur-face is out-lined in red in the fig-ure; it is the spher-i-cal out-side sur-face of the oc-cu-pied re-gion.


         One is-sue that is im-por-tant for un-der-stand-ing the prop-er-ties of sys-tems of elec-trons is the over-all mag-ni-tude of the Fermi en-ergy.

      Re-call first that for a sys-tem of bosons, in the ground state all bosons are in the sin-gle-par-ti-cle state of low-est en-ergy. That state cor-re-sponds to the point clos-est to the ori-gin in wave num-ber space. It has very lit-tle en-ergy, even in terms of atomic units of elec-tronic en-ergy. That was il-lus-trated nu-mer-i-cally in ta-ble 6.1. The low-est sin-gle-par-ti-cle en-ergy is, as-sum-ing that the box is cu-bic

.begin{displaymath} {.vphantom' E}^{.rm p}_{111} = 3.pi^2 .frac{.hbar^2}{2m_e} .frac{1}{{.cal V}^{2/3}} .end{displaymath}(6.15)


where $m_{.rm e}$ is the elec-tron mass and ${.cal V}$ the vol-ume of the box.

       Un-like for bosons, for elec-trons only two elec-trons can go into the low-est en-ergy state. Or in any other spa-tial state for that mat-ter. And since a macro-scopic sys-tem has a gi-gan-tic num-ber of elec-trons, it fol-lows that a gi-gan-tic num-ber of states must be oc-cu-pied in wave num-ber space. There-fore the states on the Fermi sur-face in fig-ure 6.11 are many or-ders of mag-ni-tude fur-ther away from the ori-gin than the state of low-est en-ergy.

      And since the en-ergy is pro-por-tional to the square dis-tance from the ori-gin, that means that the Fermi en-ergy is many or-ders of mag-ni-tude larger than the low-est sin-gle-par-ti-cle en-ergy ${.vphantom' E}^{.rm p}_{111}$.

      More pre-cisely, the Fermi en-ergy of a free-elec-tron gas can be ex-pressed in terms of the num-ber of elec-trons per unit vol-ume $I$$.raisebox{.5pt}{$/$}$${.cal V}$ as:

.begin{displaymath} .fbox{$.displaystyle {.vphantom' E}^{.rm p}_{.rm{F}} = .... ....hbar^2}{2m_e} .left(.frac{I}{{.cal V}}.right)^{2/3} $} % .end{displaymath}(6.16)


     To check this re-la-tion-ship, in-te-grate the den-sity of states (6.6) given in sec-tion 6.3 from zero to the Fermi en-ergy. That gives the to-tal num-ber of oc-cu-pied states, which equals the num-ber of elec-trons $I$. In-vert-ing the ex-pres-sion to give the Fermi en-ergy in terms of $I$ pro-duces the re-sult above.

It fol-lows that the Fermi en-ergy is larger than the low-est sin-gle-par-ti-cle en-ergy by the gi-gan-tic fac-tor


.begin{displaymath} .frac{I^{2/3}}{.left(3.pi^2.right)^{1/3}} .end{displaymath}



It is in-struc-tive to put some ball-park num-ber to the Fermi en-ergy. In par-tic-u-lar, take the va-lence elec-trons in a block of cop-per as a model.

     As-sum-ing one va-lence elec-tron per atom, the elec-tron den-sity $I$$.raisebox{.5pt}{$/$}$${.cal V}$ in the ex-pres-sion for the Fermi en-ergy equals the atom den-sity.

    That can be es-ti-mated to be 8.5 10$.POW9,{28}$ atoms/m$.POW9,{3}$ by di-vid-ing the mass den-sity, 9,000 kg/m$.POW9,{3}$, by the mo-lar mass, 63.5 kg/kmol, and then mul-ti-ply-ing that by Avo-gadro’s num-ber, 6.02 10$.POW9,{26}$ par-ti-cles/kmol.

    Plug-ging it in (6.16) then gives a Fermi en-ergy of 7 eV (elec-tron Volt). That is quite a lot of en-ergy, about half the 13.6 eV ion-iza-tion en-ergy of hy-dro-gen atoms.

     The Fermi en-ergy gives the max-i-mum en-ergy that an elec-tron can have. The av-er-age en-ergy that they have is com-pa-ra-ble but some-what smaller:

.begin{displaymath} {.vphantom' E}^{.rm p}_{.rm average} = {.textstyle.frac{3}{5}} {.vphantom' E}^{.rm p}_{.rm {F}} .end{displaymath}(6.17)


To ver-ify this ex-pres-sion, find the to-tal en-ergy $E$ $.vphantom0.raisebox{1.5pt}{$=$}$ $.int{.vphantom' E}^{.rm p}{.cal V}{.cal D}{.,.rm d}{.vphantom' E}^{.rm p}$ of the elec-trons us-ing (6.6) and di-vide by the num-ber of elec-trons $I$ $.vphantom0.raisebox{1.5pt}{$=$}$ $.int{.cal V}{.cal D}{.,.rm d}{.vphantom' E}^{.rm p}$. The in-te-gra-tion is again over the oc-cu-pied states, so from zero to the Fermi en-ergy.

      For cop-per, the ball-park av-er-age en-ergy is 4.2 eV. To put that in con-text, con-sider the equiv-a-lent tem-per-a-ture at which clas-si-cal par-ti-cles would need to be to have the same av-er-age ki-netic en-ergy. Mul-ti-ply-ing 4.2 eV by $e$$.raisebox{.5pt}{$/$}$$.frac32k_{.rm B}$ gives an equiv-a-lent tem-per-a-ture of 33,000 K. That is gi-gan-tic even com-pared to the melt-ing point of cop-per, 1,356 K. It is all due to the ex-clu-sion prin-ci-ple that pre-vents the elec-trons from drop-ping down into the al-ready filled states of lower en-ergy.



Key Points
$.begin{picture}(15,5.5)(0,-3) .put(2,0){.makebox(0,0){.scriptsize.bf0}} .put(12... ....thicklines .put(3,0){.line(1,0){12}}.put(11.5,-2){.line(1,0){3}} .end{picture}$The Fermi en-ergy is the high-est sin-gle-par-ti-cle en-ergy that a sys-tem of elec-trons at ab-solute zero tem-per-a-ture will oc-cupy.


$.begin{picture}(15,5.5)(0,-3) .put(2,0){.makebox(0,0){.scriptsize.bf0}} .put(12... ....thicklines .put(3,0){.line(1,0){12}}.put(11.5,-2){.line(1,0){3}} .end{picture}$It is nor-mally a very high en-ergy.


$.begin{picture}(15,5.5)(0,-3) .put(2,0){.makebox(0,0){.scriptsize.bf0}} .put(12... ....thicklines .put(3,0){.line(1,0){12}}.put(11.5,-2){.line(1,0){3}} .end{picture}$The Fermi sur-face is the sur-face that the elec-trons with the Fermi en-ergy oc-cupy in wave num-ber space.【只有金属才有费米面】


$.begin{picture}(15,5.5)(0,-3) .put(2,0){.makebox(0,0){.scriptsize.bf0}} .put(12... ....thicklines .put(3,0){.line(1,0){12}}.put(11.5,-2){.line(1,0){3}} .end{picture}$The av-er-age en-ergy per elec-tron for a free-elec-tron gas is 60% of the Fermi en-ergy.



6.9 Ground State of a Sys-tem of Elec-trons

       So far, only the physics of bosons has been dis-cussed. How-ever, by far the most im-por-tant par-ti-cles in physics are elec-trons, and elec-trons are fermi-ons. The elec-tronic struc-ture of mat-ter de-ter-mines al-most all en-gi-neer-ing physics: the strength of ma-te-ri-als, all chem-istry, elec-tri-cal con-duc-tion and much of heat con-duc-tion, power sys-tems, elec-tron-ics, etcetera. It might seem that nu-clear en-gi-neer-ing is an ex-cep-tion be-cause it pri-mar-ily deals with nu-clei. How-ever, nu-clei con-sist of pro-tons and neu-trons, and these are spin $.leavevmode.kern.03em .raise.7ex.hbox{.the.scriptfont0 1}.kern-.2em /.kern-.2em.lower.4ex.hbox{.the.scriptfont0 2}.kern.05em$ fermi-ons just like elec-trons. The analy-sis be-low ap-plies to them too.

     Non-in-ter-act-ing elec-trons in a box form what is called a free-elec-tron gas. The va-lence elec-trons in a block of metal are of-ten mod-eled as such a free-elec-tron gas. These elec-trons can move rel-a-tively freely through the block. As long as they do not try to get off the block, that is. Sure, a va-lence elec-tron ex-pe-ri-ences re-pul-sions from the sur-round-ing elec-trons, and at-trac-tions from the nu-clei. How-ever, in the in-te-rior of the block these forces come from all di-rec-tions and so they tend to av-er-age away.

      Of course, the elec-trons of a free elec-tron gas are con-fined. Since the term “non-in-ter-act-ing-elec-tron gas” would be cor-rect and un-der-stand-able, there were few pos-si-ble names left. So free-elec-tron gas it was.

        At ab-solute zero tem-per-a-ture, a sys-tem of fermi-ons will be in the ground state, just like a sys-tem of bosons. How-ever, the ground state of a macro-scopic sys-tem of elec-trons, or any other type of fermi-ons, is dra-mat-i-cally dif-fer-ent from that of a sys-tem of bosons.

      For a sys-tem of bosons, in the ground state all bosons crowd to-gether in the sin-gle-par-ti-cle state of low-est en-ergy. That was il-lus-trated in fig-ure 6.2. Not so for elec-trons. The Pauli ex-clu-sion prin-ci-ple al-lows only two elec-trons to go into the low-est en-ergy state; one with spin up and the other with spin down. A sys-tem of $I$ elec-trons needs at least $I$$.raisebox{.5pt}{$/$}$2 spa-tial states to oc-cupy. Since for a macro-scopic sys-tem $I$ is a some gi-gan-tic num-ber like 10$.POW9,{20}$, that means that a gi-gan-tic num-ber of states needs to be oc-cu-pied.



Fig-ure 6.11: Ground state of a sys-tem of non-in-ter-act-ing elec-trons, or other fermi-ons, in a box.
.begin{figure} .centering .setlength{.unitlength}{1pt} .begin{picture}(... ...35){.makebox(0,0)[r]{${.vphantom' E}^{.rm p}$}} .end{picture} .end{figure}


In the sys-tem ground state, the elec-trons crowd into the $I$$.raisebox{.5pt}{$/$}$2 spa-tial states of low-est en-ergy. Now the en-ergy of the spa-tial states in-creases with the dis-tance from the ori-gin in wave num-ber space. There-fore, the elec-trons oc-cupy the $I$$.raisebox{.5pt}{$/$}$2 states clos-est to the ori-gin in this space. That is shown to the left in fig-ure 6.11. Every red spa-tial state is oc-cu-pied by 2 elec-trons, while the black states are un-oc-cu-pied. The oc-cu-pied states form an oc-tant of a sphere. Of course, in a real macro-scopic sys-tem, there would be many more states than a fig-ure could show.

The spec-trum to the right in fig-ure 6.11 shows the oc-cu-pied en-ergy lev-els in red. The width of the spec-trum in-di-cates the den-sity of states, the num-ber of sin-gle-par-ti-cle states per unit en-ergy range.



Key Points
$.begin{picture}(15,5.5)(0,-3) .put(2,0){.makebox(0,0){.scriptsize.bf0}} .put(12... ....thicklines .put(3,0){.line(1,0){12}}.put(11.5,-2){.line(1,0){3}} .end{picture}$Non-in-ter-act-ing elec-trons in a box are called a free-elec-tron gas.


$.begin{picture}(15,5.5)(0,-3) .put(2,0){.makebox(0,0){.scriptsize.bf0}} .put(12... ....thicklines .put(3,0){.line(1,0){12}}.put(11.5,-2){.line(1,0){3}} .end{picture}$In the ground state, the $I$$.raisebox{.5pt}{$/$}$2 spa-tial states of low-est en-ergy are oc-cu-pied by two elec-trons each. The re-main-ing states are empty.


$.begin{picture}(15,5.5)(0,-3) .put(2,0){.makebox(0,0){.scriptsize.bf0}} .put(12... ....thicklines .put(3,0){.line(1,0){12}}.put(11.5,-2){.line(1,0){3}} .end{picture}$The ground state ap-plies at ab-solute zero tem-per-a-ture.




https://blog.sciencenet.cn/blog-567091-743685.html

上一篇：电声耦合常数：成功运行例子文件 example03
下一篇：Build-intuition之 电子结构与晶体结构
收藏 IP: 128.84.126.*| 热度|

0

该博文允许注册用户评论 请点击登录 评论 (2 个评论)

数据加载中...
扫一扫，分享此博文

全部作者的其他最新博文

全部精选博文导读

相关博文

Archiver|手机版|科学网 ( 京ICP备07017567号-12 )

GMT+8, 2024-11-24 08:26

Powered by ScienceNet.cn

Copyright © 2007- 中国科学报社

返回顶部