博文
《走近混沌》-27-初级细胞自动机
 精选
精选
|||
第二十七章﹕初级细胞自动机
西方有句谚语:“在木匠眼里,月亮也是木头做的。”
古希腊哲学家泰勒斯说:万物之本是水。他的学生毕达哥拉斯说:万物之本是数。再后来又有赫拉克利特说:万物之本是火。中国哲学家孟子以心为万物之本。近代的哲学家有了物理知识,则说:万物之本是原子、电子等基本粒子。看来,哲学家们和木匠异曲同工,都希望把复杂的世界追根朔源到某一种简单的、自己理解了的东西。
如今这个计算机时代,有人宣称说:万物之本是计算。
这个人就是上世纪80年代后期开发著名的《数学》Mathematica符号运算软件的美国计算机科学家,史蒂芬·沃尔弗拉姆(Stephen Wolfram)。
实际上,沃尔弗拉姆并不是提出“万物之本是计算”的第一人。MIT计算机实验室前主任弗雷德金,早在上世纪80年代初就提出:“终极的实在不是粒子或力,而是根据计算规则变化的数据比特。”著名物理学家费曼在1981的一篇论文里也表达过类似的观点。
不过,沃尔夫勒姆沿着这条路走得更远。从古至今困扰人们的三个基本哲学问题:生命是什么?意识是什么?宇宙如何运转?按照沃尔夫勒姆在他的砖头级巨著“新科学”里的“计算等价原理”,生命、意识都从计算产生,宇宙就是一台‘细胞自动机’。
被人们称为天才的沃尔弗拉姆一九五九年生于伦敦,十五岁发表他的第一篇科学论文,二十岁获得美国加州理工学院的物理博士学位。之后,又荣获麦克阿瑟基金会的“天才”奖。当时,他将此奖项所获得的十二万五千美元的奖金全部用于了他感兴趣的基本粒子物理及宇宙学等方面的研究。
八十年代初期,即将离开加州理工学院,前往普林斯顿高等研究院进行研究的沃尔弗拉姆在一次研讨会上,初识了“细胞自动机”的理论,颇有一见钟情、相见恨晚的样子,一头扎进细胞自动机的研究之中。
沃尔弗拉姆在八十年代后期,因为开发了著名的《数学》符号运算软件而声名大振,且获得了商业上的成功。进入九十年代后,他便躲进小楼成一统,继续他所痴迷的细胞自动机工作,潜心著作一部“曠世之作”。直到2002年,沃尔弗拉姆奋战10年,经过无数次的敲键盘、移鼠标,终于产生出作者狂妄地自我宣称是“与牛顿发现的万有引力相媲美的科学金字塔”的巨著,名为:《一种新科学》。
在这部1200页的重量级著作中,沃尔弗拉姆将他所偏爱的一维自动细胞机中的“规则 110”的精神光大发扬,贯穿始终。根据书中的观点,各种各样的复杂自然现象,从弹子球、纸牌游戏到湍流现象;从树叶、贝壳、等生物图案的形成,到股票的涨落,实际上都受某种运算法则的支配,都可等价于“规则 110” 的细胞自动机。沃尔弗拉姆认为“如果让计算机反复地计算极其简单的运算法则,那么就可以使之发展成为异常复杂的模型,并可以解释自然界中的所有现象”,沃尔弗拉姆甚至更进一步地认为宇宙就是一个庞大的细胞自动机,而“支配宇宙的原理无非就是区区几行程序代码”。
《一种新科学》的出版在当时引起轰动,初版五万册在一星期之内销售一空,但是,学术界大多数专家们对此书的评价却不高。对沃尔弗拉姆傲慢自大、忽视前人的工作、自比牛顿的做法,更是嗤之以鼻,认为这是使用商业手段,对不熟悉细胞自动机的广大读者的一种误导。事实上,沃尔弗拉姆并未创立什么“新科学”,由冯·诺依曼提出的细胞自动机的理论,已有五十多年的历史,这个理论,以及基于复杂源于简单的道理的‘复杂性科学’,一直都是科学界的研究课题。
沃尔弗拉姆虽然言过其实,但他对细胞自动机的钟爱,对科学的执着,仍然令人佩服。况且,沃尔弗拉姆也不仅仅是空口说白话,而是用计算机进行了大量的论证和研究。比如,他认定了宇宙是个庞大的细胞自动机,但是有很多种不同的细胞自动机啊,宇宙到底是根据哪种细胞自动机运转的呢?我们在上一章中介绍过的康维的生命游戏,只是众多二维细胞自动机中的一种,如果变换生存定律,可以创造出一大堆不同的生命游戏来。此外,除了二维的细胞自动机,还可以有一维、三维、甚至更多维的细胞自动机。那么,宇宙遵循的是哪一种呢?
沃尔弗拉姆想,首先应该从最简单的一维细胞自动机开始研究。
像生命游戏那种二维细胞自动机,是将平面分成一个一个的格子。因此,一维细胞自动机就应该是将一维直线分成一截一截的线段。不过,为了表示得更为直观一些,我们用一条无限长的格点带来表示某个时刻的一维细胞空间,如图(27.1a)所示。用格子的白色或黑色来表示每个细胞的生死两种状态。并且,只考虑最相邻的两个细胞,也就是与其相接的“左”、“右”两个邻居的影响。如此所构成的最简单的细胞自动机被称为初级细胞自动机。
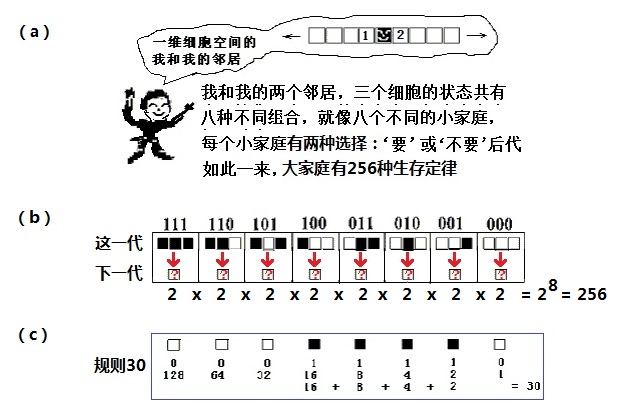
图(27.1):初级细胞自动机有256种
到底有多少种初级细胞自动机呢?一个细胞加上它的左右两个邻居,这三个细胞的生死状态(输入),决定了该细胞下一代(输出)的状态。因为三个细胞的状态共有八种不同的组合,因此,如图(27.1b)所描述的,初级细胞自动机的输入有八种可能性。对每一种可能的输入,下一代的中间那个细胞都有‘生’或‘死’两种状态可选择。所以,总共可以组合成28=256种不同的生存定律。也就是说,有256种不同的初级细胞自动机。
和我们介绍生命游戏一样,图(27.1b)中用二进制的0(空格)代表‘死’,1(黑色格子)代表‘生’。首先,将输入可能的八种情况按照111、110、101、100、011、010、001、000的顺序从左至右排列起来,然后,八种输入所规定的输出状态形成一个八位的二进制数。将此二进制数转换成十进制,这个小于256的正整数便可用作初级细胞自动机的编码。例如,图(27.1c)所示的输出状态可以用二进制数00011110表示,将其转换成十进制数之后,得到24+23+22+21 = 30。我们便把这个生存定律代表的初级细胞自动机,称为‘规则30’。
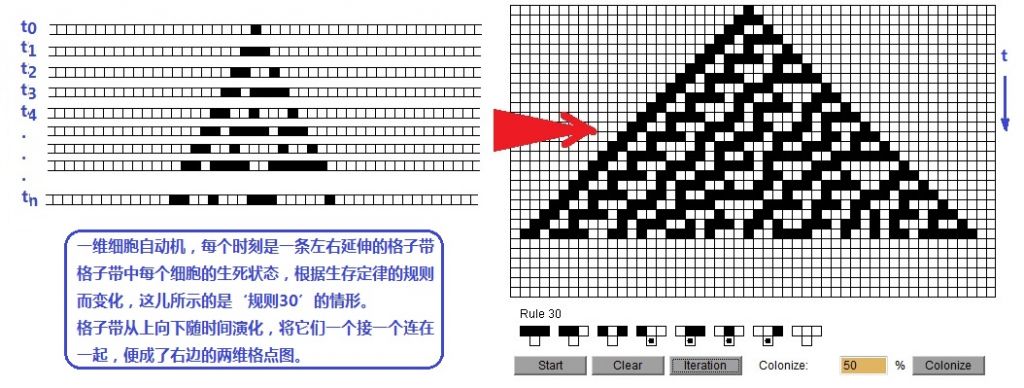
图(27.2):初级细胞自动机‘规则30’的时间演化图
初始时刻只有中间一个细胞为‘生’
Java program
http://mokslasplius.lt/rizikos-fizika/en/wolframs-elementary-automatons
为了显示一维细胞自动机中,细胞状态不同瞬时的演化情况,我们将每一个相继时刻对应的的格点带附在上一时刻对应的的格点带下面。如图(27.2)所示,在t0时刻的格点带,是一条只有中间一个格点为‘黑’,其余格点均为‘白’的左右延伸的长带子。图中,垂直向下的方向表示时间的流逝。因为加了一个时间轴,所以,虽然是一维细胞自动机,而计算机屏幕显示出来的却是一个二维格点图。图(27.2)显示了规则30的演化,图(27.3)给出了更多其它规则的初级细胞自动机的演化图形。
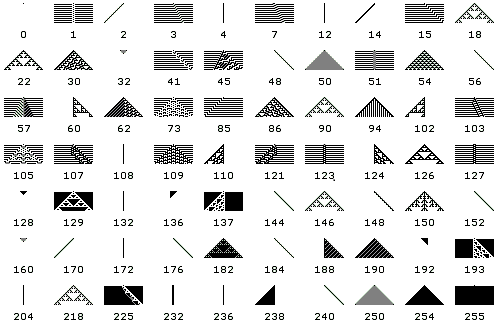
图(27.3):初级细胞自动机的时间演化图
图像来自Wolfram:
http://mathworld.wolfram.com/ElementaryCellularAutomaton.html
在沃尔弗拉姆发表的一系列论文中,对一维细胞自动机的代数、几何、统计性质作了系统深入的研究和分类。他还特别对其中初级细胞自动机的“规则 30”和“规则 110”的有趣性质情有独钟。图(27.4)给出这两种规则对于随机初始值的时间演化图。“规则 30”之所以特别是因为它的“混沌”行为,例如我们可以考查中心细胞的状态随时间演化所得到的二进制序列:1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, ...,可以证明,这是一个无穷不循环的伪随机序列。“规则 110”则更为有趣:在随机的初始条件下,却产生出好些看起来在一定程度上“有序”、但是又永不重复的图案。“规则 110”似乎揭示了无序中的有序,混沌之中包含着的丰富的内部结构,隐藏着更深层次的规律。沃尔弗拉姆的一个年轻助手库克后来(1994年)证明,“规则 110”是等效于通用图灵机的。

图(27.4):规则30和规则110
如何理解一个初级细胞自动机“等效于通用图灵机”呢?从生物学的角度看,细胞自动机的每一次迭代变化表现为细胞的生生死死,而从计算机科学的角度,每次演化却可看作是完成了一次‘计算’。
查查计算机的历史,曾经使用过一条长长的穿孔纸带作为输入输出,这听起来和我们这儿每个离散时刻的格子带有些类似。格点带上细胞的黑白生死分布,就对应于计算机纸带上的(0/1)“符号串”。可以想象,如果我们有适当的编码方法,就能将任何数学问题,包括它的初值和算法,变成一列符号串,写到初始的第一条格子带上。然后,根据细胞自动机内定的变换规则,可以得到下一时刻的符号串,也就是说,完成了一次“计算”。依此类推,时间不断地前进,“计算”便一步一步地进行,直到所需要的结果。这个过程,的确与计算机的计算过程类似。
但是,并非所有规则的细胞自动机,都能等同于真正的计算机,还得看看它的智商如何?上面说过,我们有256种不同规则的细胞自动机,它们的智商高低不同,各具有不同的“计算”能力,。
例如,让我们考查一下图(27.3)所显示的256个初级细胞自动机中的几个特例:
1. 首先,象“规则 255”这样的,完全谈不上什么计算能力,连“识别”能力都没有,因为无论对什么“数”,经它“计算”一次之后,全部一抹‘黑’,这点从它的规则定义也可看出来;“规则0”也一样,全部一抹‘白’。
2. 接着,我们再来看象“规则 90”那一类的,时间演化图有点象帕斯卡三角形的那种。这种情况的结果太规矩了,一个呆脑瓜,肯定计算能力有限,第一条的数据再复杂,犹如“对牛弹琴”一样。
3. 另外,象“规则 30”那样的,似乎较好一些,但逻辑杂乱无章,是个胡作非为、不听指挥的家伙。
4. 最后,唯有像“规则 110”这样的,计算能力才达到标准,被证明与通用图灵机是计算等效的。
…………
林童看完了有关‘初级细胞自动机’的介绍,闭着眼睛遐思冥想。王二没错!月亮的确不是木头做的,我们的世界也不能单靠计算而算出来。但是,分形、混沌、以及非线性科学中的这些数学模型,以及计算机迭代的方法,对理解大自然还是很有用处的。林童想,科学真是太有趣、太迷人了!科学就像一座美丽宏大的花园,从分形和混沌这几支科苑奇葩,他似乎看到了满园的绿草如茵、花果飘香。林童想着想着,不知不觉地进入了梦乡,梦中,他倘佯在百花丛中……
(全文完)
https://blog.sciencenet.cn/blog-677221-636232.html
上一篇:《走近混沌》-26-生命游戏-2
下一篇:“傻”博士的初恋-引子(读小说-猜画谜-轻松轻松!)
全部作者的精选博文
全部作者的其他最新博文
全部精选博文导读
相关博文
- • 热烈祝贺海南大学9位学者入选斯坦福大学顶尖科学家2024年Career榜
- • 祝贺访问学者吕改芳和研究生杨梦蝶等合作SCI论文在Colloids and Surfaces A发表
- • Relativity of Hallucination(初学者版)
- • Are Human Beings Living in a Hallucination?(初学者版)
- • Theory of Relativity of Hallucination by Yucong Duan(初学者版)
- • The "Emergence" of LLMs by Relativity of Consciousness(初学者版)