博文
一种节点组重要性排序方法
 精选
精选
|
一种节点组重要性排序方法
陆君安(武汉大学) 刘 慧(华中科技大学)
网络科学中关于节点重要性排序方法很多,譬如节点度(degree),中心度(K-shell)即核数(coreness),介数(betweenness),H-index,还有 Page-Rank等等。可是关于节点组(或者社团)的重要性排序方法几乎没有什么研究,事实上节点组重要性排序问题在现实中广泛存在。节点组重要性排序针对的不是单个节点,而是若干个节点组成的团和组。一批乒乓球运动员中如何组织双打队(节点数为2的节点组排序),是不是一定由单打冠亚军(单个节点排序的第一二名)组成的双打最强?一根水平樑如何选择两个(或者若干个)基点将它吊起?两块相同形状的材料加固时如何选择若干个加固点的位置进行加固?这样的问题在实际中常常遇见, 应对的方法一般是凭经验或者一些特殊办法。而我们通过研究提出了一个基于牵制控制的节点组重要性排序的一般方法,有数学理论的保证和算法的实现。这一方法的理论依据是我们最近发表在IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS: SYSTEMS上的文章Optimizing Pinning Control of Complex Dynamical Networks Based on Spectral Properties of Grounded Laplacian Matrices,作者:刘慧(华中科技大学),徐宣宏(华中科技大学),陆君安(武汉大学),陈关荣(香港城市大学),曾志刚(华中科技大学)[1]。

图1
我们发现复杂网络牵制控制与节点组重要性排序这个问题紧密联系,最重要的节点组完全由网络Laplacian主子矩阵的最小特征值决定。大规模复杂网络牵制控制的方法,是指只需要控制其中的一部分节点便能够控制整个大规模网络。选择牵制控制节点(组)的关键是受控网络Laplacian矩阵的删后主子矩阵最小特征值,就是将Laplacian矩阵删掉牵制控制节点(组)对应的行和列之后剩下的子矩阵(the grounded Laplacian matrix obtained by deleting the rows and columns corresponding to the pinned nodes from the Laplacian matrix of the network)的最小特征值,这也是牵制控制的关键,如果节点(组)对应的主子矩阵最小特征值越大则这样的节点(组)越重要,于是主子矩阵最小特征值也成为节点(组)重要性的指标。找出对全局具有牵一发而动全身作用的节点(组),控制这样的节点(组)能够用最小的代价达到整体的最佳效果,这样的节点(组)就是系统最重要的节点(组)。
看一个十分简单的例子。由5个节点组成的链,见图2,如何选择一个最重要的节点呢?第一步写出链的Laplacian矩阵L,按照删后主子矩阵最小特征值定义计算节点1(或者5)对应的最小特征值为0.1206, 节点2(或者4)对应的最小特征值为0.1981, 节点3对应的最小特征值为0.3820,因此这5个节点的链最重要的节点为3,其次为2和4,最后为1和5。
|
| ||
图2
那么5个节点组成的链如何选择两个最重要的节点呢?同样计算Laplacian矩阵删后两行两列的主子矩阵最小特征值,得到最重要的节点组是{2,4}{1,4}{2,5}(主子矩阵最小特征值为1),其次为{1,5}(主子矩阵最小特征值为0.5858),再其次为{2,3}{1,3}{3,4}{3,5}(主子矩阵最小特征值为0.3820),其它节点组{1,2}{4,5}最差(主子矩阵最小特征值为0.1981)。这样通过计算删后主子矩阵最小特征值,把两个节点组成的十种节点组的重要性进行了排序。
一根水平樑如何选择两个基点将它吊起呢?假设樑长度为1,然后作细等分(只要细分足够密,离散网络的节点组排序可以逼近连续问题的基点选择),分点视为节点,便成为N个节点的链。
图3中横坐标是节点编号,纵坐标是主子矩阵最小特征值,其中N=82,牵制第一个节点从1到41中选,另一个从82到42中选,当两个节点分别选取(21,62)时特征值取得最大值。当两个节点都取两端或者中间时,特征值达最小值。发现对于链状取两个控制节点情况,最优节点接近左右各1/4的位置。当N数量更大时,更接近1/4的位置,例如取N=302的链状 ,经计算,控制两个节点的最优组合为(76,227),符合上述1/4的规律。
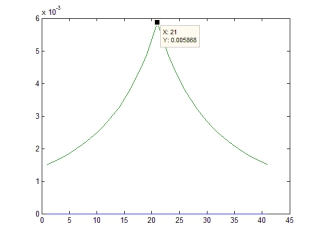
图3 主子矩阵最小特征值与选点位置(两点对称)关系图(N=82)
正方形网络控制两个节点情况
这时最优控制节点处于对称位置,却并不一定处于对角线上,见图4。
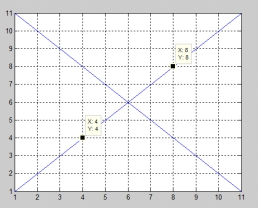
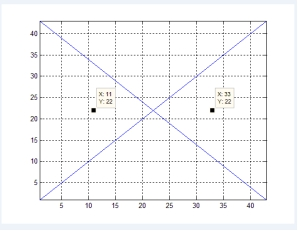

50*50
图4 正方形网络控制两个节点情况
正方形网络控制四个节点情况
这时大正方形网络分成四个小正方形网络,在四个小正方形找中心节点(可能在中心偏移一格的位置上),这个结论与方形2个节点的位置相通,见图5.


图5 正方形网络控制四个节点情况(40*40)
我们再来看一个有趣的例子,如图4的两个星形连接的网络,如果按单个节点排序,节点1最重要的(最小特征值0.1459),节点2和8第二重要(最小特征值为0.0750),而在两个节点的节点组重要性排序中,节点{2,8}组成的节点组最小特征值最大(最小特征值达到1),而节点组{1,2}的最小特征值仅为0.1459,远小于1,尽管它包含单个节点排序中最重要的节点1。说明单打冠亚军组成的双打不一定成为双打冠军。

图6 两个星形连接的网络
现在我们再来进一步分析,一个N个节点的网络,为了确定哪L个节点最重要,需要计算 个主子矩阵的最小特征值,当N很大时基本上是一个NP-Hard问题。为了减少计算量,我们在文献[1]中借助图谱理论给出一些重要定理,包括主子矩阵的最小特征值的上下界估计,提供了选点的指导,有的虽然不是最优的,也能够以比较小的计算代价,找到比较优的节点集。这里我们用到了200多年前的Cauchy 特征值交叉定理,它指出一个N阶对称矩阵和其N-1阶主子矩阵的特征值具有按顺序交叉不等关系。前不久华人数学家利用这个定理解决了困扰计算机圈近三十年的布尔函数敏感度猜想。请看下面一个例子。4个节点的图,对应的Laplacian矩阵的特征值为0,1,3,4,删去节点4后对应的Laplacian矩阵的特征值为0.4679,1.6527,3.879,满足交叉不等关系: 4>=3.879>=3>=1.6527>=1>=0.4679>=0.
个主子矩阵的最小特征值,当N很大时基本上是一个NP-Hard问题。为了减少计算量,我们在文献[1]中借助图谱理论给出一些重要定理,包括主子矩阵的最小特征值的上下界估计,提供了选点的指导,有的虽然不是最优的,也能够以比较小的计算代价,找到比较优的节点集。这里我们用到了200多年前的Cauchy 特征值交叉定理,它指出一个N阶对称矩阵和其N-1阶主子矩阵的特征值具有按顺序交叉不等关系。前不久华人数学家利用这个定理解决了困扰计算机圈近三十年的布尔函数敏感度猜想。请看下面一个例子。4个节点的图,对应的Laplacian矩阵的特征值为0,1,3,4,删去节点4后对应的Laplacian矩阵的特征值为0.4679,1.6527,3.879,满足交叉不等关系: 4>=3.879>=3>=1.6527>=1>=0.4679>=0.


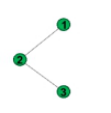

图7 Cauchy 特征值交叉定理的例子
最后我们再重新聚焦到Laplacian矩阵的删后主子矩阵最小特征值,非常有趣的是这个删后主子矩阵蕴含了原矩阵的隐藏信息,见图8。原网络A和B不同,删去节点4后相同,但是删后主子矩阵不同,特征值也不同,A和B的删后主子矩阵最小特征值分别为1和0.4679,说明节点4在网络A中比在网络B中更重要,这表明了删后主子矩阵及其特征值蕴含了原矩阵的隐藏信息。正如F.R.K. Chung(金荣芳院士)在 Spectral Graph Theory的Chapter 1中所说,谱图理论(Spectral graph theory)就像天文学家利用恒星光谱来确定遥远恒星的组成一样,我们要从网络的特征值谱中推演出网络的某些性质和结构。
A

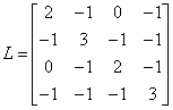 删去节点4后
删去节点4后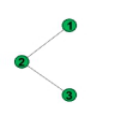
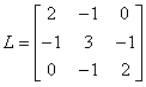

B
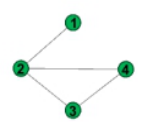
 删去节点4后
删去节点4后 


图8 删后主子矩阵及其特征值蕴含了原矩阵的隐藏信息
最后我们看一个500个节点的SF网络,利用[1]中的定理,不需要在N个节点中枚举便可以确定重要节点集。1个节点最佳为11,2个节点的节点组为{14,3}而不是{11,14},3个节点的节点组为{11,14,3},4个节点的节点组只要在度最大的25个节点中选取。

图9 (来自[1])
参考文献
[1]Hui Liu , Xuanhong Xu , Jun-An Lu , Guanrong Chen,and Zhigang Zeng, Optimal Pinning Control of Complex Dynamical NetworksBased on Spectral Properties of Grounded Laplacian Matrices, IEEE TRANSACTIONS ON SYSTEMS,MAN AND CYBERNETICS: Systems,Regular Paper,in press , 2019
http://blog.sciencenet.cn/home.php?mod=attachment&id=415495
[2]X. F. Wang and G. Chen, “Pinning control of scale-free dynamicalnetworks,” Physica A: Statistical Mechanics and its Applications, vol.310, no. 3, pp. 521–531, 2002.
[3] X. Li, X. Wang, and G. Chen, “Pinning a complex dynamical network to its equilibrium,” IEEETransactions on Circuits and Systems I: Regular Papers, vol. 51, no. 10, pp. 2074–2087, 2004
[4] J. Zhou, J.-A. Lu, and J. Lü, “Pinning adaptive synchronization of a general complex dynamical network,” Automatica, vol. 44, no. 4, pp.996–1003, 2008
https://blog.sciencenet.cn/blog-211414-1211599.html
上一篇:单打冠亚军组成的双打不一定成为双打冠军
下一篇:从复杂网络小世界,无标度, 高聚类特性看新型冠状病毒肺炎

