博文
压力消磁:电磁介质中功元的第五种形式 (II/II)
||
一, 引子
南京大学的邢定钰院士曾经说, 他发表过的唯一一篇教学研究论文是《外场中热力学系统能量和功的两种表述》(《大学物理》|1987年第2期|P.10-11|共2页)。足见电磁介质中功形式的重要性。邢先生大作采用的是通行观点:对于磁功元, 有如下两种形式
dW_1=HdM, dW_2=-MdH
注意, 对于稳恒场来说, 磁功和电功的形式具有对称性, 选择一种就可以了。本文主要讨论磁功的形式。
当时, 《大学物理》还比较“高端”, 文章没有摘要部分, 也没有引用部分。文章的第一段, 基本是全文的概要,抄录如下:
“在热力学和统计物理教科书中, 处于外电场中电介质系统(或处于外磁场中磁介质系统)的热力学第一定律的数学表述采用两种不同形式
dU1=dQ-pdV + EdP (HdM) (1)
dU2=dQ-pdV -PdE (- MdH) (2)
通常热力学部分用(1)式, 而统计物理中大多用(2)式。在这两种形式中, 功具有不同表达式, 系统能量也含有不同的物理意义。为了区别起见, 我们分别用U1和U1表示这两式中的能量。能量守恒定律为什么会有两种不同表述?这常使初学者感到困惑不解。本文以外电场中的电介质系统为例分析这两种表述的由来,差别以及它们之间的联系, 所有讨论也完全适用于磁场中的磁介质系统。”
中文《热力学与统计物理》教材并不多, 两部半来自南京大学,分别是龚昌德先生的《热力学与统计物理学》和欧阳荣百先生的《热力学与统计物理》,秦允豪先生的《普通物理学教程 热学》算半部。邢先生是《热力学与统计物理》教学和研究的专家, 现任全国热力学与统计物理教学研究会的副主任,不仅讲授该课多年,而且曾经参与龚昌德先生的《热力学与统计物理学》教材的完善。后面这一点写在龚先生教材第一版的序言中, 参见下图。

磁功元具有两种形式, 不仅仅是邢先生的看法,也是国际物理学界“最概然”的回答。磁功元当然可以还有其它的形式,不过知之甚少。
二, 均匀磁化介质中的总磁能是不是(1/2)HBV?
关于压力消磁, 我和热力学与统计物理学界的前辈沈抗存教授有一些讨论。沈先生头脑很清晰, 思辨锋利。但是他双耳有些失聪, 我们交流有些不顺畅,是我一时抓不住他思辨要点的关键原因。
---
先生明年步入九零后,按旧俗, 祝贺九十大寿正当时。祝先生福如东海, 青春永驻。
---
我把他最近几次“笔谈”的草稿收集起来, 进行了细致的研究, 发现有个推理如下。
从一个电磁学中的思考题开始。
如果一块介质具有线性且各向同性,并已经均匀磁化,设介质的总磁矩为m, 外场为H。问, 此时介质的磁能为多少? 如果外场变化导致介质的总磁矩、体积都变化, 则磁能的变化几何?
问题似乎很简单, 答案分别是:
W=(1/2) HBV, ΔW= (1/2)Δ(HBV)
但是, 这两个显然的答案, 其实都有严重局限!
设最初的系统处于温度T_i, 磁能是
W(X_i;T_i)=(1/2) (HBV) _{ X_i;T_i }
其中X是磁参量,H、B和M,和体积V的集合。系统最后的X值固定为X_f, 但是温度T_f互不相同, 则系统的磁能
$ W(X_f;T_f)=(1/2) (HBV) _{ X_f;T_f } $
并不唯一。回头再来考察温度的第一个答案W= (1/2)HBV, 立即发现答案也并不唯一, 因此第二个答案ΔW=(1/2)Δ(HBV)也不唯一。假如系统还有其它一些参量, 例如极化强度等, 问题也可以用同样的方法进行分析,结论也类似。
如果认为答案W= (1/2)HBV和ΔW=(1/2)Δ(HBV)是正确的, 必须限定X之外的所有变量都不变,就不再是一个热力学问题,或者说磁功是一个过程量,只有热力学才能提供完整的描述。
因此问题的症结都在于, 从热力学的角度看, 在介质中磁能的建立依赖于过程。即使达到X相同的状态, 不同的过程, 外界输入的磁能是不同的;外界输入的磁能, 不见得都以磁能的形式存储到介质中。
三, 均匀磁化介质中的总磁能不总是HBV/2的若干启示
1, 很多人认为热力学基本方程可以写为
U=TS-pV+μN+(1/2) HBV
这个观点或可讨论。但是, 如果把TS解释为热能, 把(1/2) HBV解释为磁能, 则是不可接受的。
2, 热力学基本方程是微分式, 即
dU=TdS-pdV+μdN+dW
其中dW为非体积功或者化学功, 包含其它功例如电磁功等。积分形式的基本方程需要条件:所有的功必须以广延量为自变量。这个要求没有物理原理的基础,参考磁介质中的功元有四种形式和第五种形式。
3,磁介质中单位体积中的功元有四种形式(参见I. P. Bazarov, Thermodynamics (The Macmillan Company, New York, 1964) , p.109)
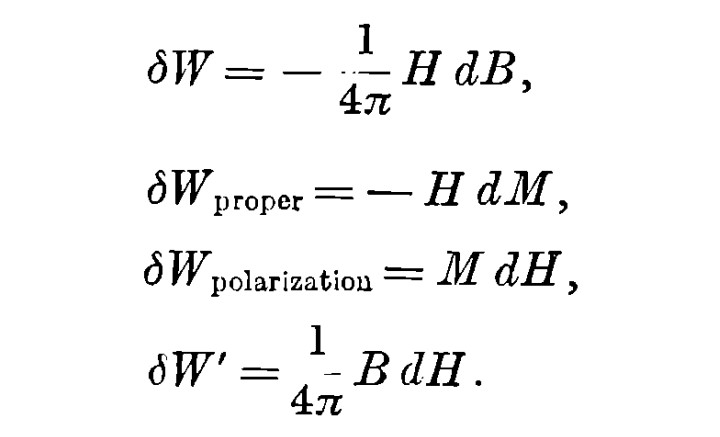
Bazarov对功的定义和我们通常的定义相差一个负号,另外他使用了高斯单位制,而非国际单位制。详细介绍这四种磁功的推导, 参考Bazarov的著作。
注意,这些磁功元中,自变量可以是广延量,也可以是强度量。
四, 磁介质中功的第五种形式
这一点, 必须回到电磁学或者电动力学, 注意其基本的表达式是微分式,参考下图(郭硕鸿《电动力学》(第三版,p.31))

也就是,单位体积中磁能元的表达式是dω=HdB,这里的单位体积是一个预先固定的量v,可以比介质的体积V小,也可以大,还可以一样。无论如何选取,这一块小体积内磁参量H、B和M必须是均匀的。dω=HdB是上面四种磁功元形式的出发点。
现在, 我们把一块介质作为热力学系统, 继续假设磁化的过程是可逆的。
1, 首先假定介质是均匀的, 在一个无限小的过程中, 保持绝热的条件下, 介质磁能的增加是
dW=Vdω (dω=HdB=(1/2) d(HB))
从微积分的角度, 这个公式的含义是,给定一个ω, 全部的体积V内都是同一个数值ω;不同的ω, 体积V是不同的;面积元是dW=Vdω。这和W=(1/2)HBV给出的结果不同。如果直接使用这个式子,得到的结果是,dW=Vdω+ωdV,而这是不对的,这个结果的的来暗含了W是状态量。
2, 如果介质是分块均匀的, 也就是
dW=∫dV(ω) dω
这个积分∫仅仅对体积进行。在简单的情况下, 这个积分容易处理, 在一般的情况下, 这个公式只有形式上的意义。传统的数学范畴内能不能处理这个积分? 不知道。不过,利用数值方法,总可以给出近似结果。
毫无疑问, 这种形式的磁功元dW, 是磁介质中功的第五种形式。谁首先使用了这种形式? 王竹溪!(参考下图中的公式(1)),也许还有Landau。

五, 磁介质中功的第五种形式的一个后果:压力消磁
如何从dW=Vdω出发获得压力消磁,已经讨论过很多次。有兴趣者可阅读论文:
文章下载网址
延展阅读
国内同行的压力导致我们决定尽快发表压力消磁这个新效应(I/II)
https://blog.sciencenet.cn/blog-3377-1430016.html
上一篇:一位大学生的自我批判
下一篇:从海外"名人录"到"外籍院士"