博文
数据分析--拟合
||
数据分析--拟合
1.求根
二分法,牛顿法,简单迭代法
newton法
迭代公式
F(X)的雅克比矩阵
2.最小二乘拟合
最小二乘拟合是将包含统计不确定性的数据拟合为公式(“理论”)的首选方法。
已知数据点(xi, yi), 在函数空间 中寻找S*(xi),使得
其中 是点xi 处的权
在连续空间C[a, b] 中选定 n+1 个线性无关基函数,由它们生成的子空间记为
线性拟合
若存在 ,使得
则称 为离散数据
在子空间
上的最小二乘拟合。
对于选定的基函数 ,拟合曲线
是n+1 个参数的线性函数,称之为线性最小二乘。
记然后要做的就是求 I 在极值点下的参数
通过求导寻找参数ak*
即
记m+1维向量:
用函数內积形式简记为
多项式拟合
其中 为权函数
实例
线性拟合
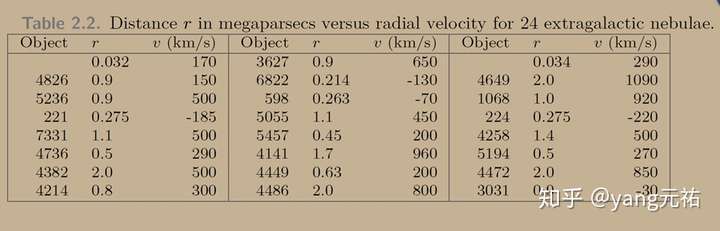
In 1929 Edwin Hubble examined the data in Table relating the radial velocity v of 24 extra galactic nebulae to their distance r from our galaxy. Although there was considerable scatter in the data, he fit them with a straight line:
对上面的数据做一个线性拟合
得到
y(x) = a0+a1 x a0 = 0.032 a1 = 0.9
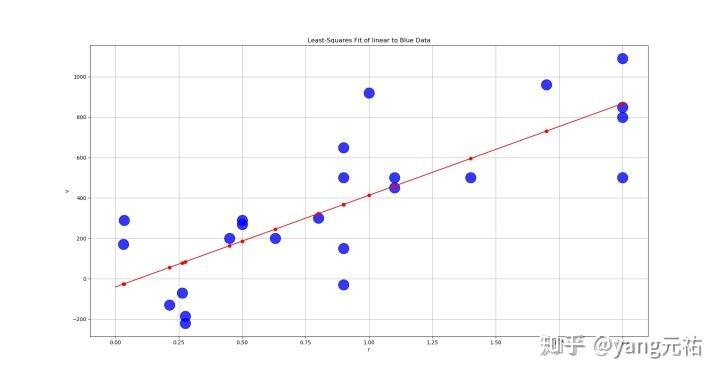
非线性拟合
下面采用洛伦兹函数来拟合数据
Measured total cross sections in millibarns of neutron-carbon scattering as a function of neutron energy in KeVs.

洛伦兹函数的形式
简记为
对三个参数的偏导数分别为
利用最小二乘得到
使用牛顿迭代法寻找参数
import math
import numpy as np
from numpy import *
import matplotlib.pyplot as plt
import matplotlib
plt.figure(figsize=(20,16), dpi=100)
plt.rc('font',family='Times New Roman')
matplotlib.rcParams['font.family']='STSong'
plt.rcParams['axes.unicode_minus']=False
matplotlib.rcParams['font.size']=20
ND=9
num =3
E=np.array([0, 13 ,25 ,38, 50, 63, 75, 87, 100])
S=np.array([10.6, 16.0, 45.0, 83.5, 52.8, 19.9, 10.8, 8.25, 4.7])
sig = np.ones_like(S)
#sig =np.array([9.34, 17.9, 41.5, 85.5, 51.5, 21.5, 10.8, 6.29, 4.14]) # Error bars
x = np.array([20000,40,220],dtype=float)
plt.plot(E, S, 'bo',markersize=20,alpha=0.4,label="采样数据点")
plt.title('Least-Squares Fit of linear to Blue Data',fontsize=20)
plt.xlabel('E',fontsize=32); plt.ylabel('$\sigma$',fontsize=32); plt.grid(True)
def Fun(x,num):
F = np.zeros((num),dtype=float)
for j in range(ND):
F[0] += (S[j]-x[0]/((E[j]-x[1])**2+x[2]))/sig[j]**2/((E[j]-x[1])**2+x[2])
F[1] += -2*x[0]*(E[j]-x[1])*(S[j]-x[0]/((E[j]-x[1])**2+x[2]))/sig[j]**2/((E[j]-x[1])**2+x[2])**2
F[2] += -x[0]*(S[j]-x[0]/((E[j]-x[1])**2+x[2]))/sig[j]**2/((E[j]-x[1])**2+x[2])**2
return F
def dfun(x,num):
df = np.zeros((num,num),dtype=float)
dx = 0.00001 #
x1_plus = np.copy(x)
x1_minus = np.copy(x)
for i in range(0,num):
for j in range(0,num):
x1_plus = np.copy(x)
x1_minus = np.copy(x)
x1_plus[j] = x1_plus[j]+dx/2 #x+dx
x1_minus[j] = x1_minus[j]-dx/2
df[i,j] = (Fun(x1_plus,num)[i]-Fun(x1_minus,num)[i])/dx #f(x+dx)-f(x)/dx
df_1 = np.linalg.inv(df) #计算逆矩阵
return df_1
def Newton(x,num):
x1 = np.copy(x)
i = 0
delta = np.copy(x)
# dfun0=dfun(x,num)
while(np.sum(abs(delta)) > 1.e-6 and i < 100): #控制循环次数
x1 = x-np.dot(dfun(x,num),Fun(x,num)) #公式
delta = x1-x
x = x1
i = i+1
print(x,)
return x
a = Newton(x,num)
print(a)
EX=np.linspace(0,100,1000)
G_E=x[0]/((EX-x[1])**2+x[2])
G = a[0]/((EX-a[1])**2+a[2])
points = a[0]/((E-a[1])**2+a[2])
plt.plot(EX, G_E,'k', linewidth=3.0,label="初猜曲线")
plt.plot(EX, G,'r:',linewidth=5.0,label="最终拟合曲线")
plt.plot(E, points, 'ro',markersize= 20)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.legend()
plt.show()results
[ 14956.38460591 38.99233378 177.84417855]
[ 16568.5542651 38.80318039 196.28768571]
[ 16786.04125645 38.81295456 198.89084396]
[ 16789.85161833 38.81293923 198.94072711]
[ 16789.85282055 38.81293926 198.94074454]
[ 16789.85282055 38.81293926 198.94074454]
[ 16789.85282055 38.81293926 198.94074454]
初值的选取很重要,因为在求解拟合参数时用的是牛顿法,如果选取的初值不合适则直接导致拟合参数不收敛,那就没法玩了。先把点描出来,然后根据洛伦兹函数估算出几个参数,首先是a2,a2是平方项(平方项说明它是对称函数)里面的,a2差不多就是平移量(40左右)。然后a3,a3差不多是半高宽一半的平方(200左右)。然后a1,a1是峰值(80)*a2,差不多是16000。
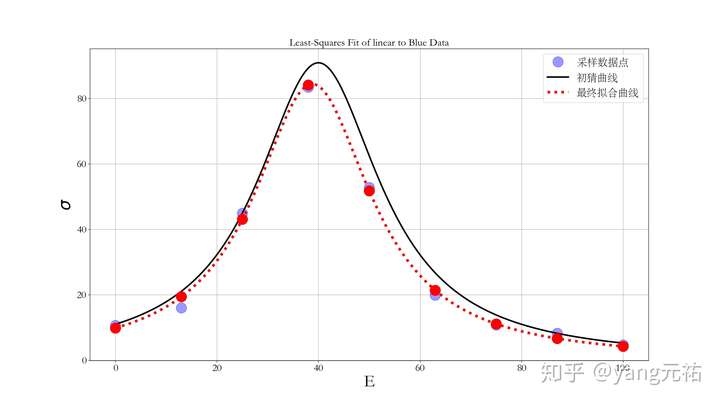
使用 scipy 库
import numpy as np
from scipy.optimize import leastsq
import pylab as pl
def func(x, p):
a1, a2, a3 = p
return a1/((x-a2)**2+a3)
def residuals(p, y, x):
return y - func(x, p)
x = np.linspace(0, 100, 1000)
p0 = [16000,40, 200, ]
x0=np.array([0, 13 ,25 ,38, 50, 63, 75, 87, 100])
y0=np.array([10.6, 16.0, 45.0, 83.5, 52.8, 19.9, 10.8, 8.25, 4.7])
y1 = y0 + 2 * np.random.randn(len(x0))
plsq = leastsq(residuals, p0, args=(y1, x0))
print (u"拟合参数", plsq[0])
plt.title(u'洛伦兹函数最小二乘法拟合',fontsize=20)
pl.plot(x0, y0, 'bo',markersize=20,alpha=0.4, label=u"真实数据")
pl.plot(x0, y1, 'y*', markersize=20,alpha=0.4, label=u"带噪声的实验数据")
pl.plot(x, func(x, plsq[0]), 'r:',linewidth=5.0, label=u"拟合曲线")
plt.plot(x, func(x, p0),'k', linewidth=3.0,label="初猜曲线")
plt.plot(x0, func(x0, plsq[0]), 'ro',markersize= 20)
plt.xlabel('E',fontsize=32); plt.ylabel('$\sigma$',fontsize=32); plt.grid(True)
pl.legend()
pl.show()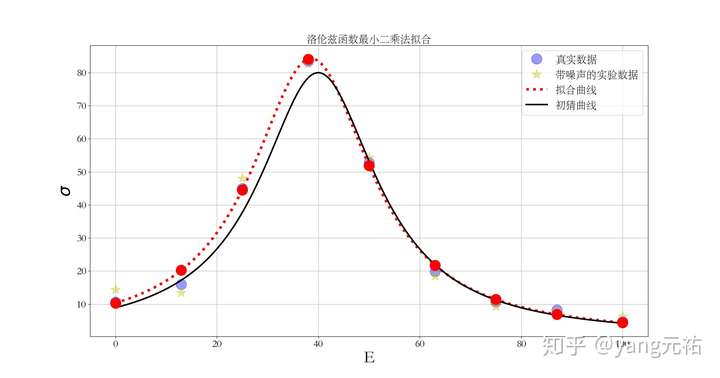
https://blog.sciencenet.cn/blog-566204-1173092.html
上一篇:计算物理——高斯积分代码
下一篇:无序系统晶格动力学 (综述文献简述)