博文
霍金与时间箭头之谜
 精选
精选
|||
今天是霍金逝世一周年,这是我在霍金逝世后不久写的一篇文章,贴出来作为纪念。本文刊登在《科学文化评论》第15卷,第2期,48-59页(2018)。
摘要:本文介绍了时间箭头问题(即时间为什么存在方向性)以及霍金对这一问题的研究。他最初开始进入宇宙学领域时首先对电磁学时间箭头问题进行了研究,他认为电磁学时间方向性的根源在热力学,而人主观感受的时间方向(心理学时间箭头)必然与热力学时间箭头一致,都是沿着熵增的方向。后来,在进行量子宇宙学研究时,霍金提出了无边界模型,在这一研究中霍金一度得出了宇宙膨胀时熵增加、宇宙收缩时熵减小的结论,但后来他认识到这一结论是错误的,并称之为自己在科学上的最大错误。
1. 时间的本质
提到霍金,即便是没有专业知识的普通公众也都听说过他撰写的《时间简史》(A brief history of time) 。作为霍金的第一本科普著作,这书名确实极为恰当:霍金本人的科学研究生涯正是从对时间箭头之谜的探究开始的,而终其一生,对时间问题的探索也始终是他研究的一个重要内容。
所谓时间箭头之谜,也就是时间为什么有方向的问题。自古以来,人们都用流水比喻时间,因为时间有一个特定的方向。在空间中我们可以向不同的方向运动,然而在时间中这是不可能的,我们只能随着时间“前行”,去往未来而无法返回过去,这是时间与空间的一个根本上的不同,也就是时间的方向性或者所谓时间箭头。为什么时间与空间会如此不同呢?是什么造成了时间箭头呢?自19世纪以来,这个问题就引起了许多科学家的思考。特别是,物理学上的许多基本的动力学理论,比如粒子的运动方程、电磁场的场方程等,都存在时间反演对称性:把方程中的时间t 变成 -t, 方程是不变的。例如,牛顿运动方程F=ma, 这里加速度a是位移的二阶导数,a=d2x/dt2, 如果我们把t 换成 -t, a是不变的,因此这个方程没有任何变化。既然如此,为什么我们能够区分过去和未来呢?这就是所谓时间箭头之谜。
据霍金本人回忆【1,2】,1960年代初他刚成为研究生的时候,导师夏玛(Dennis Sciama)给他的题目就与时间箭头问题有关。作为一个刚起步的研究生,霍金首先去图书馆查阅有关文献。不知是出于导师的建议还是他自己查询的结果,霍金想阅读的主要参考文献是哲学家赖欣巴哈(Hans Reichenbach) 的《时间的方向》(The Direction of Time)一书【3】。不过,霍金发现剑桥大学图书馆所藏的这本书被人借走了,登记的借书者是剧作家普莱斯特利(J. B. Priestley)。霍金在他的回忆中说,普莱斯特利借阅此书是为了写作他的戏剧《时间与康威一家》(Time and Conways)[1]。霍金相信该书中也许有他所想要寻找的答案,于是在图书馆填写了召回单,迫使Priestley把书还了回来。
这里顺便说说,《时间与康威一家》的主题也是对时间的理解【4】。在该剧第一幕中,康威夫人、女儿和儿子们以及孩子们的男友和女友们在家中开派对欢庆第一次世界大战的胜利结束,他们生活富足,充满了对未来的美好憧憬和希望,只有男孩Alan 似乎非常淡定。不过,在第一幕结束时,女孩Kay 却忽然有了一丝惆怅:她似乎在幻觉中看到了一些未来的情景。在第二幕中,同一地点,时间已过去了18年,然而生活却令人失望,每个人的婚姻、事业都未能如其所愿,一家的财富也已耗尽,被迫出售家庭房产,而且在种种经济困难中,一家人矛盾冲突不断,关系濒临破裂。只有Alan仍保持淡定。当Kay向Alan 谈起这些烦恼时,Alan 对她说,生活的秘密在于理解真正的实在:我们以为时光流逝、只能不断抓住机会尽量捞取眼前的东西,但其实这只是一种假象,如果我们能从永恒的角度来看问题,认识到每个人的一生其实就是时间空间中的一条轨迹,任何一个时刻只是我们自己的一个横断面,那我们就能超越我们的痛苦,也不必与别人发生冲突。第三幕又再回到当初:这时我们清楚地看到那时的康威一家就已播下了后来生活失败的种子,势利和傲慢扭曲了人们的心灵和关系。当派对结束时,Kay 似乎想起了她幻觉中看到的未来而感到一丝不安,她走出派对,Alan告诉她,将来他会帮助她。全剧结束。
这部戏剧通过一个人生故事,启发我们从另一个视角去审视时间的本质。实际上,把时间视为幻觉的看法由来已久。早在希腊时代,芝诺、巴门尼德等人就提出了飞矢不动、阿基里斯无法追上乌龟等关于时间的佯谬,进而主张真正的实在是超越于时间之外的【3】。爱因斯坦也表达过一种类似的看法。在一段悼念好友贝索的信中,他写道:“现在他又一次比我先行一步,离开了这个离奇的世界。这没有什么意义。对于我们有信仰的物理学家来说,过去、现在和未来之间的分别只不过有一种幻觉的意义而已,尽管这幻觉很顽强。”【5】不过,不可否认的是,过去与未来并不对称:对于过去,我们存有记忆而无法改变,对于未来我们则能够改变却无法预知。因此,就记忆或心理而言,时间的方向性是明显的,也就是存在所谓心理时间箭头。或者,反过来也可以说,我们能够根据记忆来定义时间的方向。
再回到赖欣巴哈的哲学书。赖欣巴哈本人也是学习数学和物理出身,曾在德国跟随爱因斯坦研究相对论,后来转入哲学,是逻辑经验主义学派的主要成员之一。他在这本书里,也回顾并评述了从古希腊哲学家到康德、柏格森等近代哲学家再到现代物理学中人们对于时间的种种思索和研究。赖欣巴哈把时间箭头的起源归结于因果性,并试图通过仔细的定义和分析“因”与“果”的差异给出时间箭头的起源。霍金后来说,他读了此书后大失所望,认为书的内容相当晦涩,而且在霍金看来,用因果性解释时间箭头是一种循环逻辑,因为在物理上的运动定律是对称的:过去的状态诚然可以决定未来的状态,但反过来也可以说如果未来的状态确定了,那么过去的状态也就确定了[2]。
2. 电磁学时间箭头
导师夏玛建议霍金阅读一篇由加拿大物理学家Hogarth撰写的最新论文【7】,研究另一种时间箭头的可能来源:电磁时间箭头或者叫辐射时间箭头。在电磁学中,电磁波方程是一种二阶微分方程,这种方程对时间是对称的,因此满足场方程的电磁波有所谓推迟解和超前解, 如果我们考虑一个电荷加速运动产生电磁波,那么应该选择推迟解,即电荷对周边电磁场的影响是经过一个时间Dt=r/c后传到距离电荷r处;但是求解方程的时候,还有另一种解,是距离r处的电场超前了Dt=r/c发生变化。为什么应选择推迟解而不是超前解? 通常的理解是这是由边界条件决定的:我们给定了电荷的运动,而并未假定恰好有从无限远处入射来的电磁波。
不过,1940年代,费曼(Richard Feynman)在攻读博士学位时和他的导师惠勒(J A Wheeler)提出的一种电磁理论表述为研究这一问题带来了新的视角,他们的理论称为直接作用电磁理论【8,9】。在这种表述中,并没有我们一般所说的电磁场,而只有电荷之间的相互作用。比如,我们看到太阳光,通常的理解是太阳上的电荷发生的热运动影响了周围的电磁场,产生了光波,传到我们眼中,导致眼中的电荷运动,于是阳光就被我们看到了。然而在直接作用理论中,并没有电磁场,而是太阳上的电荷与我们眼中的电荷有直接的吸引和排斥作用,这种作用会按照光速传播,它们的运动导致我们眼中的电荷感受到变化的相互作用,从而看见“阳光”。费曼之所以提出这种理论,是因为他当时认为导致量子电动力学中出现无限大的原因是点电荷的自相互作用【10】。如果没有电磁场,每个电荷都不会发生自相互作用,也许就可以避免这些无限大。但是,实际上只有包括了电荷的自相互作用才能得到与观测一致的“辐射阻尼”。为了解释这一点,费曼的思路是,加速的电荷会直接作用在“吸收体”上,这些吸收体因此会产生加速运动,这些加速运动电荷再反过来作用在原来那个电荷上,从而产生等效的自相互作用,这样就可以解释辐射阻尼。但这样一来,就出现了两个问题:一个是,这样的辐射阻尼看上去会依赖于吸收体的性质(数量、电荷、距离等等),而在电磁场理论中则与这些无关;还有一个问题:这些作用如果按照光速传播,将会延迟一段时间才能反作用在原来那个电荷上,而这与所要求的时间不一致。对第一个问题的解释是,如果吸收体数量非常多,分布在空间各个地方,那么最后结果就与其具体性质无关了。对第二个问题,惠勒和费曼发现,如果假定这种作用不是单纯的推迟解,而是一半推迟解,一半超前解,就正好可以获得所需的效果。使总的效果等效于我们通常所说的电磁波推迟解,这就为理解电磁时间箭头的出现提供了一种新的视角[3]。
Hogarth研究了把直接作用理论推广到膨胀宇宙的情况。这令当时的一些宇宙学家包括霍金的导师夏玛以及同在剑桥的霍伊尔(Hoyle)很感兴趣。霍伊尔是当时最著名的天文学家之一, 霍金去剑桥大学读研究生时本想申请霍伊尔作为导师【1】,但因为霍伊尔的学生已经太多未能如愿,而被分配给了此前他从未听说过的夏玛。事后看来,这真可谓塞翁失马焉知非福,尽管个人学术成就不如霍伊尔,但夏玛却是位极好的导师,他培养了包括霍金在内的许多极其优秀的研究生,其中很多人后来的名气都远远超过他自己。霍伊尔是稳恒态宇宙学理论的主将,稳恒态宇宙学理论认为宇宙在膨胀的同时也不断产生新的物质,从而一直保持相同的状态,这样的宇宙是无始无终的,不必象大爆炸宇宙学那样有个时间的起点。实际上,大爆炸宇宙学这个名字就是霍伊尔起的,本来大爆炸理论创始人勒梅特和伽莫夫等把他们自己的理论称为“原始火球理论”,后来在一次英国广播公司(BBC)的科普讲座中,霍伊尔略带嘲讽的把这一理论称之为大爆炸理论(Big Bang Theory),后来被普遍采用。霍伊尔和他的学生纳里卡尔(Nalikar) 把直接作用电磁理论用于膨胀宇宙,他们提出宇宙若象稳恒态宇宙学所主张的那样一直膨胀同时维持密度不变,则也能得到这一结果;反之,如果宇宙大爆炸,则不能得到这一结果,这被他们视为稳恒态宇宙的又一“证据”【11】。
霍伊尔后来在皇家学会做了这一理论的演讲,但在提问时,坐在听众席中的霍金却指出了霍伊尔和纳里卡尔理论存在问题【1,2,12】。霍伊尔说,“你怎么知道的”?霍金说他做了这一计算。很多听众以为霍金是当场心算得到这一结果的,实际上霍金与纳里卡尔共用办公室,他事先知道霍伊尔和纳里卡尔的工作情况。霍伊尔勃然大怒:此时他正在争取让剑桥大学为自己成立一个新研究所,他认为霍金当众指出自己论文中的问题可能是他的敌人故意安排的阴谋,想要出他的丑从而破坏他成立新研究所的努力。不过事后的发展证明,并没有这样的阴谋,他的研究所顺利成立,于是他与霍金的关系也就好转了,后来他还在研究所中给了霍金一个职位【2】。
其实,在这个问题上,费曼本人并不认可用电磁理论解释时间箭头的努力。费曼出席了1963年的一次关于这一问题的会议,在后来出版会议文集时,费曼认为该会上很多发言都是“胡话”(nonsense),不愿意把自己的名字与之联系在一起,因此坚持在该文集中不能提自己的名字,而只称为X先生(Mr. X)【13】。 X-先生明确指出,时间箭头的起源就是统计力学。实际上,惠勒和费曼曾与爱因斯坦讨论他们的这项工作,爱因斯坦告诉他们,之前他曾与Walter Ritz就电磁学时间箭头的起源进行过争论。Ritz认为,加速运动的电荷存在辐射阻尼表明电磁学中存在基本的时间不对称性,而爱因斯坦则认为,电磁学本质上是时间对称的,辐射阻尼实际上是由于电荷与大量其它电荷相互作用的平均效应,也就是时间箭头本质上来源于统计力学【14】。
3. 热力学时间箭头
我们知道有不可逆的热力学第二定律,随着时间的推移,封闭的热力学系统的熵总是增加的,这就是热力学上的时间箭头。这一定律的表现在日常生活中处处可见:把不同冷热的物体相接触,能量总是从热的一边传向冷的一边,而不会冷的越来越冷、热的越来越热;通过加热很容易把生米煮成熟饭,但是却没有办法把熟饭再变回生米,等等。那么,为什么热力学中存在不可逆性呢?热力学是人们根据宏观经验总结的物理学定律,它的微观基础是统计力学。在统计力学中,物质基本单元(原子或更基本的粒子)的微观运动本身对于时间可以是对称的[4],但是由于概率的关系,仍然会产生宏观的时间箭头。这种时间箭头的起源其实并不难以理解:一开始系统的粒子都分布在相空间中的一个小范围内,这就是所谓有序的或者叫低熵的初始态,随着时间推移,系统演化,从动力学的角度这些粒子的演化是确定的,但是如果不去求解动力学方程,那么在相空间中看它们的运动是随机的,只有某种概率分布。这些粒子在相空间中的轨迹逐渐分散开来。那么在未来的某一时刻,如果我们去看它们的分布,在绝大多数情况下,我们会看到它们在相空间中分布的范围比原来要大,也就是所谓无序的或者高熵的状态。如果拿我们日常生活中的例子来说明,假定你买到一副新扑克牌,打开盒子,你会发现牌是按照花色和大小排列好的。现在如果你随意“洗牌”,也就是随机地从其中拿出一些牌插到别的地方去,那么越“洗”这副牌的排列次序就越混乱无序。本质上,这与热力学第二定律中熵增加的原理是一样的。而且,在这一过程中,“微观过程”是可逆的,洗牌时你可以把前面的牌插到中间去,也可以把中间的牌抽出来放到前面去,这一过程是完全对称的,但只要你持续做下去,牌的次序就会越来越乱,直到完全打乱为止[5]。
用热力学时间箭头也很容易解释我们前面提到的心理时间箭头。虽然我们还不完全清楚大脑记忆是怎样工作的,但它应该是满足热力学第二定律的。另外,我们很清楚计算机的记忆是如何的工作的,而对计算机记忆的分析可以清晰地看到,要让计算机记录下任何东西,系统的总熵必然增加,因此这个心理时间箭头与热力学时间箭头完全一致,也许可以说是热力学时间箭头的方向决定了心理时间箭头。反之,设想有某个世界,其熵随着时间不断减少,那么根据它现在的状态可以给出其未来的状态,因此可以说它实际上有关于“未来”的记忆。所以,更确切地说,时间的方向是由热力学中熵增加的方向决定的【1】。
4. 宇宙学时间箭头
霍金在研究之后感到,时间箭头既然来源于热力学,在这一问题上难以取得更多进展,因此他暂时放下了这一问题。此时,伦敦的数学家彭罗斯(Penrose)对广义相对论的研究开始引起霍金的关注。彭罗斯使用几何方法,证明了黑洞时空中奇点的存在。霍金把这一方法应用到宇宙学上,发现宇宙中也不可避免地存在奇点,这为认可宇宙大爆炸提供了理论上的依据【2】。
70-80年代,正是量子宇宙学蓬勃发展的时期。随着宇宙微波背景被发现,大爆炸宇宙学理论被观测证实,学者们开始认真地思考令人不可思议的宇宙大爆炸之初的状态。霍金之前的研究表明,在宇宙的极早期,存在着理论上的奇点,也就是时空曲率达到无限大。不过,实际上在涉及的能量尺度达到了普朗克能标时,量子力学效应和万有引力效应都非常重要,因此量子引力可能会带来新的物理现象。遗憾的是,量子力学与描述引力的广义相对论作为现代物理学的两大基础,却一直未能融合,当时并没有一个自洽的量子引力理论。后来,弦论研究取得了很大进展,可能成为一个自洽的量子引力理论,但也还没有得到完全证明,更没有任何观测证据。尽管如此,人们还是试图在一定的限制条件(比如高度对称)下研究宇宙的量子效应。比如,在广义相对论中,时间和空间由度规张量描述,但广义相对论是个经典理论,度规张量是确定的。量子力学中,系统的状态则由波函数描述,其绝对值的平方给出了状态的几率分布。一种研究量子宇宙学的思路是,时空由度规张量所描述,可以写出度规的波函数及其满足的量子力学方程,也就是所谓惠勒-德维特(Wheeler-De Witt)方程,并在一定条件下求解。
霍金和哈特尔(James Hartle) 也尝试用这一方法研究宇宙极早期的量子过程【15】。他们使用了费曼的路径积分方法研究宇宙波函数。收到狄拉克的启发,费曼发现,可以用这样一种直观的方法理解量子力学系统的演化:系统从一个状态|A>到状态|B>的演化可以同时沿各种不同路径发生,每个路径产生一个不同的相因子,由该路径的作用量S给出,从状态|A>到状态|B>的跃迁振幅就是把这些不同的路径加起来。通常,这些相因子随着路径的微小变化剧烈变动,因此相互抵消。但是,在作用量S取极值的路径附近,所有路径的相位一致,因此不会抵消。而我们知道,系统的经典力学路径正是由这些S取极值之处,所以这就很好地用量子力学解释了经典力学。霍金和哈特尔把这一方法运用于量子宇宙学。为了便于计算,他们考虑了具有紧致三维几何的闭宇宙,而“路径”包括了所有没有边界的紧致四维流形,由于这些路径都没有边界,因此被称之为无边界的边界条件[6]。
在这一图像中,存在非常微小尺度上的量子时空涨落,通常它们无法直接形成按经典广义相对论膨胀的宇宙。但是,量子力学中有所谓隧道效应,这些涨落有一定的概率穿过势垒,最终形成膨胀的宇宙。有趣的是,从数学上看,当量子力学中一个粒子通过隧道效应穿越势垒时,时间是个虚数。因此,从物理世界的旁观者角度来看,粒子突然从势垒的一侧消失,而在势垒另一侧突然出现,但从粒子本身来看,这个过程却是连续的,只不过它在虚时间中穿越到了另一侧。类似地,在量子宇宙学中,并没有真正的奇点。这样,霍金就用量子力学,否定了他自己原来的宇宙开始时奇点不可避免的结论。另外,除了霍金和哈特尔模型外,还有一些其它类似但不同的解,例如Vilenkin 也给出了一个解,但与霍金-哈特尔解不同,他选取的边界条件是在半径R~0时产生的宇宙应该是一个纯粹膨胀的宇宙,称为“有生于无”(creation from nothing) 边界条件【16】。不过,到底怎样理解宇宙波函数、怎样选取边界条件、这些高度简化的模型到底在多大程度上准确反映了量子引力,这些目前都是还远没有定论的问题。
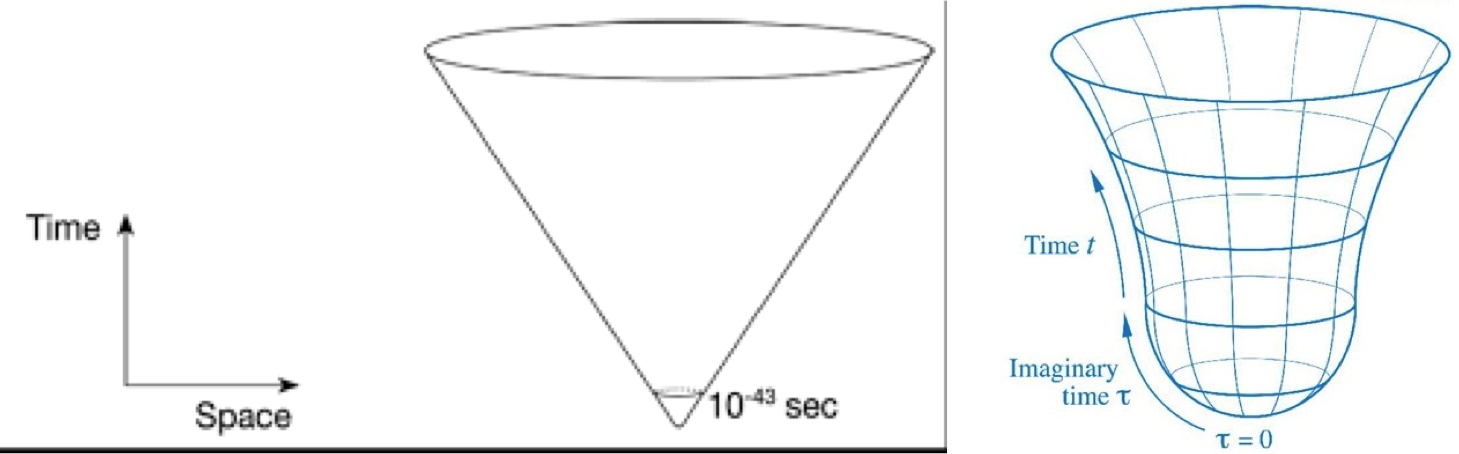
图1. 左:宇宙大爆炸示意图,有奇点,最下面10-43秒处量子引力变得重要。右:奇点被虚时间的连续时空代替,形成光滑流形。
回到时间箭头问题上来。除了热力学中的熵增加外,另一个明显的时间箭头是我们的宇宙在膨胀。这是偶然的呢?还是与热力学时间箭头联系着?我们为何生活在一个膨胀的宇宙中而非收缩的宇宙中?很多学者认为,包括热力学箭头在内的时间箭头都来自宇宙学,正是由于宇宙开始于熵比较低的状态,才能进而向熵更高的状态演化,从而允许有热力学的时间箭头。那么,如果宇宙由膨胀转为收缩,熵会如何变化呢?
霍金用他的无边界模型研究了宇宙膨胀到最大半径再转为收缩这一过程中扰动的变化【17】。假定这些扰动一开始很微小,当宇宙膨胀时,这些扰动会逐渐增大,熵也会变大。最初的计算似乎表明,当宇宙转为收缩时,这些扰动则会变小。因此,霍金认为,这表明宇宙膨胀和热力学时间箭头是联系在一起的:当宇宙转为收缩时,熵就会减小。但是,按照前面的讨论,心理时间箭头是沿着熵增的方向。因此,霍金提出了一种有趣的可能性:在这个收缩宇宙中如果有智慧生命存在,他们也不会发觉宇宙会收缩,相反,他们的时间认知将恰好反转过来,会把“前”与“后”逆转过来[7],因此也会认为自己的宇宙正在膨胀!当然,这里的一个问题是一个智慧生命如果生活在膨胀接近最大值的时刻,他会经历宇宙的膨胀-收缩过程,这时会发生什么?霍金推测,他会忘掉自己的过去,转而“记起”原来被认为是未来的东西。
这是一个听上去相当荒唐的情景。实际上,后来霍金承认,在与他的学生Don Page、R.Laflamme讨论后,他认识到在这里他犯了一个错误--他把这称作他自己最大的错误(my greatest mistake)。霍金说【19】,“当你发现自己犯了像这样的错误后应该怎么办?有些人从不承认他们是错误的,而继续去寻找新的往往相互不协调的论据为自己辩解--就像爱丁顿在反对黑洞理论时之所为;另外一些人首先宣称,从来没有主张过不正确的观点,如果主张过,也只是为了显示它是不协调的。在我看来,如果你在出版物中承认自己的错误,那会好得多,并可以减少混乱。爱因斯坦是个好的榜样,他为了建立静止宇宙模型而引入宇宙学常数,后来他把这称作一生中最大的错误”。霍金指出,之所以得到那些随着收缩变小的扰动,是因为选取了错误的边界条件。实际上,当宇宙开始收缩时,扰动仍会变大,熵也仍会继续增加【1】。因此,时间箭头从根本上来说是来源于热力学。在量子宇宙无边界模型中,可以预言宇宙开始膨胀,并在膨胀中熵增,但即使宇宙转入收缩阶段,熵仍然增加。至于为什么我们看到的宇宙是膨胀的?一种可能性是我们恰好处在这个阶段,另一种可能性是,到了遥远的未来宇宙开始转入收缩时,所有生命都早已在漫长的宇宙演化过程中衰亡,因此根据弱人择原理,我们看到的是膨胀宇宙。不过,应该指出的是,所有这些都是在无边界宇宙模型的框架下的讨论,实际上真实的宇宙未必就是由这一模型描述的。
5. 结语
时间的本质一直是令人极感兴趣但又非常难以把握的问题。作为时空理论的一位主要研究者,霍金在这方面也投入了许多时间精力,他的许多研究也别出心裁,并展现了深厚的功力。不过尽管如此,在这个领域中,他未能取得像奇点定理、黑洞热力学、霍金辐射等那样的重大成果,甚至还出现了错误。这恐怕是由于这一问题本身具有更大难度、更多不确定性造成的。
实际上,关于量子宇宙学的研究,在上世纪70-80年代取得了很大进步,霍金是其中的佼佼者。此后,一方面由于身体原因,他自己的研究工作变得更加困难,另一方面宇宙学的研究重点也发生了转移,宇宙学研究的主流转向了如何用实际观测检验理论模型,而抽象理论的研究也更多地转向与弦论/M-理论结合。霍金仍十分顽强地开展研究,虽然没有再取得他此前取得的那种重大成果,但直到去世前他一直活跃在研究的前沿上。
注释:
[1]这也许是霍金的主观猜测。实际上,普莱斯特利早在1937年就写出了《时间与康威一家》,远早于霍金到剑桥读研究生的1962年。而且,赖欣巴哈的遗作《时间的方向》一书是他去世后由夫人整理于1956年出版的,也晚于《时间与康威一家》的创作。不过,根据维基百科的介绍,普莱斯特利一直保持着对时间问题的兴趣,他的很多作品主题都与此有关,可能他因此借阅了该书。
[2]笔者个人阅读此书的感觉是,作为哲学著作此书并不算晦涩,甚至可以说是比较清晰明快的。虽然霍金在回忆中批评了此书,但其弟子Halliwell 也读了此书并对其有较好的评价【6】,可见霍金对此书也不是完全否定的。赖欣巴哈在此书中分析了因果关系,指出从可逆过程可以确认时间的有序性,但必须通过不可逆过程才能确认时间的方向性,而不可逆过程来自热力学。笔者猜测,令霍金感到失望是该书花了许多篇幅后才得到了的一些对霍金来说并不新奇的结论。
[3]惠勒和费曼的直接相互作用理论能够得到经典电磁场理论中的各种结果,但他们未能构造出相应的量子理论。后来,费曼、施温格(Julian Schwinger)、朝永振一郎、戴森(Freeman Dyson)等人构建了量子电动力学重整化理论,在通常的电磁场理论基础上解决了计算中出现无限大的问题。
[4]在弱相互作用中已发现存在时间反演不对称性,这种不对称可能是自发破缺形成的。但是统计力学中的时间不对称性并不依赖于这种微观时间反演不对称性,对于电磁相互作用、强相互作用等目前尚未发现微观时间不对称性的相互作用,同样可以产生宏观时间不对称性。
[5]仔细考虑这个问题我们会想到,在牌的排布已经变得很无序以后,如果继续无休无止地洗牌,偶然地也会碰巧使其变得有规律了一些,也就是熵减少了一些,这似乎和热力学第二定律相矛盾。但是,按照统计力学创立者玻尔兹曼(Boltzman)的解释,热力学第二定律严格地说是个统计规律,熵确实有可能自发地降低,只不过这种降低的概率远低于熵增加的概率,而且系统越大、熵减少的数量越大,这种概率就越低,对宏观系统来说这种概率低得不可思议,以至我们几乎永远都不会看到熵减少的情况。
[6]哈特尔本人后来指出,其实称之为单边界(one-boundary)的边界条件更为准确。
[7]有趣的是,我国古代哲学家惠施曾有“今日适越而昔至”的命题,由于缺乏更多资料,这一命题究竟是什么意思今天已很难考证。刘辽教授曾提出,惠施也许想到了时间旅行的可能性【18】。笔者认为,也有可能惠施思考了时间方向的问题。
参考文献
【1】S. Hawking, 1991, The No Boundary Condition And The Arrow of Time, in J. J. Halliwell, J. Perez-Mercader, W. H. Zurek eds., Physical Origin of Time Asymmetry, pp. 346-358, Cambridge University Press, 1994。
【2】S. Hawking, 2002, Sixty Years in a Nutshell, in G.W. Gibbons, E.P.S. Shellard, S.J. Rankin, The Future of Theoretical Physics and Cosmology, pp.105-117, Cambridge University Press, 2003.
【3】 H. Reichenbach, The Direction of Time, University of California Press, Berkeley, 1956.
【4】https://en.wikipedia.org/wiki/Time_and_the_Conways
【5】爱因斯坦,1955,给M. 贝索的儿子和妹妹的信,许良英、赵中立、张宣三译,《爱因斯坦文集》,第3卷,p.507, 商务印书馆,1979年第1版。
【6】J. J. Halliwell, 1991, Quantum Cosmology and Time Asymmetry, in J. J. Halliwell, J. Perez-Mercader, W. H. Zurek eds., Physical Origin of Time Asymmetry, pp. 369-389, Cambridge University Press, 1994。
【7】 J. E. Hogarth, 1962, Cosmological Considerisions of the Absorber Theory of Radiation, Proceedings of Royal Society, A267, 365
【8】Wheeler, J. A. and Feynman, R. P.,1945,Interaction with the Absorber as the Mechanism of Radiation. Reviews of Modern Physics, 17 (2–3): 157–181;
【9】Wheeler, J. A. and Feynman, R. P.,1949,Classical Electrodynamics in Terms of Direct Interparticle Action,Reviews of Modern Physics,21 (3): 425–433.
【10】Schweber, S. S., 1994, QED and the Men Who Made It, Princeton University Press.
【11】F. Hoyle and Narlikar, J. V., 1964, Time Symmetric Electrodynamics and the Arror of Time in Cosmology. Proceedings of the Royal Society A273, 1.
【12】Hawking, S. W., 1965,On the Hoyle-Narlikar Theory of Gravitation, Proceedings of the Royal Society A 286, 313.
【13】Gold, T. eds., 1963, The Nature of Time, Cornell University Press, 1967.
【14】Wheeler,J. A., 1991, Time Today, in J. J. Halliwell, J. Perez-Mercader, W. H. Zurek eds., Physical Origin of Time Asymmetry, pp. 369-389, Cambridge University Press, 1994。
【15】Hartle, J. B. and Hawking, S. W., 1983, Wave Function of the Universe. Physical Review D28, 2960.
【16】Vilenkin, A. 1982, Creation of the Universe from Nothing, Physics Letters B 117, 25
【17】Hawking, S.W., 1985, The Arror of Time in Cosmology. Physical Review D32, 2489
【18】刘辽,赵峥,田贵花,张靖仪,《黑洞与时间的性质》,北京大学出版社,2008.
【19】Hawking, S.W., 1988, A Brief History of Time: From the Big Bang to Black Holes
https://blog.sciencenet.cn/blog-3061-1167400.html
上一篇:人生如山岳
下一篇:玻尔和拉比纪念爱因斯坦的文章
全部作者的精选博文
全部作者的其他最新博文
全部精选博文导读
相关博文
- • AAA PCI -- 学者心声(Authorea 预印论文报道)
- • Building a DIKWP-TRIZ Software System (初学者版)
- • DIKWP-TRIZ: Semantic Blockchain and Semantic Communica(初学者版)
- • DIKWP-TRIZ in 3-No Problem and Artificial Consciousnes(初学者版)
- • Comparison Between DIKWP-TRIZ and TRIZ(初学者版)
- • DIKWP-TRIZ: Enpower AI/AC Innovation (初学者版)