博文
帕瓦罗蒂的声音为何能穿透交响乐队?
||
帕瓦罗蒂的声音为何能穿透交响乐队?
——声乐科学的200年革命与非线性声学新视角

马金龙
(中国科学院;长沙市老干部大学艺术团)
1987年,北京工人体育场的夜空下,帕瓦罗蒂在没有任何扩声设备的情况下,让数万名观众清晰听见每一个子音、每一次高C。那时,人们以为这是一种“天赋的神迹”。然而三十多年后的今天,声学、影像、神经科学与文化研究告诉我们:
帕瓦罗蒂的声音不是神话,而是一个由生理、声学、神经调控与文化结构共同组成的复杂系统奇观。
过去两百年间,声乐科学经历了四次重要范式跃迁,使这个曾被视为“不可言传”的艺术逐渐变得可观察、可测量、可建模。本文将简述这四次革命,并重点介绍过去十年快速兴起的 “歌唱的复杂系统—非线性声学视角”,以及它对解释帕瓦罗蒂“刀锋般穿透力”的潜在贡献。
本文的三个核心贡献:
l 系统梳理声乐科学200年四次范式革命
l 提出“歌唱五层复杂系统模型”
l 首次提出“歌唱准孤子”假说,为穿透力提供非线性声学解释

图1 四次范式跃迁时间轴
一、第一次范式革命(19世纪):喉镜开启“可见时代”
关键词:Bel Canto、喉镜(1854)、统一声区
在19世纪之前,歌唱教学高度依赖经验,以比喻为主要语言工具,例如:
“把声音挂在面罩里”
“让声音在头上空转”
“保持支点”
1854年,Manuel García发明喉镜,使人类第一次直接观察到声带振动。自此,声源机制从“想象”进入“可见”。
Bel Canto体系虽已极为成熟,但当时仍缺乏生理和物理层面的系统解释,因此难以完全复制与标准化。
二、第二次范式革命(20世纪中叶):线性声学模型奠定科学基础
关键词:声源—滤波器模型、共振峰、歌手共振峰
Gunnar Fant与Ingo Titze构建的Source–Filter Theory提供了现代声学框架:
声源:声带周期性振动 → 决定基频与泛音结构
滤波器:声道形状变化 → 形成不同共振峰(formants)
Johan Sundberg的研究进一步指出:
职业歌剧歌手在2.8–3.4 kHz区间存在一个额外能量峰(Singer’s Formant),其能量可比周围频段高出25–35 dB,使歌手的声音得以穿透大型交响乐队。
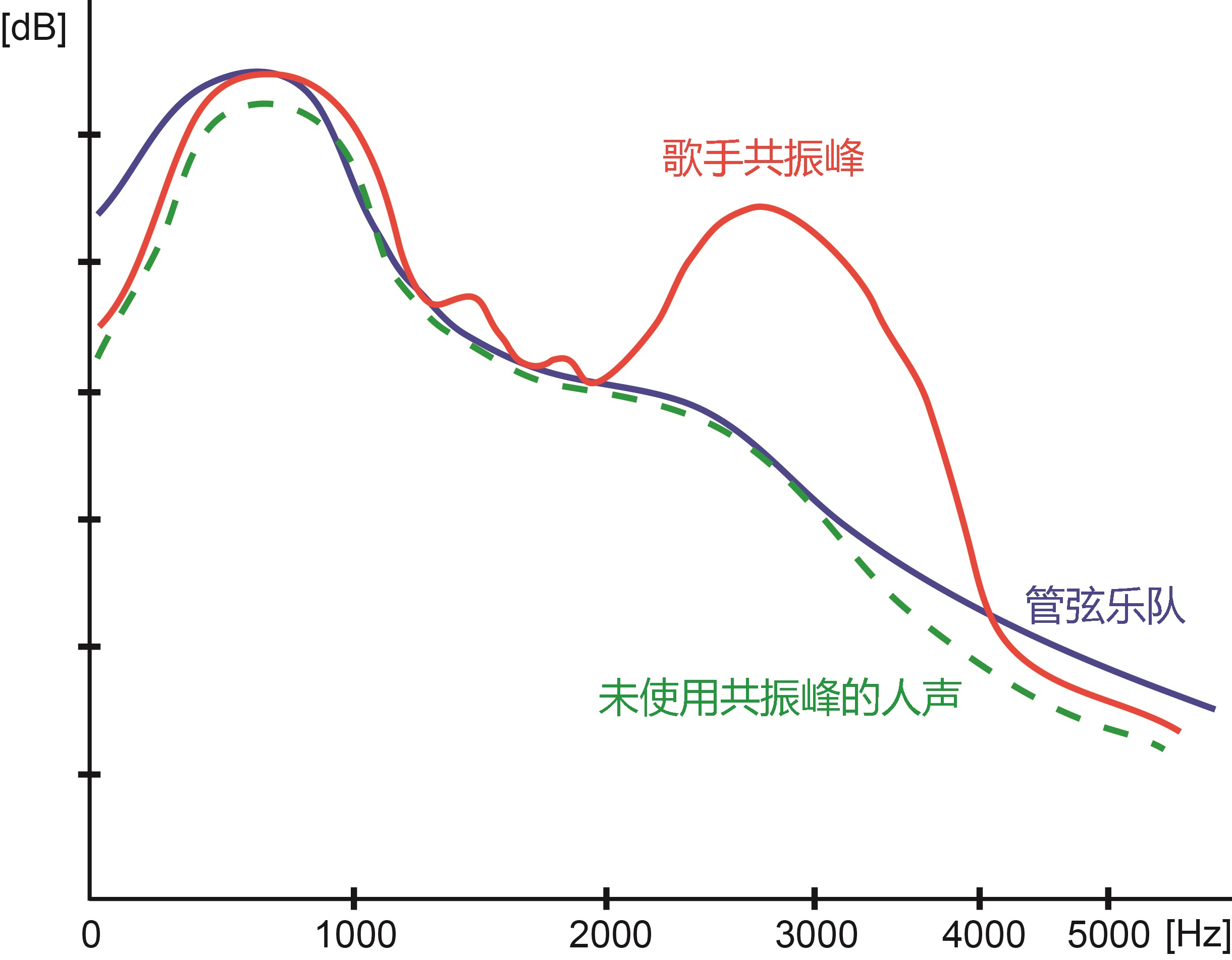
图2 歌手共振峰频谱图
虽然线性模型为声学奠定了基础,但其局限也显而易见:
难以解释强声区声门—声道的快速动态耦合
难以解释换声区的“突变”,这更像是动力学分岔
难以解释在相似参数下为何个体音色差异巨大
线性框架给予我们语言,但无法解释全部现象。
三、第三次范式革命(1980–2010):功能学派开启“参数化时代”
关键词:EVT、CVT、模块化、跨风格训练
随着流行、摇滚、音乐剧与民族唱法的崛起,传统美声难以涵盖所有声音需求。功能学派以“可控结构”作为核心理念:
EVT:13个可控结构
CVT:4类声带闭合模式
优势:
教学可重复性大幅提高
各种音色(嘶吼、哭腔、金属声)获得物理解释
声乐训练变得可操作、可标准化
局限:
过度参数化可能牺牲声音的整体性
重结构控制,轻动力学机制
对“声源—声道动态耦合”涉及较少
功能学派让声乐进入“可操作”时代,但尚未进入“系统时代”。
四、第四次范式革命(2010–至今):歌唱作为“复杂系统”
关键词:多层耦合、自组织临界态、非线性动力学
越来越多的研究指出: 歌唱不是线性叠加,而是一个典型的复杂系统。
本文采用作者整理的“五层系统模型”:
层级 | 核心机制 | 作用 |
物理层 | 非线性声波、能量局域化 | 音色核心、穿透力 |
生理层 | 呼吸—声门—声道协同 | 稳定性与动态范围 |
认知层 | 预测性听觉—运动闭环 | 精准度与灵活性 |
情感层 | 神经张力调制 | 情绪真实性 |
文化层 | 语言结构、美学吸引子 | 风格特征 |

图3 五层复杂系统框架图
传统“难以解释”的歌唱现象,在此框架下获得了新的解释:
换声区突变 → 系统跨越动力学分岔点
自然悦耳的声音 → 频谱呈现 1/f结构,自组织临界态
文化音色差异 → 风格作为文化吸引子
穿透力与音色核心 → 可能涉及声道局域化结构
此处不再将歌唱视为“零件叠加”,而是视为五层耦合的多尺度系统。
五、理论探索:非线性声学与“声波能量局域化”假说
线性声学可以解释Singer's Formant,却解释不了一个更极致的问题:
为什么3 kHz声波在100米外本应衰减殆尽,而帕瓦罗蒂的声音依旧刀锋般锐利?
本文提出一种理论假说: 杰出歌手的声道可能在17cm的长度内,通过非线性声学效应完成声波的“能量局域化预整形”,使声波在离开口腔的一瞬就拥有高度集中的能量结构——我们将这种现象称为“歌唱准孤子”(singing quasi-soliton)。
1.什么是声孤波?为何引入这个概念?
声孤波(acoustic soliton)是非线性声学中的一类特殊波动,具有以下特征(图4):
能量高度集中,不随传播距离散失
波形稳定,保持陡峭前沿
抗干扰性强,可穿透复杂声学环境
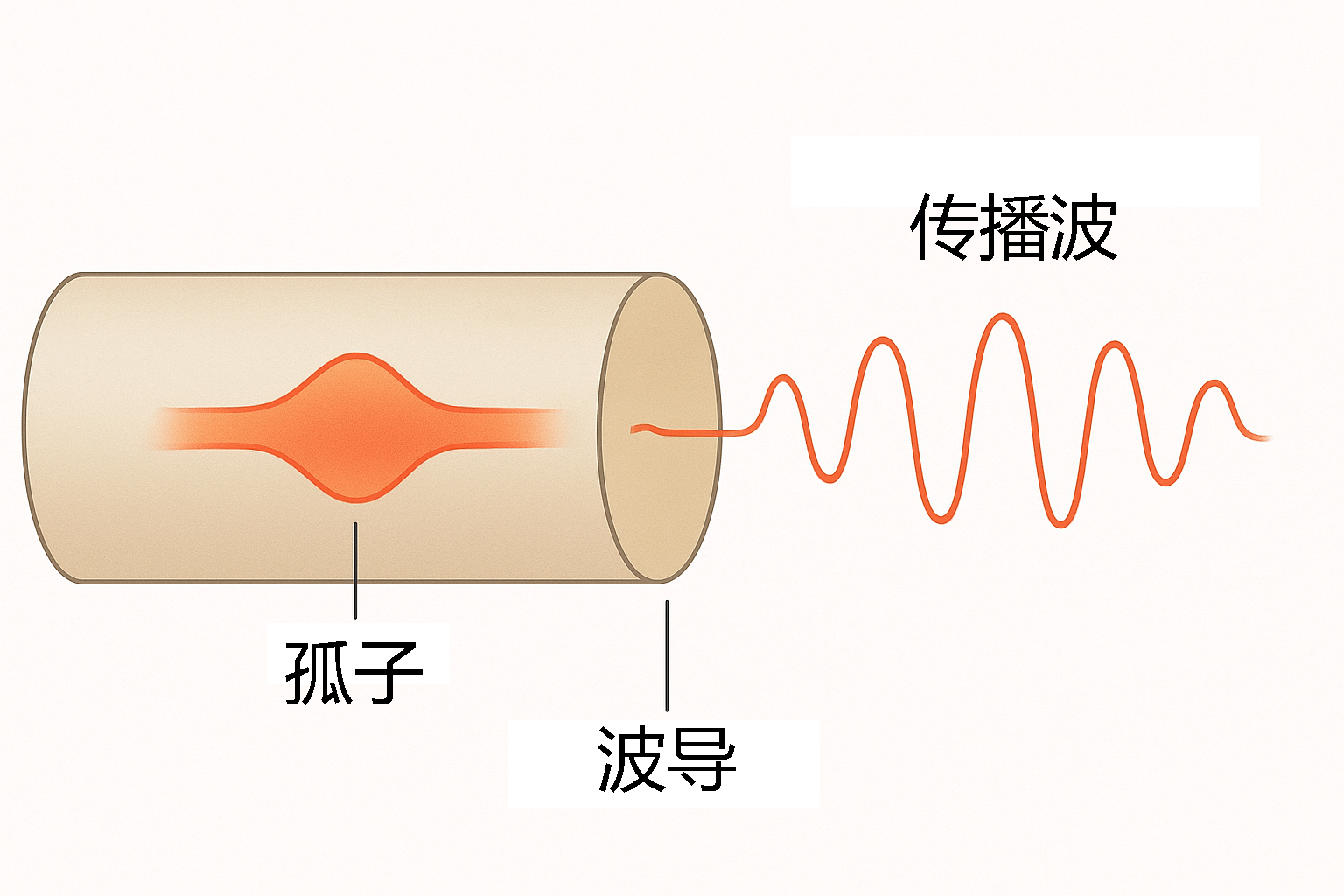
图4 声孤波概念图(示意图,非实测数据)
经典声孤波通常在强非线性介质(如气泡液体、颗粒材料)中,经过数米传播距离才能形成。人声道仅17 cm,且空气是弱非线性介质,理论上不可能形成严格意义的孤波。
但是,如果声道能够通过特殊的生理-声学结构,在短距离内实现类似孤波的能量集中效应,就可能解释杰出歌手声音的极端穿透力。
2.“准孤波预整形”的四个可能机制
我们提出以下四个机制可能协同作用,在声道内完成“准孤波”特征的初步形成:
(1) 声门“高峭度脉冲源”
职业歌手声带闭合速度可达1-2 m/s,形成陡峭压力脉冲,统计峭度(kurtosis)可达5-10。这种高峭度信号本身具备能量集中的初始条件,为后续非线性整形提供“种子”。
物理意义: 不同于正弦波源,高峭度脉冲在非线性传播中更容易形成能量局域化结构。
(2) 高Q值谐振腔的"等效传播增强"
声道Q值约15,意味着声波在腔内往返约15次才衰减。这相当于:
等效声学作用路径 ≈ 0.17 m × 15 = 2.5 m
虽然这不等同于几何传播距离,但高Q值环境会:
放大非线性相互作用时间
增强频率成分间的四波混频效应
促进能量向特定频段的再分配与集中
关键限定: 这不是真正的长距离非线性积累,而是通过多次反射实现的时间域非线性增强。
(3) 梨状窝的“频谱雕刻”功能
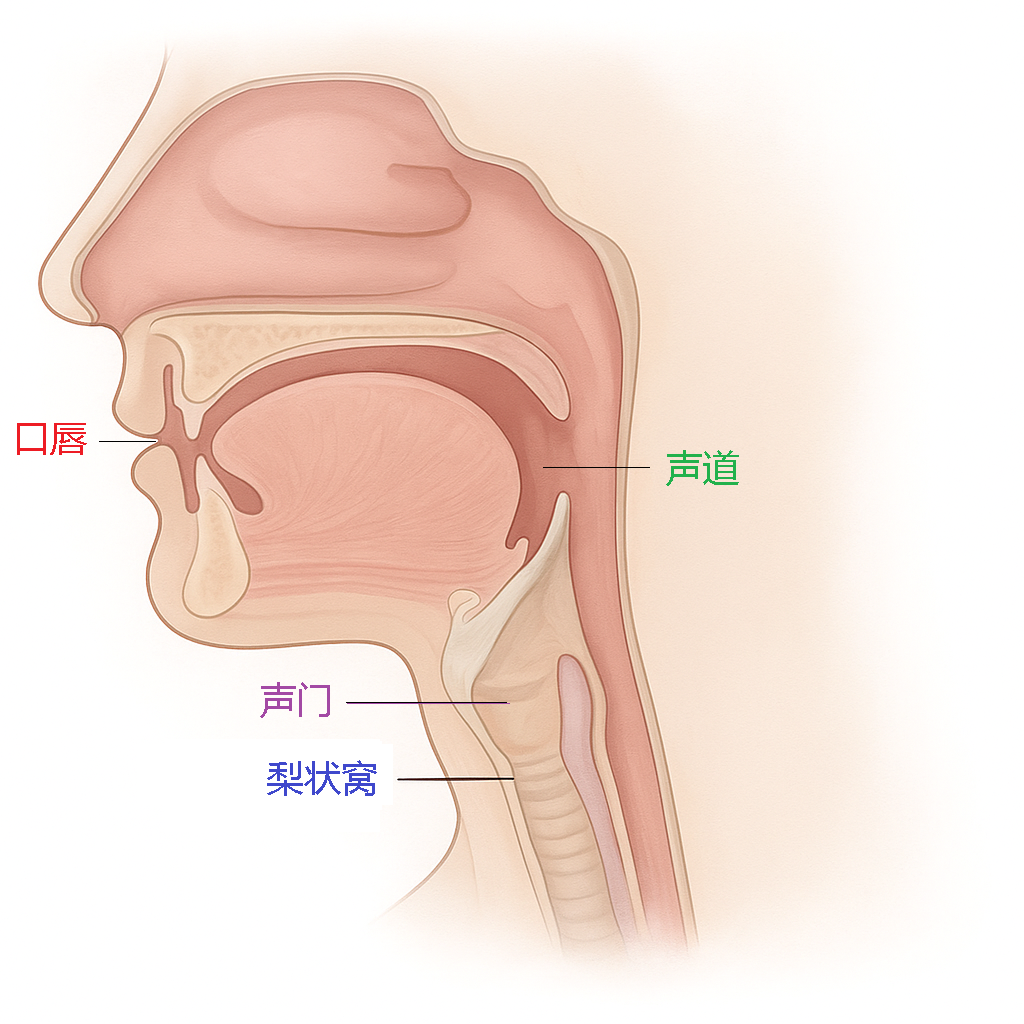
图5 声道解剖示意图
咽腔两侧梨状窝(pyriform sinuses)(图5)的3-4 kHz共振正好与Singer's Formant匹配,可能实现:
削弱过高频成分(>5 kHz)
提升3 kHz核心能量带
压缩频谱宽度,减少色散
物理类比: 类似光学中的带通滤波 + 色散补偿,为能量集中创造频域条件。
重要说明: 这主要是线性共振效应,但其产生的窄带高能量结构为非线性效应提供了更有利的初始条件。
(4) 口唇出口的“声学透镜”效应
声波离开口腔时,经历从低阻抗(口腔)到高阻抗(自由空间)的突变。经过前三个阶段整形的声波,在此界面可能发生:
非线性波前陡化(shock-front steepening)
能量向中心频段的最终聚焦
形成具有高方向性的辐射模式
结果: 声波离开口腔时已具备准孤波核心特征(图6):
✓ 陡峭前沿(steep wavefront)
✓ 高峭度值(high kurtosis,>5)
✓ 能量集中在3 kHz窄带
✓ 较强的抗色散能力

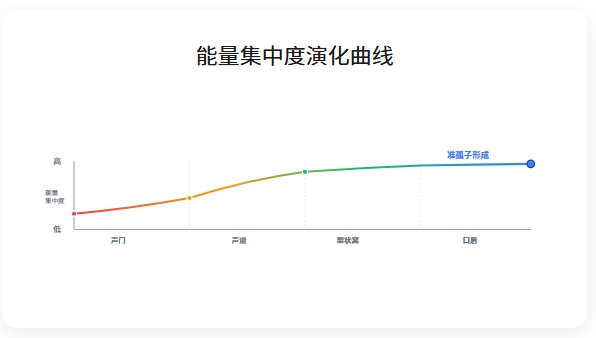
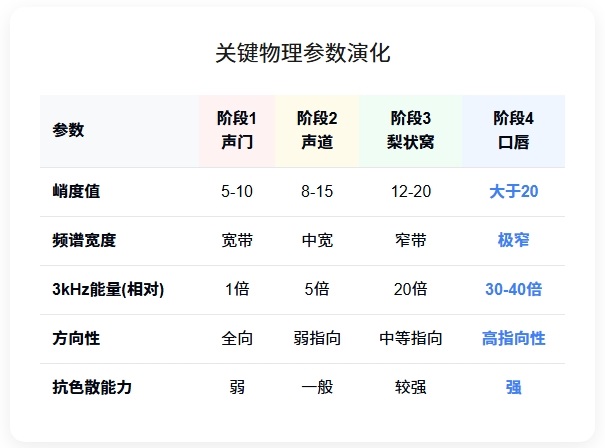
图6 准孤波预整形的四阶段示意图
图注:本图展示“歌唱准孤子”在声道17cm距离内的四阶段形成过程。
波形为概念示意,参数为理论预测值,尚需实验验证。
3.“歌唱准孤子”与经典孤波的区别
为避免术语混淆,我们明确区分:
特征 | 经典声孤波 | 歌唱准孤子(假说) |
形成环境 | 强非线性介质 | 弱非线性 + 高Q腔 |
传播距离 | 数米以上 | 17 cm短距离预整形 |
数学描述 | 严格满足KdV/NLS方程 | 近似满足,需修正模型 |
稳定性 | 碰撞后形状不变(粒子性) | 远场逐渐衰减,但比普通波抗衰减 |
物理本质 | 非线性与色散精确平衡 | 多机制协同的能量局域化 |
结论:“歌唱准孤子”是一种功能性类比,而非严格的孤波,但它捕捉了杰出歌手声音传播的核心物理特征。
4.可验证的六项预测
该假说虽为理论模型,但提出了可直接验证的预测:
近场峭度测量: 帕瓦罗蒂等顶级歌手的近场声压峭度应显著高于普通歌手(>8 vs <4)
梨状窝体积相关性: MRI测量梨状窝体积,应与穿透力评分呈正相关(r > 0.6)
Q值分布: 职业歌剧歌手声道Q值应集中在12-18区间
频谱演化: 用麦克风阵列测量0-50m声波演化,准孤子结构应表现出“核心频段能量衰减慢于边缘频段”
非线性参数: 声门处声压级>120 dB时,应可测到明显的二次谐波生成
跨文化对比: 意大利美声、京剧、蒙古长调等穿透力强的唱法,应具有相似的峭度与频谱集中特征
实验验证的技术路径:
目前的技术条件已基本具备验证条件:
声学测量: 高速麦克风阵列(采样率>96kHz)可捕捉峭度演化
医学影像: 3T MRI可精确重建梨状窝三维结构
声道建模: 有限元软件(COMSOL)可模拟非线性声传播
神经监测: 高密度肌电图(HD-sEMG)可追踪声门动态
建议的实验设计:对比研究3组被试(顶级歌剧歌手10名、职业歌手20名、非专业人士20名),在标准化声学环境下完整测量上述六项指标,并进行统计分析。
欢迎来自声学物理、医学影像、信号处理及声乐训练领域的同行共同验证或证伪。
5.理论意义与应用前景
若该假说得到验证,将具有以下意义:
科学层面:
建立声乐与非线性物理的桥梁
为“穿透力”提供可量化的物理指标
推动声道声学的精细化建模
应用层面:
智能训练系统: 实时监测峭度与频谱集中度,优化训练反馈
个性化声道优化: 根据MRI数据预测个体最佳共振配置
人工智能声音合成: 在TTS系统中模拟准孤子特征,提升合成音色的穿透力与真实感
当前假说的局限性:
简化假设: 将声道视为准一维管道,忽略了三维效应
个体差异: 模型未充分考虑解剖结构的个体变异
动态过程: 当前为静态分析,实际歌唱是高度动态的过程
文化因素: 听众对“穿透力”的感知可能受文化审美影响
这些局限提示我们需要更精细的多物理场耦合模型。
重要说明: 本节提出的“歌唱准孤子”是一个大胆的理论假说,目前尚无直接实验证据。其价值在于:
提供了超越线性声学的新视角
给出了可操作的验证方案
为跨学科合作搭建了概念框架
我们不声称这是唯一解释,也不排除其他机制(如听觉心理声学、声源指向性等)的贡献。科学的进步需要大胆假设,更需要小心求证。
六、未来方向:系统歌唱学(Systematic Vocalogy)
未来的歌唱科学可能沿以下方向发展:
实时神经—声学耦合的智能反馈训练
个体化吸引子寻优:每个人的“最佳临界态”并不相同
非线性声学应用:孤波、局域波、耦合振动机制
跨文化音色模型:语言结构 → 共振分布 → 美学吸引子
歌唱将从“经验艺术”迈向“可调控的复杂系统科学”。
七、结语
两百年来,人类逐渐从模糊的经验术语走向可观察、可模拟、可预测的科学体系。从歌手共振峰到换声区动力学,从情感表达的神经机制到非线性声波的系统耦合,歌唱比我们想象的更深邃,也更接近科学。
或许帕瓦罗蒂那一声划破剧院的九高C,并非“天赋奇迹”,而是在0.5毫秒内由声门、声道、神经调控、非线性声学与文化吸引子共同点亮的“复杂系统之光”。
期待更多来自声学、物理学、神经科学与声乐研究领域的同行,共同参与这一系统的深入探索与批评。
延伸阅读:
1. Sundberg, J. (1974). Articulatory interpretation of the "singing formant". The Journal of the Acoustical Society of America, 55(4), 838-844.
经典文献,首次系统阐述"歌手共振峰"的声学机制
2. Titze, I. R. (2000). Principles of Voice Production (2nd ed.). Iowa City: National Center for Voice and Speech.
声音产生原理的权威教材,Source-Filter理论的系统阐述
3. Fant, G. (1960). Acoustic Theory of Speech Production. The Hague: Mouton.
声源-滤波器理论的奠基性著作
4. Sundberg, J. (1987). The Science of the Singing Voice. DeKalb: Northern Illinois University Press.
歌唱声音科学的经典入门书籍
5. García, M. (1855). Observations on the human voice. Proceedings of the Royal Society of London, 7, 399-410.
喉镜发明者Manuel García的原始论文
6. Hirano, M. (1974). Morphological structure of the vocal cord as a vibrator and its variations. Folia Phoniatrica et Logopaedica, 26(2), 89-94.
声带微观结构研究的重要文献
7. Titze, I. R. (2006). The Myoelastic Aerodynamic Theory of Phonation. Iowa City: National Center for Voice and Speech.
发声的肌肉-弹性-气动理论
8. Estill, J., & Colton, R. H. (2012). The Estill Voice Model: Theory and Translation. Pittsburgh: Estill Voice International.
EVT (Estill Voice Training) 的理论基础
9. Sadolin, C. (2012). Complete Vocal Technique. Copenhagen: CVI Publications.
CVT (Complete Vocal Technique) 完整教程
10. Miller, R. (1986). The Structure of Singing: System and Art in Vocal Technique. New York: Schirmer Books.
美声唱法技术的系统性著作
11. Story, B. H., Titze, I. R., & Hoffman, E. A. (1996). Vocal tract area functions from magnetic resonance imaging. The Journal of the Acoustical Society of America, 100(1), 537-554.
使用MRI研究声道形状的开创性工作
12. Dang, J., & Honda, K. (1997). Acoustic characteristics of the piriform fossa in models and humans. The Journal of the Acoustical Society of America, 101(1), 456-465.
梨状窝声学特性的重要研究
13. Takemoto, H., Adachi, S., Kitamura, T., Mokhtari, P., & Honda, K. (2006). Acoustic roles of the laryngeal cavity in vocal tract resonance. The Journal of the Acoustical Society of America, 120(4), 2228-2238.
喉腔在声道共振中的作用
14. Hamilton, M. F., & Blackstock, D. T. (2008). Nonlinear Acoustics. San Diego: Academic Press.
非线性声学的权威教材
15. Enflo, B. O., & Hedberg, C. M. (2002). Theory of Nonlinear Acoustics in Fluids. Dordrecht: Kluwer Academic Publishers.
流体中非线性声学理论
16. Naugolnykh, K., & Ostrovsky, L. (1998). Nonlinear Wave Processes in Acoustics. Cambridge: Cambridge University Press.
声学中的非线性波过程
17. Rudenko, O. V., & Soluyan, S. I. (1977). Theoretical Foundations of Nonlinear Acoustics. New York: Consultants Bureau.
非线性声学理论基础
18. Zabusky, N. J., & Kruskal, M. D. (1965). Interaction of "solitons" in a collisionless plasma and the recurrence of initial states. Physical Review Letters, 15(6), 240-243.
"孤子"(soliton)一词的首次使用
19. Sugimoto N. et al. (1999). Nonlinear Acoustic Solitons and Shock Waves in Biological Tubes[J]. The Journal of the Acoustical Society of America. 106(4): 2173–2180. (nonlinear progressive waves)
在空气中的非线性前进波——声孤波
20. Engelbrecht, J., Salupere, A., & Tamm, K. (2011). Waves in microstructured solids and the Boussinesq paradigm. Wave Motion, 48(8), 717-726.
微结构固体中的波动与孤波
21. Christov, C. I., Maugin, G. A., & Velarde, M. G. (2007). Well-posed Boussinesq paradigm with purely spatial higher-order derivatives. Physical Review E, 54(4), 3621-3638.
孤波形成的数学模型
21. Bak, P., Tang, C., & Wiesenfeld, K. (1987). Self-organized criticality: An explanation of the 1/f noise. Physical Review Letters, 59(4), 381-384.
自组织临界态理论的奠基论文
22. Lucero, J. C., & Koenig, L. L. (2005). Simulations of temporal patterns of oral airflow in men and women using a two-mass model of the vocal folds under dynamic control. The Journal of the Acoustical Society of America, 117(3), 1362-1372.
声带动力学模型
23. Herzel, H., Berry, D., Titze, I. R., & Saleh, M. (1994). Analysis of vocal disorders with methods from nonlinear dynamics. Journal of Speech, Language, and Hearing Research, 37(5), 1008-1019.
用非线性动力学方法分析声音障碍
24. Guenther, F. H. (2006). Cortical interactions underlying the production of speech sounds. Journal of Communication Disorders, 39(5), 350-365.
发声的神经控制机制
25. Hickok, G., & Poeppel, D. (2007). The cortical organization of speech processing. Nature Reviews Neuroscience, 8(5), 393-402.
言语处理的大脑皮层组织
26. Tourville, J. A., & Guenther, F. H. (2011). The DIVA model: A neural theory of speech acquisition and production. Language and Cognitive Processes, 26(7), 952-981.
DIVA模型:言语习得与产生的神经理论
27. Sundberg, J., Prame, E., & Iwarsson, J. (1996). Replicability and accuracy of pitch patterns in professional singers. Phonetica, 53(4), 243-253.
职业歌手音高模式的可重复性
28. Cleveland, T. F., Sundberg, J., & Stone, R. E. (2001). Long-term-average spectrum characteristics of country singers during speaking and singing. Journal of Voice, 15(1), 54-60.
不同唱法的频谱特征比较
29. Bloothooft, G., & Plomp, R. (1986). The sound level of the singer's formant in professional singing. The Journal of the Acoustical Society of America, 79(6), 2028-2033.
职业歌唱中歌手共振峰的声级
30. Titze, I. R., & Story, B. H. (2021). Toward a consensus on symbolic notation of harmonics, resonances, and formants in vocalization. The Journal of the Acoustical Society of America, 149(5), 3290-3297.
发声中谐波、共振和共振峰符号标记的共识
31. Echternach, M., Sundberg, J., Arndt, S., Breyer, T., Markl, M., Schumacher, M., & Richter, B. (2010). Vocal tract in female registers—A dynamic real-time MRI study. Journal of Voice, 24(2), 133-139.
使用实时MRI研究女性不同声区的声道
32. Švec, J. G., & Schutte, H. K. (2012). Kymographic imaging of laryngeal vibrations. Current Opinion in Otolaryngology & Head and Neck Surgery, 20(6), 458-465.
喉振动的影像学研究
33. Maxfield, L., Patel, S., Yan, Y., Gartner-Schmidt, J., Jiang, J. J., & Smith, L. (2017). Quantifying the loss of acoustic energy in the human vocal tract: Measurements and modeling. The Journal of the Acoustical Society of America, 141(3), 1999-2007.
人声道中声能损失的量化
34. 韩德民, 徐文. (2015). 嗓音医学. 北京: 人民卫生出版社.
国内嗓音医学权威教材
35. 石惟正. (2002). 声乐学基础. 北京: 人民音乐出版社.
声乐教学的基础理论
36. 管谨义. (1997). 歌唱的艺术. 上海: 上海音乐出版社.
中国传统声乐教学经验总结
https://blog.sciencenet.cn/blog-312-1512408.html
上一篇:后记:写给未来的歌唱者