125. 粒子物理学的标准模型是否建立在坚实的数学基础之上？

Does the Standard Model of particle physics rest on solid mathematicalfoundations?

  题记：近 70 年以来，建立在“量子杨-米尔斯理论”之上的标准模型将粒子行为与几何中发现的数学结构巧妙地联系在一起。虽然这一理论数学上显得极其优雅和实用，但至今无人能证明它就是数学严密且物理真实的标准模型。

在杨振宁先生去世之前没能将第125个科学问题彻底解读完的遗憾来自于自己认知上的缺陷，在标准模型所展现的数学基础面前自己以往的知识显得非常匮乏，这个问题其实是一个非常宏大的科学问题，包含了关于杨-米尔斯理论的数学基础和标准模型及其未来的发展等诸多的数学和物理的问题，随着量子规范场理论的深入更多专业和晦涩的东西在我眼前展开，感到这一眼望不到边界的场景不是我能够在短时间内把握的，但为了完成这125个问题的解读，也为了纪念杨先生的个人愿望，我只能尝试着去科普一下这 125 个科学问题的最后一个科学问题，不当之处在所难免，敬请理解。

1. 杨-米尔斯规范场理论

首先我们简单介绍一下杨米尔斯理论和标准模型，才能明白它是否建立在坚实的数学基础之上，才能理解它是否可以用来理解真实的物理世界，虽然答案可能现在并不完全明确。杨-米尔斯理论(Yang-Mills theory)，又称非阿贝尔规范场理论，现在是描述自然界基本相互作用 (电磁、弱、强相互作用)的核心理论框架，也是粒子物理学标准模型(Standard Model)的数学基础。然而杨-米尔斯理论的诞生和任何一个成功的理论相似都是在旧理论的启发下，通过猜测、推广、完善才逐步确立而被主流科学所接受。

在20世纪50年代左右，当时最为成功的理论“量子电动力学(QED)”可以非常精确地计算电磁相互作用中的所有现象和过程，它成功地将量子力学与狭义相对论及电磁场理论统一起来，系统描述了光与物质相互作用的基本过程，其中非常著名的费曼图(Feynman diagram)就诞生在这里。虽然这个理论的数学基础似乎并不那么严格，比如其理论计算需要依赖微扰展开(不同阶的费曼图)，早期在计算高阶微扰项时就出现了所谓的“发散困难”(如在计算电子自能和真空极化等物理量时)，但QED成功引入了重整化(Renormalization)方法，将计算中出现的无穷大吸收到物理观测量的重新定义中(如电子自能发散部分应该收敛对应于电子的裸质量或裸电荷，这是由于电荷的电磁相互作用具有源奇点的缘故)，使得该理论成为电磁相互作用领域内最为精确和成功的理论，QED理论计算和实验测量的高度一致性使得费曼、施温格和朝永振一郎因发展重整化方法而共同获得1965年诺贝尔物理学奖。

尽管QED这个在计算上看似不怎么严格的理论(费曼图和路径积分展开)，却在理论完善上引入了规范场和规范变换的概念，这就是1928年由德国数学和物理学家外尔(Hermann Weyl)引入描写电磁场的规范理论，后来成为QED理论的核心。QED理论的核心是要求电子场ψ(x)在作局部U(1)相位变换ψ(x) → e^iϕ(x) ψ(x)下，系统拉格朗日量 L 保持不变。为了满足这一对称性要求，理论上必须引入一个规范场 A_µ(x) 做为补偿，因为相位变换在规范不变的要求下，必然会产生对应的规范场。QED理论的数学表达基于如下的拉格朗日量(下面统一采用爱因斯坦求和约定)：

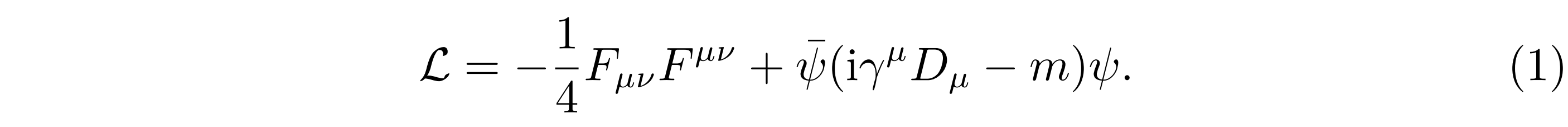
式 (1) 的第一项就是著名的麦克斯韦方程组的张量形式，F_µν就是电磁场的强度张量，它描述了自由电磁场的电磁场能量密度，由电磁场的四维矢势A_µ的导数定义(指标 µ 表示四维欧几里德时空指标，如µ = 1, 2, 3, 4)：

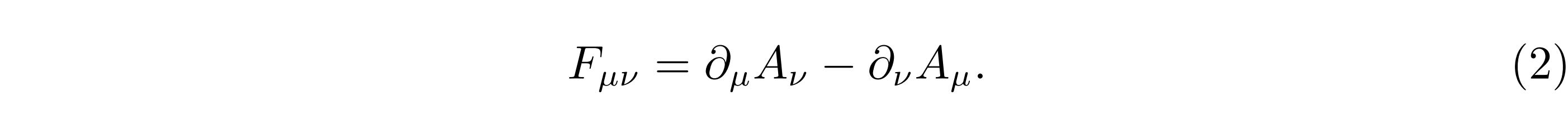
式 (1) 中的第二项则描述了自由电子(或一般费米子)场的相互作用能量，这里的ψ就是电子的狄拉克旋量波函数，ψ是其共轭场，γ^µ是狄拉克矩阵，m 是电子的质量。这一项源自于电子的狄拉克方程，狄拉克方程描写自旋为1/2费米子的相对论性量子行为。该项中的 D_µ 称为协变导数，它和普通导数 ∂_µ的关系是：D_µ = ∂_µ + i e A_µ(协变导数能够保持时空度规的规范不变性)。将协变导数带入第二项中，自然会得到一项−e ψ γ^µψ A_µ ，这一项直接描述了电子场ψ与电磁场A_µ的耦合相互作用，其耦合强度由基本电荷电量 e 决定，这一项在量子化后，能给出电子发射或吸收光子的费曼图的顶点，它成为所有电磁相互作用过程的起源。显然在经典的电磁学理论中，电磁场的来源是电荷，而电磁场和物质相互作用中要求电荷守恒，那么你很容易发现无论是电磁场的规范变换还是物质场的相位变换都会带来额外的“场”，所以这种变换下要求系统具有满足电荷守恒的U(1)规范不变。例如对电子场ψ(x)作局部 U(1) 的相位变换ψ(x) → e^iϕ(x)ψ(x)时，系统的拉格朗日量(能量)物理上应该保持不变。所以为了抵消规范变换带来的额外的电磁矢势的变化 A_µ → A_µ(x)−1/e ∂_µϕ(x)，必须引入一个规范场补偿由此带来的相互作用项，而这个被引入的规范场正是电磁场，其量子化的激发就是光子。显然电磁场隐藏在QED拉格朗日量的规范不变中，所以电磁场就被称为规范场。

正当描写电磁相互作用的QED理论大获成功的时候，粒子物理领域也正处于一个实验上不断发现新粒子的“黄金时代”，大量的新粒子(如π介子、K介子等)被相继发现，随着基本粒子数据的堆积，理解它们之间的相互作用和转化的理论却显得滞后、混乱和复杂。根据建立在阿贝尔U(1)规范理论上的QED理论，人们需要不断为这些新发现的粒子和相互作用在拉格朗日量 L 中引入新的项，以便用来整合新发现的强相互作用和弱相互作用的诸多粒子场，导致粒子物理领域的理论变得越来越复杂，似乎缺少一个统一、优美且带有前瞻性的理论框架。此时的杨振宁正在美国的普林斯顿研究院工作(杨先生1949年经恩里科·费米和爱德华·泰勒推荐进入普林斯顿高等研究院，并于1952年成为该院的终生研究员)，此时他已经是粒子物理领域前沿的青年专家，他对当时粒子物理领域非常复杂和修修补补的研究结果总感到不满意，他一直在思考一个核心问题是：随着新粒子越来越多，描述它们相互作用的运动方程会变得极其复杂，我们需要一个全新的基于对称性原理来归纳这些结果的方程，才能体现理论的统一性和简洁的美感。杨振宁提出杨-米尔斯理论的灵感来源于他早年在芝加哥大学攻读博士学位期间的一个不成功的尝试：能否将描述电磁力的外尔规范理论(基于 U(1)群)推广到更复杂的对称群上用以描述新发现的粒子和它们之间的相互作用。

1953到1954年期间，杨振宁到位于纽约长岛的布鲁克海文国家实验室(Brookhaven National Laboratory)进行学术访问。在那里，他与同在办公室的年轻物理学家罗伯特 · 米尔斯(Robert Mills) 就这个问题进行了深入的讨论。在与米尔斯的讨论中，米尔斯对这个想法产生了浓厚兴趣，他们的深入讨论使这个问题的方向越来越清晰，最终他们将规范场理论从U(1) 阿贝尔群推广到了SU(2)非阿贝尔群(同位旋群)，并在1954年共同发表了题为“同位旋守恒和广义规范不变性”的论文，正式提出了非阿贝尔规范场理论，即所谓的杨-米尔斯理论。显然杨-米尔斯理论遵从了QED中的逻辑思路，和U(1)规范群上的电荷守恒类似，强相互作用中的同位旋守恒要求同位旋在定域SU(2)对称变换下保持不变。为了维持这种对称性，就必须引入相应的规范场，即一种新的矢量场(后来被称为规范玻色子)，并给出了描述其性质的杨-米尔斯方程。起初杨-米尔斯理论的拉格朗日量只包含QED理论(1)的第一项(不包括物质场)，即规范玻色子矢量场：

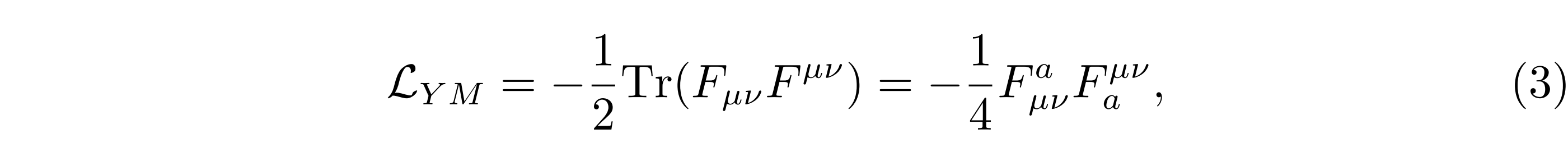
其中规范场强张量:F_µν = F_a ^µν L_a ，而L_a是规范场所属规范对称群(记为G)的生成元，它所对应的规范场强度张量F^a_µν由规范势 A^a_µ定义(a 是群指标，µ是四维时空指标)：

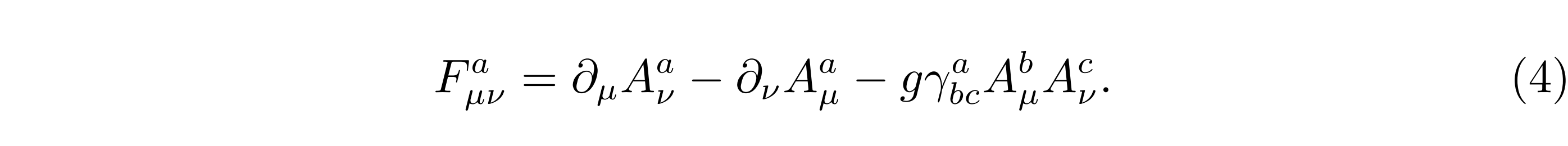
方程(4)中的非线性项−g γ^a_bc A^b_µ A^c_ν正是规范对称群 G 为非阿贝尔群的体现，它导致了规范场的自相互作用，其中 g 是耦合常数，γ^a_bc是规范对称群 G 的结构常数：

它代表了规范变换的非交换性或非线性的相互作用强度。(1)式中的F^µν是F_µν的对偶场，可定义为：

其中ϵ^µνση为四阶全反对称张量，可规定ϵ¹²³⁴ = 1，这和四维空间上的度规约定有关。如果规范对称群G的生成元{L_a , a = 1, 2, ··· , dimG}是有限的，它能构成一个有限维的李群，根据李群的表示理论，李群元素所给出的规范变换U(x)在一定的表象下可以写为：

其中求和指标a的上限dimG表示李群矩阵表示的维数，L_a为李群在该表示下的无穷小生成元，系数g称为耦合系数。

对于一般对称群G上的杨-米尔斯规范场，描述它的最基本的动力学量就是所谓的矢势A^a_µ  (vector potentials)，指标µ表示四维欧几里德时空指标µ = 1, 2, 3, 4，而群指标a对应于规范场的内部对称性，对应于一定的规范群表示。为描述时空物质场ψ(x)的协变性质，引入协变导数 (注意求和指标)：

显然对物质场函数ψ(x)进行式(5)所定义的规范变换：ψ′(x) = U(x)ψ(x)，那么协变导数 D_µ具有规范不变性：

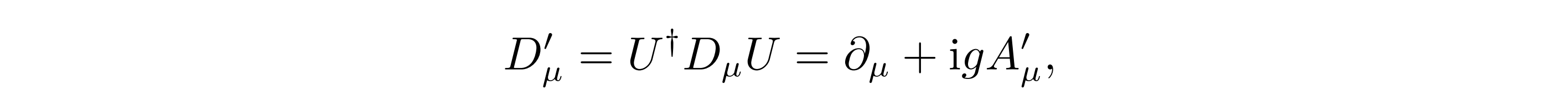
而其中的规范矢势 A_µ 显然不满足规范不变：

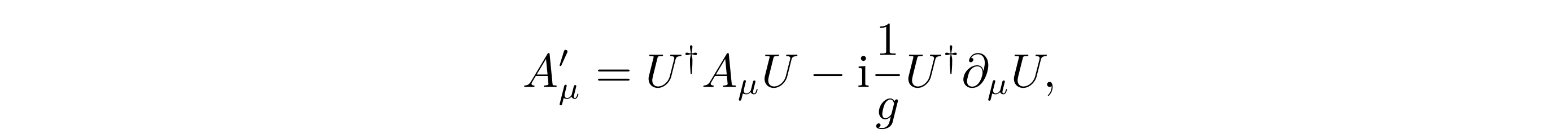
因为它多了一项，而这一项的出现就是规范场的来源。从几何角度来看，规范势A_µ对应于四维时空流形纤维丛上的联络(纤维空间是规范群所定义的矢量空间)，而场强 F_µν则对应其曲率。

利用杨-米尔斯的拉格朗日量(3)取如下规范不变的作用量：

利用传统的变分方法，利用作用量S_YM对规范场A^a_µ(x)求泛函变分：δS_YM = 0，即计算 δS_YM /δA^a_µ(x) = 0，给出如下的杨-米尔斯方程：

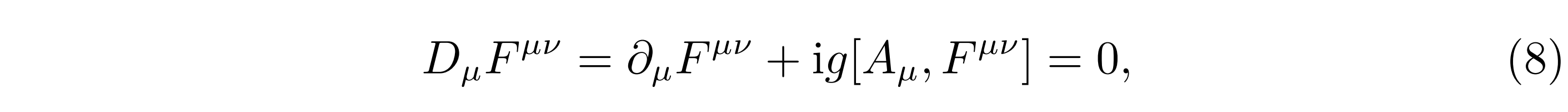
写成分量形式为：

其中 γ^c_ab就是前面提到的规范群 G 的结构常数。

显然如果规范群G = U(1)，群的生成元只有一个单位元(对应光玻色子)，杨-米尔斯理论就回到普通的电磁场理论；如果规范群G = SU(2)，对称群的生成元矩阵就是泡利矩阵(Pauli atrices)，有三个生成元(对应2² − 1 = 3个弱力玻色子)，这就是杨-米尔斯用来解释同位旋的规范场理论；如果规范群G = SU(3)，有八个生成元(对应3² −1 = 8个强子)，对称群生成元的矩阵就对应盖尔曼矩阵(Gell-Mann matrices)，这就是盖尔曼等人发展起来的量子色动力学(QCD: Quantum Chromodynamics)理论。

2. 标准模型的建立

起初杨-米尔斯理论在提出后的十多年内并未被科学界广泛重视和接受，因为该理论一开始就存在两个明显的缺陷。首先，杨-米尔斯理论要求强相互作用中的规范玻色子和光子一样没有质量，但这与实验中观察到的短程力(如核力)要求媒介粒子(如W± /Z玻色子)具有质量相矛盾，这个理论与实验的明显矛盾被称为杨-米尔斯理论的质量困难。其次，当时也无法证明：包含非阿贝尔规范场的杨-米尔斯理论是否能像QED理论一样可以被重整化而用来计算有限的物理量。然而沿着推广规范群的道路，杨-米尔斯规范场理论却显示了持续发展的强大生命力。

1961年初遵从杨-米尔斯理论的规范群思想，盖尔曼利用SU(3)群的对称性对强子进行了八分类(8个生成元)，基于此1964年盖尔曼提出了完整的夸克模型(1969年盖尔曼因对基本粒子的分类及其相互作用的研究发现而获得诺贝尔物理学奖)，之后在SU(3)规范场理论框架下逐渐发展出描述强相互作用的量子色动力学(QCD)，从而完善了标准模型的基本相互作用的理论框架。

1964年，弗朗索瓦·恩格勒、彼得·希格斯、罗伯特·布劳特(Robert Brout)等人在G = SU(2)×U(1) 群的基础上提出了著名的希格斯机制，通过引入复标量场(希格斯场)的自发对称性破缺，使规范玻色子获得了质量，同时又保持了体系的规范对称性(2008年的诺内尔物理学奖中南部阳一郎的工作是引入自发对称性破缺思想，为希格斯机制铺平了道路，而小林诚和益川敏英的工作则涉及弱相互作用可重整化理论中的CP对称性破缺问题)；之后希格斯机制所预言的上帝粒子：希格斯玻色子，2012年也在欧洲核子研究中心(CERN)的大型强子对撞机(LHC)上被发现，为标准模型补上了最后一块“拼图”(2013年恩格勒和希格斯二人也因此获得了诺贝尔物理学奖)。

1967-1968年，谢尔登·格拉肖、阿卜杜勒·萨拉姆和史蒂文·温伯格利用SU(2)×U(1)规范群上的杨-米尔斯理论，成功统一了电磁力与弱力，并预言W± , Z₀玻色子的存在。1973年中性流弱相互作用被发现，1983年W/Z玻色子也在CERN的LHC上被发现(1979年，这三位物理学家因对电弱统一理论的贡献，特别是对弱中性流的预言而获得诺贝尔物理学奖)。

1971-1972年间，杰拉德 · 特 · 胡夫特和马丁纽斯 · 韦尔特曼证明了非阿贝尔规范理论(包括希格斯机制)是可以重整化的，清除了该理论量子化过程中的数学障碍(1999 年二人因阐明物理学中电弱相互作用的量子结构而获奖)。

1973年，戴维 · 格罗斯、戴维 · 波利策、弗兰克 · 维尔切克发现强相互作用中的渐进自由现象，证明SU(3)规范理论(描述夸克间的色相互作用)在高能下耦合常数变小，低能下会发生色禁闭 (2004年三位物理学家因发现强相互作用中的渐近自由而获奖)。

至此沿着杨-米尔斯规范场的道路，在SU(3)×SU(2)×U(1)规范群的基础上标准模型的理论框架基本建立，所以标准模型(SM: Standard Model)就是粒子物理学中用来描述物质的基本组成及其相互作用(强力、弱力、电磁力)的基本理论框架。标准模型在物质结构的基本组成方面将宇宙中的基本粒子分为两大类：费米子(构成物质的粒子)和玻色子(传递作用力的粒子)；在相互作用方面，标准模型成功统一了除引力外的三种基本相互作用力：强相互作用(由胶子传递，将夸克束缚成质子、中子等强子)，弱相互作用(由W和Z玻色子传递，导致弱相互作用参与下的放射性衰变，包括所有涉及夸克味改变或轻子数改变的过程)，电磁相互作用(由光子传递，将原子、分子束缚成我们周围世界中各种各样的物质)。总之，以上所涉及的基本粒子及它们之间的三种相互作用力的数学描述都是基于外尔和杨-米尔斯理论所发展起来的规范场理论，其规范对称群建立于G = SU(3) × SU(2) × U(1)之上，因此，标准模型也被称为基本粒子的规范场理论。至此SM被誉为物理学发展史上又一个极为成功的科学理论，它基于量子场论并与量子力学和狭义相对论相容，主导了20世纪50年代以来的物理学的发展主线。

3. 标准模型数学和物理的局限

纵观物理学史，我们不难发现标准模型和其他成功的理论一样，代表着物理学发展史中一个阶段的成功总结，当然也并非是物理学的终极理论。很明显，标准模型本身包含着明显的局限和未解之谜。首先，从目前来看标准模型似乎只是一个微观理论，因为它并没有包含形成大尺度天体结构的万有引力(科学问题34引力的本质)，它能否在更大的规范群下去描写万有引力场目前并不清楚，但从物理突破的角度似乎存在一定的困难，所以标准模型需要进一步扩展(比如利用几何结构如纤维丛上的超对称规范场模型)，就如同当初成功的QED理论一样。其次，在目前的标准模型中假设中微子的质量为零，但1998年日本超级神冈实验发现了中微子振荡现象(2015年日本科学家梶田隆章和加拿大科学家阿瑟 · 麦克唐纳因此获诺贝尔物理学奖)，中微子振荡表明中微子应该具有微小质量，这就表明标准模型需要进行修正。同样在宏观方面，标准模型也无法解释宇宙中大尺度观测所预示的宇宙中大量存在的暗物质和暗能量，也无法解释为何宇宙中的物质远多于反物质(科学问题37中微子的反粒子)。作为一个基本粒子的基本模型，标准模型包含了至少大约19个非基本的自由参数(如包括10个粒子质量参数，4个相互作用参数，4 个夸克混合参数，1 个希格斯场真空强度，如果考虑中微子质量和转换混合参数至少也要引入 7 个参数)，而这些参数值需由实验确定和输入(它们是标准模型与实验数据拟合的基础)，而非由理论推导得出，这也表明标准模型并非是一个底层的基本理论模型。

这些问题的存在也表明建立在量子规范场理论基础之上的标准模型其数学基础恐怕依然没有到达底层坚实的地基，但杨-米尔斯规范场的思想，尤其在几何结构及对称性决定组成和相互作用的主线下，标准模型和宏观大尺度的万有引力也许会在诸如时空流形上的纤维丛、联络和曲率等等一些更一般概念所搭建的框架下获得统一，然而这仅仅是一种理论形式上的猜测，更深的地基依然隐藏在数学和物理的大厦之下更深的地方。面对标准模型所存在的问题科学家们其实并没有停止探索的脚步，所以在标准模型之外人们已经进行了多种尝试(比如影响力很大的弦和超弦理论)，然而目前来看物理学的发展历史似乎又进入到了QED理论成功之后的那个时期，各种大统一理论(科学问题5物理定律的统一)并存却在缺少更多实验数据的情况下越来越抽象和模糊，对普通大众来说这些缺乏物理真实数据支撑的理论似乎正越来越走向神学或玄学的方向，然而这些看似抽象的理论对数学的推动和对科学的促进总有一天会把物理学从迷雾中推向光明的新大陆。