平均可支配收入、平均家庭财富、平均身高、平均成绩……我们处处都能看到平均值的身影，平均值毫无疑问是我们用的最频繁的统计量！一种很自然的错觉就是掌握了一个群体的平均值，似乎也增强了我们对这个群体中个体的认识。这个错觉也恰恰成为平均值之所以流行的原因——还有什么比只看一个数值就能了解情况更好的办法呢？

白色的太阳光经过折射和反射之后，变成了七色的彩虹；反过来我们也可以说，彩虹的“平均颜色”是白色的。这个隐喻告诉我们，随随便便取平均，很可能让斑斓坠入黯淡。

在中国，衡量居民收入水平最常用的指标是可支配收入，它是指居民可用于最终消费支出和储蓄的总和，包括工资性收入、经营性收入、财产性收入和转移性净收入四个部分，其中转移性净收入等于常态转移性收入（如退休金、政策性生活补贴等）减去常态转移性支持（如房贷），有可能是负值。可支配收入较好地反映了居民的生活和消费水平，是分析我国宏观经济趋势的核心指标之一。我们见到的最多的数字叫做“全国居民人均可支配收入”，这个数字远远低于人均工资，因为后者的分母只包含全职工作者，而前者要把没有收入的小孩子和收入较少的老年人以及无固定职业者都纳入计算中。根据国家统计局2023年1月17日的公开报告，2022年全国居民人均可支配收入36883元。那么，我们要怎么理解这个“平均值”呢，是不是意味着一半左右的人收入在36883元之上，一半左右的人收入在36883元之下？这可能是我们的第一感觉，但遗憾的是，这和真实的情况相差很大。实际上，2022年全国居民可支配收入的中位数仅为31370元，仅为平均数的85%。也就是说，真实的情况是，有一半的居民收入在31370元以上，另外一半的居民收入在31370元以下。

造成平均数和中位数有显著差异的原因是分布向右倾斜，也就是和具有相同平均数和方差的正态分布相比，真实的分布有更多的“大值”出现。正是这些“大值”，例如年可支配收入在1000万以上的富豪们，拉高了平均数。在这种情况下，平均数就无法真实反映我们直观中的“平均情况”，而中位数是一个更好反应居民平均情况的指标。显然，分布向右倾斜得越厉害，平均数就更受“大值”个体的影响，从而距离我们直观中的平均更远。举个例子，初次分配收入要比可支配收入额度分布更加右斜，因为初次分配收入高的人缴纳的税负比例更高，所以通过不同比例的转移支付，可支配收入的差异要明显小于初次分配收入的差异。如图1所示，收入分布的平均数和中位数差异更大.从全球范畴来看，2003年收入的中位数仅为平均数的31.59%，2013年这个数字增长到了37.40%，预测中的2035年，这个比例有望提高到43.90%，依然不到50%。一般而言，平均数和中位数相差越小，说明分布中的“大值”越少，贫富差异往往也比较小，对应更小的基尼系数。正因为平均数和中位数有很大差异，当平均工资公布的时候，我们总会觉得自己拉了所在城市的后腿——实际上大部分人的收入都会小于平均收入。如果你所在城市的平均年收入是100000元，而你一年的收入只有80000元，那么恭喜了，你实际上已经战胜了一半的同城者。

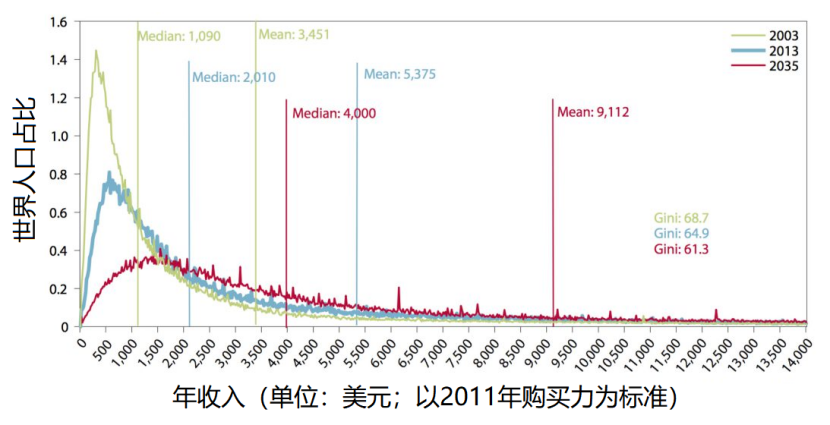
图1：2003和2013年全球年收入分布以及世界银行预测的2035年全球年收入分布。

如果说平均数和中位数差不多（这种情况往往分布大致上是中心对称的），那么平均数是否就能很好地刻画个体的情况？其实也不一定。如果标准差相比平均值而言是比较小的，那么参考价值就很大了。比如中国成年男性平均身高在175厘米左右，而标准差在6厘米左右，那么这个175厘米就很有参考价值了，因为身高分布是典型的正态分布，而身高在3个标准差之外占比仅有0.3%，意味着一千个成年男性中，仅有三名左右身高低于157厘米或身高高于193厘米。但是如果分布非常宽广，即便是中心对称的，平均数等于中位数，这个平均数的参考价值也不大。比如说，一条水深大致上呈现中心对称的河，两岸水非常浅，河中心水深却可以达到三米，整条河水深的平均值大约是1米，那么知道这条河平均水深1米，对你做决策（能不能趟水过河）有帮助吗？我觉得几乎没有。

Silver曾经讲过一个恶毒的段子[1]：“一位统计学家趟过一条平均水位不足1米的河时，竟被淹死了。”我建议各位读者以后在碰到平均数的时候，先在脑海里默默念一遍这个段子。

参考文献：

[1] 纳特·西尔弗，（胡晓姣、张新、朱辰辰译），《信号与噪音》，中信出版社，2013。