博文
大自然中的蒙特卡罗模拟(一)
 精选
精选
|||
第一节:随机行走(以二维做为为例子)
大自然中许多运动过程都是随机的,最为我们所熟知的是布朗运动,小的花粉颗粒在水中,由于受到了随机的作用力而在水中进行着随机行走,除此之外,随风飘零的落叶,蚂蚁在找寻食物,动荡的股票,甚至醉酒的路人的走路等等都是随机过程。
图1:醉酒者进行随机行走[1]
大自然中充满了那么多的随机运动,为了了解它们更加深刻的美丽,我们需要学习如何研究它们,其中一个办法便是蒙特卡罗模拟。蒙特卡罗模拟是先对研究对象进行仔细的分析,然后产生一系列随机数,并建立所需要研究问题的模型,进行多次随机实验,让我们需要了解的物理量是模型中的某些量的平均值或者和这个平均值有关的量,进行分析和计算。
回到随机行走的话题,关于随机行走,可以分为三类,第一类是简单的随机行走(random walk),假如有一个灰尘粒子,在空气中做随机行走,不考虑重力的影响,灰尘向各个方向运动的几率都是一样的,如在二维空间中,粒子有四种选择,即上下左右,每个方向的概率都是0.25,此时我们关注的物理量如<r^2>(r是n个步长之间的距离)就可以利用计算模拟得到<r^2>~x1,x为n个步长。结果如图2,图3所示:
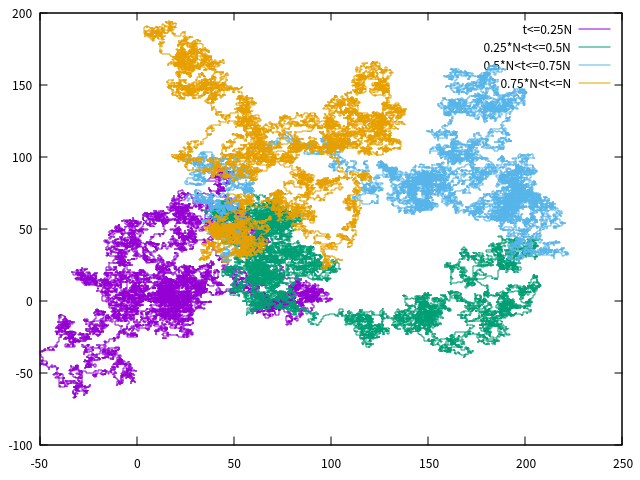
图2:简单抽样的随机行走,不同的颜色代表不同的时间段粒子的行走路线。

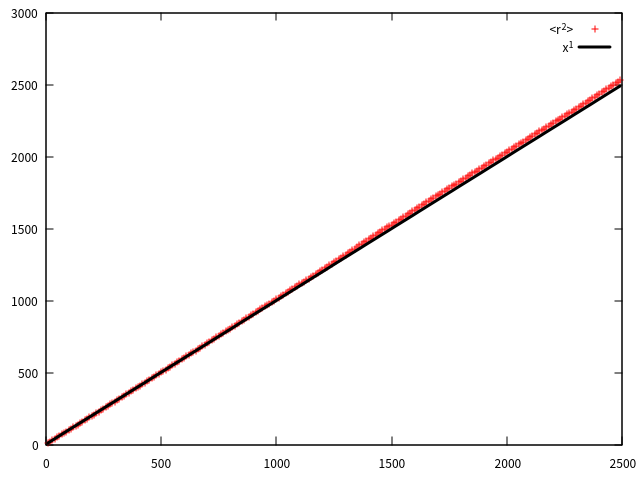
图3:(上)简单的随机行走的x,y随着时间的变化的结果;(下)n个步长的距离与n个步长之间的关系
当粒子变得更聪明了,即有了简单的记忆之后,就可以变成更加复杂一点的随机行走,例如人走路,每一步会时而左,时而右,总体方向朝前,几乎不会原地连身体都不转一下就朝后行走(除非有目的的朝后走),又例如,一款经典的小游戏—贪吃蛇中,蛇可以向前,向上,向下行走,但是,它不能直接向后,即此时随机行走有了一定的记忆性,它记住前一步的位置并避免朝回走(non-reversal random walk)。这种随机行走在模拟中有两种不同的方法,第一种是在粒子做选择的时候,依然朝四个方向的几率相同,当选择到了前一步的位置的时候,则进行重新选择,直到朝其他方向走去为止,此时每进行一次选择,都需要判断是否是前一个位置,如果是重选,如果否,则新的位置变成了前一步,继续往前做新的判断和选择;第二种办法就是记住前一步的具体位置,直接排除这个位置,只在三个方向中进行选择,每走一步,把该位置记住,下一次直接排除它。两种办法虽略有不同,但是结果是相同的即反映出来的规律是一样的,如图4,图5所示:
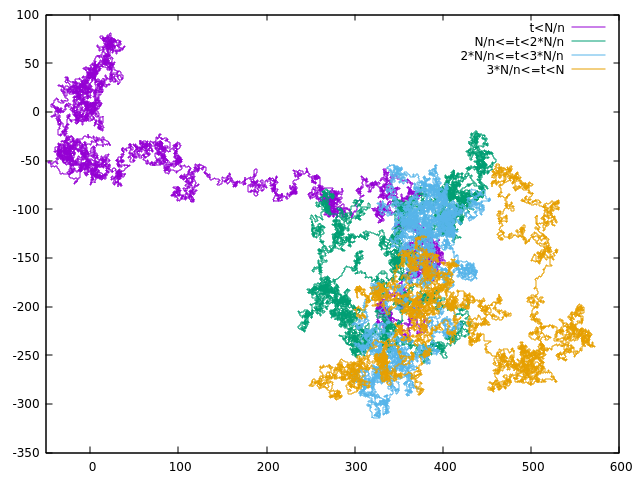

图4:两种不同的方法的不返回随机行走。上边是第一种办法即每次四种选择,若选择了前一步的位置则重新选择,下边的是第二种方法即先记住上一步的位置每次做选择只有三种可能。
图5:不同的方法得到的不原地折返的随机行走的<r^2>,<x^2>,<y^2>的规律
图4两张图只能反映粒子的轨迹,看上去似乎两种方法结果不同,但是这仅仅是表面看到的结果,实际上从图5可以看到,实际上两种方法得到的结果是相同的。
那么进一步,当粒子不仅仅能够记住之前的一步的位置,而是此时,粒子的记忆力增强了,它记住了自己走过的所有地方,由于一种特殊的爱好,这个粒子只喜欢新鲜的没有走过的位置,即每次粒子都不能够再走那些它走过的地方。此时称之为自回避随机行走(self-avoiding random walk),这个时候,粒子变得挑剔,也正是因为这样,往往会把自己陷入死胡同,因而,如果用简单的抽样办法,粒子的行走很快就会因为自己的特殊爱好而终结即无路可走了,如图6所示,如何解决这个问题呢?这将在下次介绍。

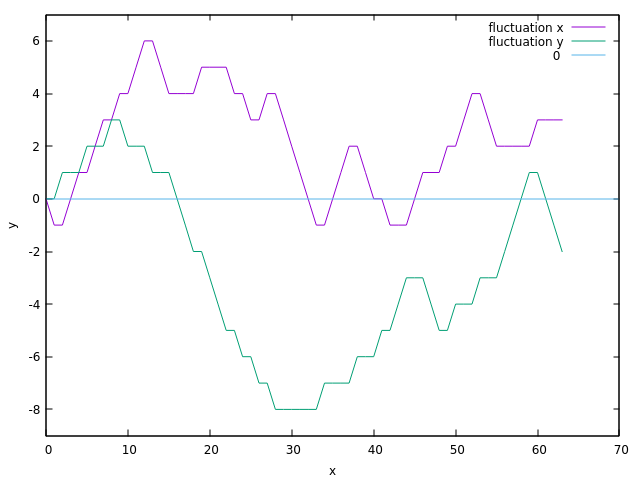
图6:自回避随机行走的结果,粒子从(0,0)点出发,经过六十多步之后,行走便终止了。
第二节:DLA模型与大自然中的奥妙
当了解了随机行走,我们会发现还有很多其他现象与之有关,例如一个著名的随机模型:DLA(Diffusion Limited Aggregation)模型。该模型最早是用来解释粉尘的沉积与静电击穿中产生的美丽花纹的。它让我们感受到了那些深层的美丽,即使这个模型本身并未加入过多的物理因素,但也正因如此,它得以在许多不同学科中被运用。
假如我们有一个粒子,把它当作一个核(也称为种子),而在离核有一段距离的地方(选在某个圆环上的某处)产生一个粒子,让粒子进行随机行走,如果粒子走出了圆环,则将其抛弃,如果粒子接触到了中间的核,则加入它称为它的一部分,然后再产生一个新的粒子,进行重复以上过程。当产生了足够多的粒子之后,美丽的花纹便出现了。
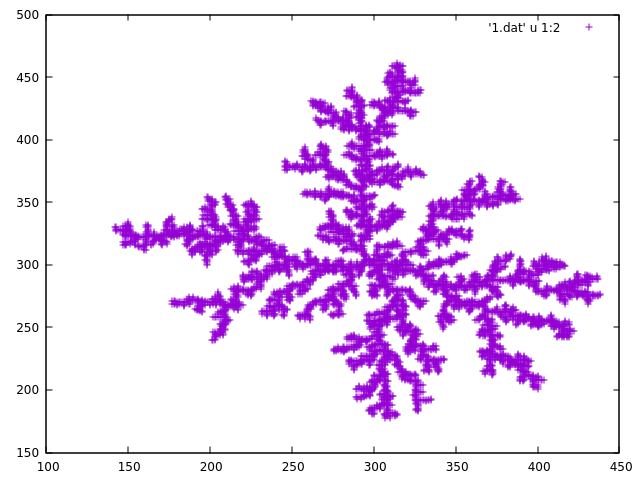
图7:DLA模型中粒子聚集产生的花纹
如果它仅仅只是美丽的,那事情就该结束于此了,毕竟,许多人用计算机可以绘画出许多惊人的图片,然而,DLA模型的结果与大自然中或者实验室中的许多现象如细胞的凝聚生长,化学中的凝聚,物理中的静电击穿等等惊人的相似,并且它们的过程也很像,DLA模型为我们研究其他现象提供了计算模拟的办法,此时不得不提及该花纹与分形的联系,这个美丽的花纹和许多分形的图案一样,是分形的,可以计算分形位维数,有兴趣的可以去进一步了解。

图8:实验中的观察到的DLA花纹。
第三节:玻璃上的冰花,落在上面的雪与冰在水中的生长


图9:(上)落在车窗上的雪;(下)玻璃上的冰花[2]。
图10:冰在水中的生长。
大自然总是充满了美好与神秘,如玻璃上的冰花,落在车窗上面的雪与冰在水中的生长,它们是如此的美丽,而从某种角度来看,它们又可以看作是一种随机过程,以雪花落在竖直的车窗为例,雪花在空中飞舞,由于重力的作用,雪花朝下的几率比较大,但是风带来的扰动让雪花依然可以朝左右甚至向上运动,而风是随机的,因而落在窗户上的位置因该也是随机的,但是长时过后,许多雪花晶体的飘落在车窗,竟然呈现出的是一种有规律并非完全覆盖车窗的结果,似浪潮又似网格式的排列,实在太美!
为了模拟类似的景象,假如考虑二维的情况,让一个粒子在二维网格的中间出发进行随机行走,当粒子接触两边的边界或者接触到其他粒子的时候,粒子停止不动,加入其他粒子或者自己变成了一个新的核,得到了图11的结果。

图11: 粒子在中间开始随机行走
大自然总是充满了各种奥秘,如果你想去发现它,那就停下脚步,去细细品味其中的美与乐趣吧!
Reference:
[1] James P. Sethna,Statistical Mechanics:Entropy, Order Parameters, andComplexity,Oxford University Press,2006.
[2] http://all-free-download.com/free-photos/download/ice-flowers-glass-window_274167.html
[3] K.Binder,D.W.Heermann, Monte Carlo Simulation in Statistical Physics(5th),Springer, 2006.
最后,有几张生活中的小图片与大家分享:




https://blog.sciencenet.cn/blog-739225-1033478.html
上一篇:冰冻滴落的液珠
下一篇:球面上的布朗运动
全部作者的精选博文
- • 球面上的布朗运动2--更简单的模拟方法
- • 主动布朗粒子
- • 球面上的布朗运动
- • 冰冻滴落的液珠
- • 液珠击打在细纤维等物体上
全部作者的其他最新博文
- • 终于毕业了-荷兰的生活
- • 球面上的布朗运动2--更简单的模拟方法
- • 主动布朗粒子
- • 球面上的布朗运动
全部精选博文导读
相关博文
- • AAA PCI -- 学者心声(Authorea 预印论文报道)
- • Building a DIKWP-TRIZ Software System (初学者版)
- • DIKWP-TRIZ: Semantic Blockchain and Semantic Communica(初学者版)
- • DIKWP-TRIZ in 3-No Problem and Artificial Consciousnes(初学者版)
- • Comparison Between DIKWP-TRIZ and TRIZ(初学者版)
- • DIKWP-TRIZ: Enpower AI/AC Innovation (初学者版)