博文
反应渗透网络结构控制
||
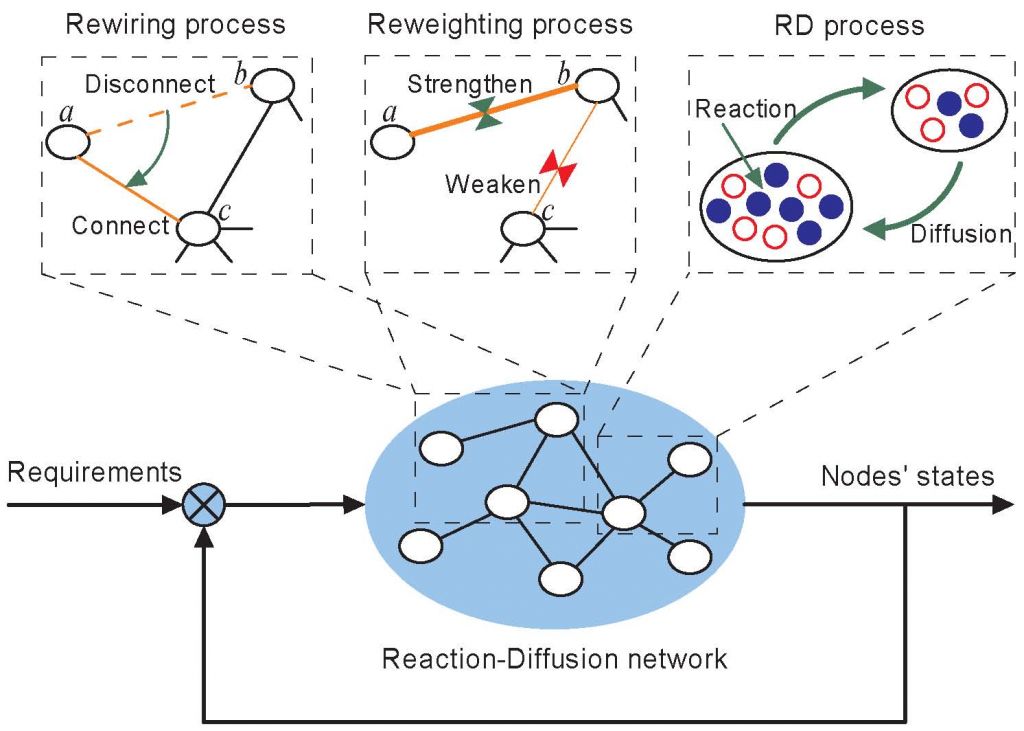
反应渗透过程(RD Process)包括两个简单的过程:粒子在空间的渗透以及不同粒子随机碰撞发生反应,由于其能够从微观角度解释许多物理现象,包括化学反应,生物体斑纹形成,疾病传播等等,因此深受物理学家喜爱。随着复杂网络理论的展开,传统的离散欧氏空间(网格)被扩展到一般化的网络空间,因此,近些年有些物理学家开始研究复杂网络上的渗透反应过程(包括经典的SIS模型),发现其结果和在传统网格上的结果有显著差异[1,2,3]。既然结构能影响动力学,那我们能不能通过控制网络结构来一定程度地控制其上的动力学行为呢?答案是肯定的,鉴于此,我们提出了反应渗透网络结构控制的概念,其基本框架如图一所示。
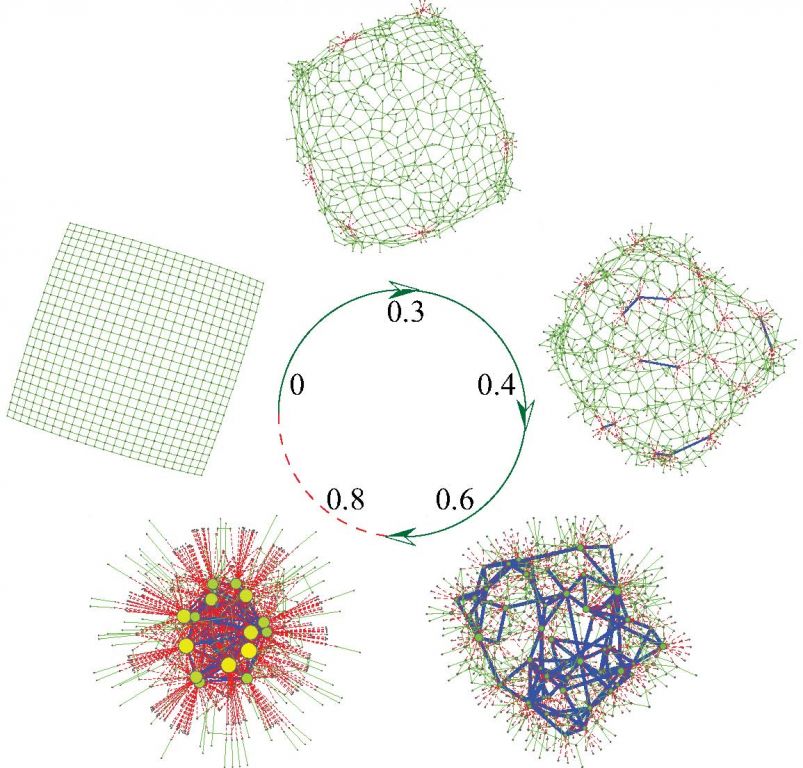
举个例子:假设每个节点是一个智能体,它能感知自身状态和周围环境之间的差异,与此同时,它还能进行随机连边操作来达到消除此差异的目的,最终在节点这种“自私自利”的本性以及完全随机的操作下,网络结构是否能够达到稳定?即所有节点的状态都达到外部需求,不再寻求改变?答案是肯定的,我们以SIS模型为例,其中包含两种粒子,记为alpha和beta,它们之间通过反应式beta->alpha和alpha+beta->2beta互相转换,与此同时,它们在网络相邻节点间互相渗透。假设外部需求为鼓励beta粒子,即对每个节点设为rho_{beta,i}/rho_{i}>theta ,对于此模型以及此外部条件,利用反应渗透网络结构控制机制,可以得到网络的演化过程(对应于不同的参数theta)以及控制效果图分别如图二和图三所示。
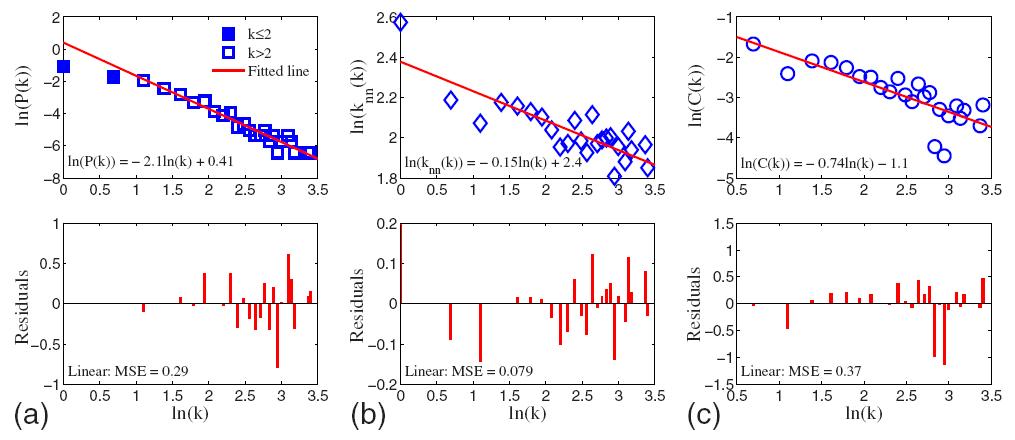
值得注意的是,当theta取值过大,网络有可能失稳,此时我们认为系统不可控,比如在我们这个例子中,当theta>0.6时,网络就会失稳。因此分析theta=0.6时的网络结构就会比较有价值,图四给出了theta=0.6时网络的度值分布,度相关函数,以及聚类函数,与许多现实复杂网络的特征比较吻合(由于蒙特卡洛方法比较耗时,所以网络规模不是很大,最终的统计结果就会有些出入)。由于生物体内存在大量的纳米级别的反应渗透过程[4],如图五所示,同时温度压强等都有严格的限制,因此结构控制很有可能作为其中的主要控制手段来控制在不同的阶段生成不同比例的反应产物,故本研究在了解生物体内部异质网络结构的形成或许具体一定的价值,更多内容请参考我们的文章[5,6]。
再过一个月第七届复杂网络会议就要在成电举行了,很期待,希望能在涛兄的实验室学到点东西,哈哈,也提前把自己初步的PPT贴一下吧(渗透反应网络结构控制.ppt),希望和广大志同道合的朋友们讨论切磋下。另外网络数据挖掘还是本人主业,有兴趣的兄弟到时候一起探讨,留个MSN email:crestxq@hotmail.com,随时联系。
参考文献:
[1] L. K. Gallos and P. Argyrakis, Absence of kinetic effects in reaction-diffusion processes in scale-free networks. Physical Review Letters, 92(13): 138301, 2004.
[2] V. Colizza, R. Pastor-Satorras, and A. Vespignani, Reaction–diffusion processes and metapopulation models in heterogeneous networks. Nature Physics, 3: 276-282, 2007.
[3] V. Colizza and A. Vespignani,Invasion threshold in heterogeneous metapopulation networks. Physical Review Letters, 99(14): 148701, 2007.
[4] L. Lizana, Z. Konkoli, B. Bauer, A. Jesorka, and O. Orwar, Controlling Chemistry by Geometry in Nanoscale Systems. Annual Review of Physical Chemistry, 60: 449-468, 2009.
[5] Qi Xuan, Fang Du, Tie-Jun Wu, and Guanrong Chen, Emergence of heterogeneous structures in chemical reaction-diffusion networks. Physical Review E, 82(4): 046116, 2010.
[6] Qi Xuan, Fang Du, Hui Dong, Li Yu, and Guanrong Chen, Structural control of reaction-diffusion networks. Physical Review E, 84(3): 036101, 2011.https://blog.sciencenet.cn/blog-307011-490911.html
上一篇:蛋白质关联网络到底干什么用的?
下一篇:浙工大信息学院诚聘复杂网络方向优秀博士生!