博文
无穷维空间上的一个泛函
|||
设 $X$ 是赋范线性空间, $\varphi:X\rightarrow R^1$ 是连续泛函,对单位球面 $S=\{u\in X|\|u\|=1\}}$ 上的每个元素 $u$ , $\varphi$ 都满足 。 问该泛函是否强制?亦即,能否推出 $\lim_{\|u\|\rightarrow \infty}\varphi (u)=+\infty?$
在有限维空间,利用球面的紧性不难证明,答案是肯定的。但对于无穷维空间,则不一定。我们在空间 $l^2$ 上构造一个例子。
定义一列实函数 $\{\psi_n\}$ 如下:
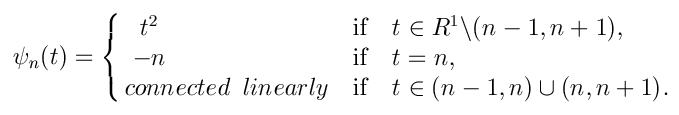
在空间 $l^2$ 上定义泛函 $\varphi$ 为:对 $u=(\xi_1,\xi_2,\cdots \xi_n,\cdots )$ $\in l^2$ ,
$\varphi (u)=\sum_{n=1}^{\infty}\psi_n(\xi_n),$
则 $\varphi$ 有意义且连续。对单位球面上的每个元素对 $u=(\xi_1,\xi_2,\cdots \xi_n,\cdots )$ ,设 $\xi_j\neq 0$ ,则
$\lim_{\lambda \rightarrow +\infty}\varphi (\lambda u)\geqslant \lim_{\lambda \rightarrow +\infty}\lambda^2\xi_j^2=+\infty.$
在 $l^2$ 中取一列元素 $\{u_n\}$ 如下:
$u_1=(1,0,\cdots ,0,\cdots )$ ,
$u_2=(0,2,\cdots ,0,\cdots )$ ,
$\vdots$
$u_n=(0,\cdots ,0,n,0\cdots )$ ,
$\vdots$
显然, $\|u_n\|\rightarrow +\infty,$ 而 $\varphi(u_n)=-n\rightarrow -\infty$ 。所以, $\varphi$ 与强制泛函相去甚远。
看到很多正规发表的论文,甚至SCI论文,也在这个问题上犯错误,实在不应该。
https://blog.sciencenet.cn/blog-112841-682544.html
上一篇:南京宏觉寺
下一篇:秦桧书法
全部作者的精选博文
- • 听老外讲汉语
- • 学数学,真的可以成为一种乐趣
全部作者的其他最新博文
- • [转载]杨振宁先生的数学贡献
- • 三星堆vs金字塔
- • 年过完了
- • 闲说教师节(旧文新发)
- • 秋游
- • 此词一出,余词尽废