博文
[转载] 割线法的动画图
||

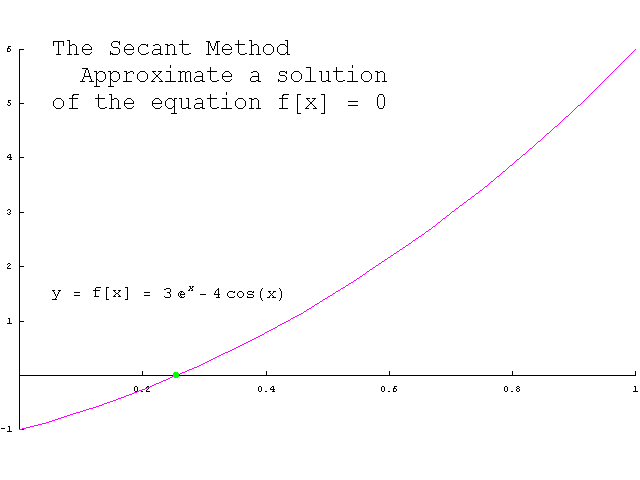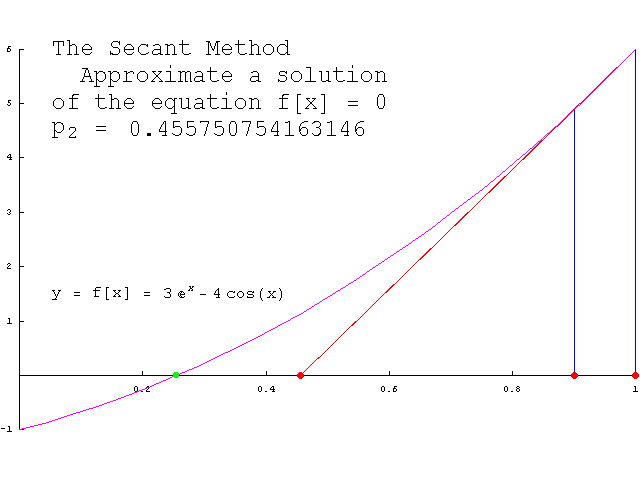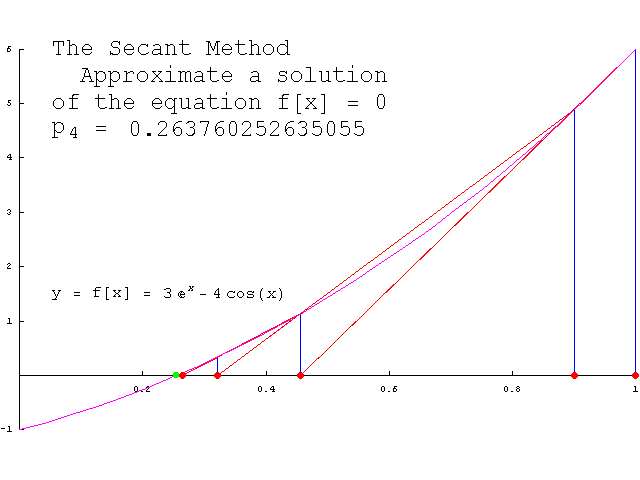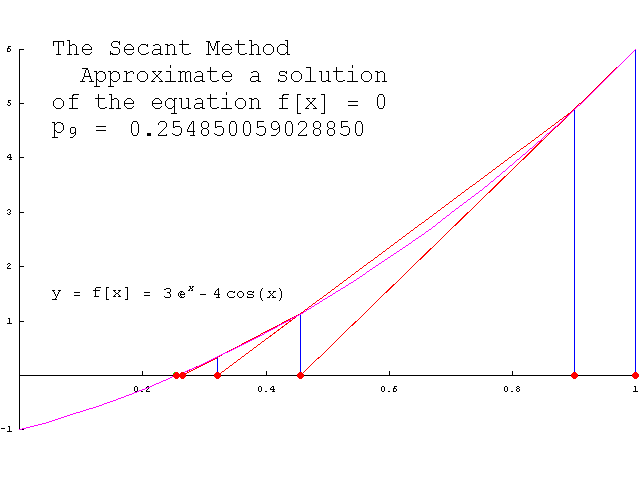




"割线法是一个求根算法,该方法用一系列割线的根来近似代替函数f的根。割线法比牛顿法 [又称为牛顿-拉弗森方法,方法使用函数

 。" -- https://zh.wikipedia.org/wiki/割线法 https://en.wikipedia.org/wiki/Secant_method:
。" -- https://zh.wikipedia.org/wiki/割线法 https://en.wikipedia.org/wiki/Secant_method:
"
割线法由以下的递推关系定义:
从上式中可以看出,割线法需要两个初始值x0和x1,它们离函数的根越近越好。
(The secant method is defined by the recurrence relation
As can be seen from the recurrence relation, the secant method requires two initial values, x0 and x1, which should ideally be chosen to lie close to the root.)
给定xn−1和xn,我们作通过点(xn−1, f(xn−1))和(xn, f(xn))的直线。注意这条直线是函数f的割线,或弦。这条割线的点斜式直线方程为:
我们现在选择xn+1为这条割线的根,因此xn+1满足以下的方程:
解这个方程,便可以得出割线法的递推关系。
(Starting with initial values x0 and x1, we construct a line through the points (x0, f(x0)) and (x1, f(x1)), as shown in the picture above. In slope–intercept form, the equation of this line is
The root of this linear function, that is the value of x such that y = 0 is
We then use this new value of x as x2 and repeat the process, using x1 and x2 instead of x0 and x1. We continue this process, solving for x3, x4, etc., until we reach a sufficiently high level of precision (a sufficiently small difference between xn and xn−1):
)
如果初始值x0和x1离根足够近,则割线法的第n次迭代x收敛于f的一个根。收敛速率为α,其中:
是黄金比。特别地,收敛速率是超线性的。
这个结果只在某些条件下才成立,例如f是连续的二阶可导函数,且函数的根不是重根。
如果初始值离根太远,则不能保证割线法收敛。
(The iterates 



is the golden ratio. In particular, the convergence is superlinear, but not quite quadratic.
This result only holds under some technical conditions, namely that 
If the initial values are not close enough to the root, then there is no guarantee that the secant method converges. There is no general definition of "close enough", but the criterion has to do with how "wiggly" the function is on the interval ![[x_{0},x_{1}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec10faf54bec6a09b997bebef2b4417ec2ebc8b0)


"
References
https://web.archive.org/web/20081017171843/http://math.fullerton.edu/mathews/a2001/Animations/RootFinding/SecantMethod/Secantaa.html
https://web.archive.org/web/20081017171848/http://math.fullerton.edu/mathews/a2001/Animations/RootFinding/SecantMethod/Secantbb.html
https://web.archive.org/web/20081017170102/http://math.fullerton.edu/mathews/a2001/Animations/RootFinding/SecantMethod/Secantcc.html
https://web.archive.org/web/20081017171853/http://math.fullerton.edu/mathews/a2001/Animations/RootFinding/SecantMethod/Secantdd.html
https://web.archive.org/web/20081026042452/http://math.fullerton.edu/mathews/a2001/Animations/RootFinding/SecantMethod/Secantee.html
https://web.archive.org/web/20081026051330/http://math.fullerton.edu/mathews/a2001/Animations/RootFinding/SecantMethod/Secantff.html
https://blog.sciencenet.cn/blog-498408-1200576.html
上一篇:[转载] Hadamard矩阵
下一篇:[转载]<<Molecular Structures and Structural Dynamics of PrP>>9月书评







