博文
第五章(四)Formally Refuting the Maksić’s Comment (全文)
|
Chapter 5: The Restricted geometry Optimization -
New Procedure to Get New Insight into Aromaticity
(这是投JPCA的正式批驳Maksić’s comment 的文章. 在批驳的同时,
我们严厉地批评了由在美国的华人副教授XXX与Schleyer 合作发展的BLW法)
Formally Refuting the Comment on “Restricted Geometry Optimization: A Different Way to Estimate Stabilization Energies for Aromatic Molecules of Various Types
Zhong-Heng Yu
Beijing National Laboratory for Molecular Sciences (BNLMS), State Key Laboratory for Structural Chemistry of Unstable & Stable Species, Institute of Chemistry, Chinese Academy of Sciences, Beijing 100190, People’s Republic of China
Abstracts: In the Maksić’s comment paper, there is almost no reference cited, and there is no his calculated data. The comments, completely being out of his personal feeling, are all incorrect. In the second year after the publication of the Maksić’s comment, our new paper was published on the Journal of Computational Chemistry, and it confirmed that our program is reasonable and calculates reliable extra stabilizing energy of benzene via the comparisons between our program, Morokuma’s energy decomposition analysis and the block-localized wave function (BLW) method.
1. Introduction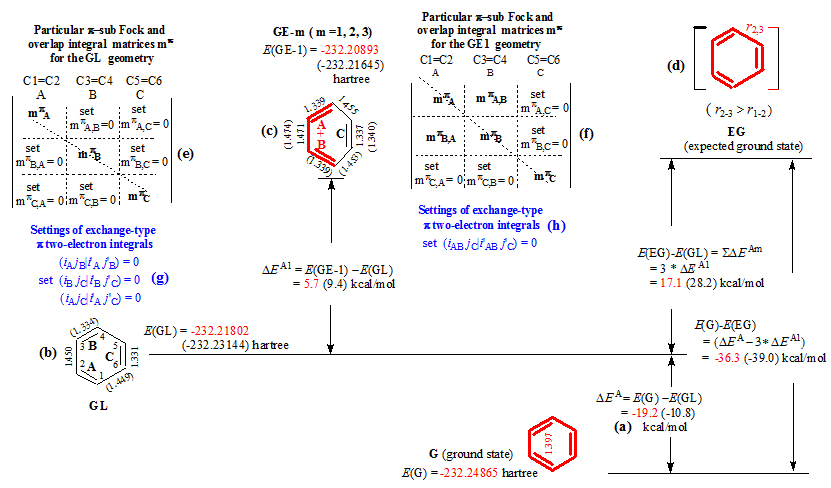
Figure 1. Procedure (our 2010 program) for calculating ESE of benzene, and definitions of the energy differences DEA and DEAm; (a), (b) and (c) The G (ground state), GL (geometry having localized double bonds) and GE-m (the mth particular) geometries were obtained from the full and restricted geometry optimizations at the B3LYP/6-31G* level, where the bond lengths are in angstroms, and their molecular energies, denoted as E(G), E(GL) and E(GE-m), are in hartree; (e), (f), (g) and (h) are the conditional settings for restricted geometry optimization of the GL and GE-1 geometries. For a specific geometry, the thick and thin lines indicate that all the p orbital interactions between the double bonds have been set to zero, except for those between the double bonds (thick line). The data in parentheses were calculated by our 2007 program in which the spatial exchange-type p two electron integral (ipjq½i'pj'q) (p ¹ q) are not set to zero.
Due to that the procedures, reported in literature, are insufficient to evaluate aromatic stabilization energy,[1] a program for restrictedly optimizing geometry (shortened to “restricted geometry optimization”, or “our 2007 program”) was developed in our research group,[2] and it provided a conjugated molecule with two types of localized reference geometries: (i) a GL (a geometry with the localized double bonds) geometry (Figures 1b), where the pi systems are absolutely localized on their respective double bonds, and (ii) the GE-m geometries (m = 1, 2, ……k) (Figures 1c). In each of the GE-m (mth particular geometry) geometries, only a specific pair of double bonds is permitted to conjugate; all other double bonds remain localized.
2. The Comment by Maksić.
The energy difference [E(GE-m) – E(GL)], reported in our 2007 JPCA paper, is always destabilizing, which, maybe, irritated Prof. Maksić. On December 24, 2008, the Maksić published his comment paper,[4] and he concluded that our 2007 JPCA paper is meaningless. In the original version of his comment manuscript,[5] however, there was nothing, almost no reference cited and no his calculated data, except for sarcastic and rude remarks, indicating that Maksić is not professional enough to be able to comment on the method for partitioning energy.
In our response,[6] on the contrary, 78 important references, as well as the original words of the famous researchers, were cited, which, together with our new calculation results presented in Supporting Information, reasonably refuted all Maksić’s criticisms. However, our response manuscript was rejected without question on Oct 27, 2008.
3. Our Newly Published paper.
3.1. Our 2010 Program. According to the study of Morokuma[7] and Bader,[8] the Pauli exclusion principle also controls spatial delocalization of electrons via the electron exchange (hereafter, called spatial exchange interaction) besides the orbital charge-transfer and exchange interactions among the isolated groups (double bonds). Accordingly, the electron localization should be conceptually different from molecular orbital localization.
In our 2007 program, therefore, deleting particular Fock matrix elements can only ensure that the orbital exchange and charge-transfer interactions among the isolated double bonds were excluded from a localized geometry. In addition, due to the full retention of all the two-electron integrals over the AO (Atomic orbital) basis set, deleting particular Fock matrix elements can’t guarantee that the contributions to the second-order perturbation correction energy all satisfy the principle of differential overlap. At the RHF (Restrict Hartree-Fock) and MP2 (Møller-Plesset perturbation theory) levels of theory, as a result, the size of the basis set has a great effect on the value of the ESE of benzene (Table 1), and the RHF and MP2 values of the ESE for benzene are much greater than the corresponding B3LYP values, leading to limitations in the use of our 2007 program.
Table 1. The values of the ESE for benzene were calculatedby our 2007 program (energy unit in kcal/mol).
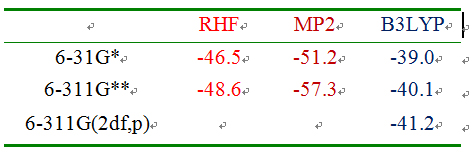
In order to improve our 2007 program and to formally refute the Maksic's criticisms, we published our 2010 program on the Journal of Computational Chemistry.[9] In each of the GL and GE-m geometries obtained from our 2010 program, all the interactions, including the orbital exchange and charge-transfer interactions and the spatial exchange interactions, among the localized double bonds, have been excluded. As a result, the B3LYP/6-31G* value of the ESE for benzene was changed from -39.0 kcal/mol (2007 program) to -36.3 kcal/mol (2010 program). -36.3 kcal/mol can be considered equal to the experiment value (36.0 kcal/mol). Particularly, as shown by the data listed in Table 2, the levels of DFT (Density Functional Theory), RHF and Post-SCF (post-Self-consistent-Field, MP2, CISD, CCSD) and the basis sets have slight effect on the ESE, meaning that DFT, RHF and post-SCF methods all become available for evaluating the ESE of aromatic molecule.
It should be emphasized that the energy difference, DEAm = [E(GE-m) – E(GL)], is always destabilizing (Figure 1) whether it was obtained from our 2007 or from 2010 program. In the case of the BLW (block-localized wave function) method, on the contrary, the energy effect, associated with pi-delocalization, is stabilizing. Therefore, it is necessary to compare our program with the BLW method to confirm that our programs calculate reliable results.
3.2 Comparison with the BLW Method
In the BLW method, as emphasized by Mo,[10-15] it is only the charge-transfer interaction energy to be excluded between the isolated groups. In fact, it is unable and impossible for the BLW method to exclude the orbital charge-transfer and exchange interactions both from the localized geometry. Certainly, the BLW method is fundamentally different from ours.
Table 2. The values of the extra stabilizing energy (ESE) of benzenewere obtained from our 2010 program at the RHF, MP2, CISD, CCSD and DFT theoretical levels (energy unit in kcal/mol

The overall average of all values listed in the Table is -35.0 kcal/mol. a. Perdew-Burke-Ernzerhof 1996 exchange, no correlation. b. HF exchange, Perdew-Burke-Ernzerhof 1996 nonlocal + Perdew-Wang 1991 LDA correlation. c. Perdew-Burke-Ernzerhof 1996 exchange, Perdew-Burke-Ernzerhof 1996 nonlocal + Perdew-Wang 1991 LDA correlation. cc- PVTZ, Dunning’s correlation consistent basis set (triple-zeta).
Table 3. The single and double bond lengths rC-C and rC=C in the localized geometry of allyl cation CH2=CH-CH2+, and the energy difference [E(G) - E(GL)] between the ground state (G) of allyl cation and its GL geometry. The values of these quantities were obtained, respectively, from our programs (including our 2007 and 2010 programs) and from BLW method. 
a. The values obtained from BLW were cited from refs 14 and 15. For the ground state, the values of the molecular energy are -116.19321 (HF/6-31G*) and -116.97221 (B3LYP/6-31G*) hartree,and the bond lengths rC-C and rC=C are 1.373 and 1.373 Å (RHF/6-31G*), and 1.385 and 1.385 Å (B3LYP/6-31G*).
In the case of a carbocation such as CH2=CH-CH2+, there are only pi-orbital charge-transfer interactions (without the orbital and spatial exchange interactions) between the CH2=CH- and -CH2+groups, making it a useful molecule to allow a comparison of our 2010 and 2007 programs with the BLW method. In this special case, as shown by the data listed in Table 3, these three programs provided the allyl cation CH2=CH-CH2+ with the same GL geometry in which the pi systems are localized on the CH2=CH- and -CH2+ groups. At the HF/6-31G* level, for example, the three values of the energy difference [E(G) – E(GL)] all are equal to –37.8 kcal/mol, and it is stabilizing.
3.3 Comparison with Morokuma’s Intermolecular Energy Decomposition Analysis
The geometry of the complex NH3-BH3 was fully optimized at the HF/6-31G* level, and its molecular energy was calculated as -82.61182 hartree. Our 2010 program and Morokuma’s intermolecular energy decomposition analysis[7, 16, 17] were then used to perform a restricted single point energy calculation at the fully optimized geometry of NH3-BH3. The restricted single point energy calculation gave NH3-BH3 a localized electron state (LES) in which all of the molecular orbitals, as well as electrons, were completely localized on their respective monomers and the geometry of the complex remained unchanged. Both programs gave a LES with the same molecular energy (-82.73808 hartree). So the energy difference [E(G) - E(LES)] between the G and LES is 79.2 kcal/mol, and it is destabilizing.
4. Conclusion
In a localized geometry optimized by using our 2010 program, all the energy effects, arising from the orbital charge-transfer and exchange interactions and from the spatial exchange interaction between the isolated groups, have been excluded, meaning that the pi molecular orbitals and pi-electrons have all been completely localized on their corresponding groups. As a result, the ESE of benzene can be evaluated at the DFT, HF and post-SCF levels, and various basis sets have a slight effect on the value of the ESE. For benzene, the B3LYP/6-31G* value of -36.3 kcal/mol can be considered equal to the experimental value of 36.0 kcal/mol .
Based on the comparisons between our procedure, Morokuma’s energy decomposition analysis and the BLW method, it has been confirmed that our 2007 and 2010 programs calculate reliable results and the BLW method is only a special case of our program. The calculated GL and GE-m localized geometries do not correspond to any real state of a physical system. Therefore, the molecular energy of a localized geometry can be lower or higher than that of the actual system,[18,19] and [E(GE-m) – E(GL)] > 0 is reasonable.
So far, Maksić’s comments, completely being out of his personal feeling, have been formally refuted, and his mistakes have already been detailed in our 2008 response.[6]
References
1. Schleyer, P. v. R., Chem. Rev. 2001,101, 1115.
2. Bao, P; and Yu, Z. H. J. Phys. Chem. A 2007, 111, 5304.
3. Kistiakowsky, G. B.; Ruhoff, J. R.; Smith, H. A.; Vaughan, W. E. J. Am. Chem. Soc. 1936, 58, 146.
4. Maksić, Zvonimir B. J. Phys. Chem. A, 2009, 113, 788.
5. The original version of the Maksić’s comment manuscript has been posted on the Blog: http://www.sciencenet.cn/m/user_content.aspx?id=207637.
6. Our response manuscript has been posted on the Blog:
http://www.sciencenet.cn/m/user_content.aspx?id=48687
7. Kitaura, K.; Morokuma, K. Int. J. Quantum Chem. 1976, 10, 325.
8. Bader, R. F. W.; Stephens, M. E. J. Am. Chem. Soc. 1975, 97, 7391.
9. Bao, P; and Yu, Z. H, J. Comput. Chem. 2011, 32, 248.
10. Mo, Y. R.; Lin, M. H.; Wu, W.; Zhang, Q. E. Acta Chem. Sin. 2000, 58, 218.
11. Mo, Y.; Peyerimhoff, S.D. J. Chem. Phys. 1998, 109, 1687.
12. Mo, Y.; Zhang, Y.; Gao, J. J. Am. Chem. Soc. 1999, 121, 5737.
13. Mo, Y. J. Chem. Phys. 2003, 119, 1300.
14. Mo, Y. J. Org. Chem. 2004, 69, 5563.
15. Mo, Y.; Song, L.; Lin, Y. J. Phys. Chem. A 2007, 111, 8291.
16. Morokuma, K.; Kitaura, K. "in Chemical Applications of Electrostatic Potentials", Politzer, P.; Truhlar, D.G. Eds. Plenum Press: New York, 1981, 215.
17. Morokuma, K. J. Chem. Phys. 1971, 55, 1236.
18. Morokuma, K.; Kitaura, K. Chemical Applications of Electrostatic Potentials, Politzer, P.; Truhlar, D. G., Eds.; Plenum Press: New York, 1981, p. 215.
19. Kollmar, H. J Am Chem Soc 1979, 101, 4832.
(To be continued)
https://blog.sciencenet.cn/blog-94786-421874.html
上一篇:Chapter 5 (4): Formally Refuting the Maksić’s Comment (1)
下一篇:我在Amazon发表的英文专著的目录