质量缺失之谜

左 芬

2018年4月

（按：写作本文的时候，并没有想过要翻译 Priyamvada Natarajan 关于暗物质的文章，或是翻译 Milgrom 的采访，所以在这里引用的都是英文原文。）

当前物理学面临的最大挑战是如何统一量子力学与广义相对论。有人认为，这其中最大的难点在于，未来很长一段时间内可能都没法找到直接的实验证据来推动理论的发展。对此，我不敢苟同。事实上，天文与宇宙学的观测已经远远领先于理论的发展，这突出地表现在两个现有理论框架完全不可解的观测结果上，即所谓的宇宙加速膨胀（俗称暗能量）和星系（团）质量缺失（俗称暗物质）上。我不知道别的物理学工作者是如何与之安然相处的。在我，是如鲠在喉，如芒刺背，惶惶不可终日。或者，像 Birdman 说的，“is kind of starting to feel like a miniature, deformed version of myself that just keeps following me around and, like, hitting me in the balls with a... like, a tiny little hammer.”在我看来，把她们跟上世纪初著名的以太疑难与黑体辐射的紫外灾难相提并论，是丝毫不为过的。我们知道，以太疑难不曾导致以太的发现，而是狭义相对论的建立；黑体辐射紫外灾难的解决也不曾导致某种反辐射或者暗辐射的发现，而是量子力学的建立。同样地，或许我们也不应该仅仅预期某种暗能量和暗物质的发现，而应考虑到其他的可能。借用我们近期读到的 Priyamvada Natarajan 在“Dark Matter Is Either Like Neptune or Like Vulcan”一文中的话，就是: It may go the way of ether...

在这两个问题中，后一个更加通俗易懂，所以我们先来讲讲。（前一个问题将在下篇短文“De Sitter 之谜”中讨论。）有人会质疑，现存理论体系中的暗物质涉及的范围远远超越星系质量缺失的问题，你如何解释？对此我借用 Milgrom 和 Verlinde 的回答：在我们完全理解星系（团）的质量缺失问题之前，暂时先把其他问题放下。用历史的语言来说，就是：在完全理解黑体辐射的 Planck 公式之前，我暂时没有能力解释光电效应和原子的线状光谱。 请注意，我一再地提到黑体辐射和 Planck 公式，是别有用心的！

星系质量缺失的问题可以非常直观地从星系的旋转曲线看出，如下图：

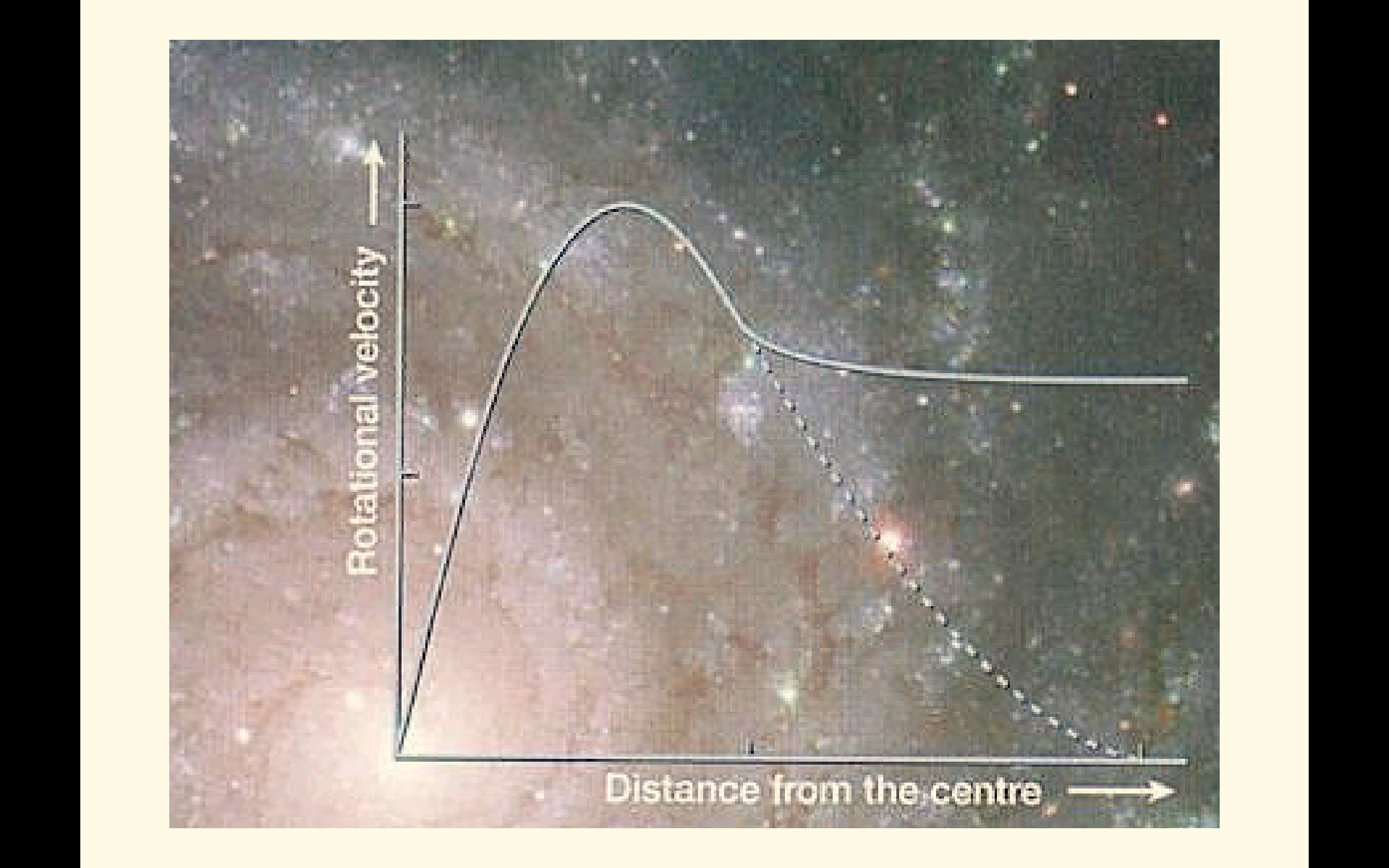
图中虚线对应着Newton引力（作为广义相对论在此情形下很好的近似）的预言，而实线是观测结果。在星系外围，由于Newton引力反比于半径平方，而离心力反比于半径，理论上旋转速度应随半径增大而减小。在太阳系中的确如此，离太阳最近的水星（Mercury）运行速度超过每小时十万英里，而最远的海王星（Neptune）仅为每小时一万英里左右。然而，当我们把尺度从恒星外推到星系时，却发现旋转曲线在下降过程中突然变平坦了，甚至延伸到非常遥远的距离。速度的异常增大导致离心力的增大，使得我们需要更强的引力去平衡；似乎星系中存在着大量的未知物质，产生了额外的引力束缚住了星系外围。是这样吗？

让我们再一次回到太阳系，看看我们当时是如何探索太阳系的。这里我们重复一下 Priyamvada Natarajan在“Dark Matter Is Either Like Neptune or Like Vulcan”一文中的内容。19世纪早期，天文学家们注意到新发现的天王星（Uranus）偏离预期轨道。人们猜测天王星可能受到未知行星的牵引。很快法国数学家Urbain Le Verrier就算出未知行星的位置。的确，天文学家们在那儿发现了海王星（Neptune）。Le Verrier同时也注意到水星轨道的偏离，于是猜测水星和太阳之间也存在某个未知行星（Vulcan），并计算出其可能的位置。然而，这一次，天文学家们什么也没有发现。现在我们知道，水星的轨道异常是因为作为广义相对论近似的Newton引力自身已经失效。那么，反常的星系旋转曲线到底是因为某种未知的物质（暗物质）的引力，还是广义相对论自身失效了呢？“Is dark matter like Neptune or like Vulcan?”

为了回答这个问题，我们需要仔细分析大量星系的旋转曲线，并从中找出共同特征。首先，曲线的转折点出现在什么地方？Milgrom 在他的访谈“The Physicist Who Denies that Dark Matter Exists”中详细描述了他在1980年前后的分析过程。通过对各种参数的一一排查，他有了一个惊人的发现：所有的曲线都在加速度减小到同一个临界值时发生转折。更加令人惊异的是，这个临界加速度只依赖于整个宇宙的尺度！我是从 Lee Smolin 的科普书“The Trouble with Physics: The Rise of String Theory, the Fall of a Science, and What Comes Next”(2006年出版，湖南科学技术出版社2008年出了由李泳翻译的中文本，即《物理学的困惑》)中首次读到这个结果的，当时只觉得“石破天惊，云垂海立”。 Smolin在书中表达了类似的反应。我几乎不敢相信这竟然是真的！而且我也从未在任何研究暗物质的同行中听到过这样的表述，回想起来真是悲哀。很难相信某种未知的物质（暗物质）会依赖于宇宙尺度；或者说，如果她依赖于宇宙尺度，我们更应该把她看做时空本身，而非物质。从这个角度来说，Dark matter may go the way of Vulcan, rather than Neptune...

那么，这个临界加速度是多少呢？为了说明这一点，我们需要补充一点宇宙学的内容。作为一个宇宙学方面的门外汉，我只能胡诌。1929年前后，Hubble发现了星系相对退行速度大致正比于她们之间的距离，即所谓的Hubble定律。正比系数我们现在称为Hubble常数H。我们不是历史学家，所以对在这一发现中做出过重大贡献的其他科学家略过不提。Hubble 定律暗示我们，宇宙在膨胀，从而导致了星系间越来越大的相对速度。如果在一个惯性系里考虑，狭义相对论告诉我们，相对速度不能超过光速。我们把退行速度达到光速c的那个距离定义为Hubble距离L，并用她来代表宇宙的某种特征尺度。 粗糙一点地说，你可以把她看成宇宙的半径。以光速c在宇宙外围旋转会感受到一个小得可怜的离心加速度，我们把她叫做 a0（=c^2/L）。你可以想象一下，虽然光速很快，但是放到整个宇宙的尺度，她还是会疲劳的。正是这个微弱的加速度 a0 ，标志着星系旋转曲线的转折点。

得到转折点之后，我们进一步分析转折后的曲线。这一步就容易多了，因为她几乎就是一条直线嘛。为了得到直线，Milgrom 尝试了两种方式，修正 Newton 第二定律或者 Newton 引力。在我看来，似乎后一种在逻辑上更为合理，所以我们介绍后者。为了消除Newton引力与离心力对半径的不同依赖，我们需要修正Newton引力的平方反比律为直接的反比律。这一点很容易实现，因为我们现在有了两个加速度，Newton引力加速度和常值的临界加速度。为了消除平方，只需要取二者的乘积再开方即可。其结果是，极限速度正比于星系质量的四次方根，这正是著名的实验定律：重子Tully-Fisher关系（1977）。为了与现存实验不违背，我们需要假定这样的修正只发生在引力加速度小于临界加速度 a0 时。人们把 Milgrom 修正后的Newton力学/引力称为MOND（Modified Newton Dynamics）。正因如此，Milgrom自称是继Planck和Einstein后第三个修正Newton力学的人。

但是仅仅拟合旋转曲线是远远不够的，这背后深层次的原理是什么？为什么宇宙学尺度会出现在小小的星系中？ Milgrom并没能告诉我们。事实上目前似乎还没有人真正知道原因。但我们可以回顾历史，去寻求一些启示。我们惊讶地发现，星系旋转曲线的异常与历史上著名的黑体辐射谱的紫外灾难有着惊人的相似之处。

我们回顾一下黑体辐射。在给定温度下，黑体辐射的能量密度随频率变化的对数-对数图如下：

从经典统计物理和电磁理论出发，可以证明辐射能量密度正比于频率的平方，唯一的正比系数由光速c、玻尔兹曼常数k以及温度T决定。这在双对数图上表现为图中红色的直线，即 Rayleigh-Jeans 公式。Rayleigh-Jeans公式能很好地描述黑体辐射的低频实验数据。但在高频（即短波，紫外）区，预言的能量密度持续增大，导致积分后的总能量为无穷大（从而不可能正确）。这就是著名的紫外灾难。实验观测结果表明，随着频率增长，辐射能量陡然下降，并在高频时趋于零。高频区的能量压低可以简单地用一个指数因子模拟，这就是Wien的半经验公式（图中蓝线）。在 Wien 公式中，除了整体正比系数外，能量密度在指数上出现了第二个参数。注意Wien公式在低频下并不回到 Rayleigh-Jeans 公式，从而与实验数据相违背。为了弥补两者分别存在的缺陷，Planck天才般地猜到了一个公式，可以光滑地从低频的 Rayleigh-Jeans 公式过渡到高频的 Wien 公式，从而完美地刻画了所有频段的能量谱（图中绿线）。相比于 Rayleigh-Jeans 公式只依赖于c、k、T，Planck公式还出现了一个额外的普适常数，这就是我们现在耳熟能详的Planck常数 h。为了进一步解释这一公式以及 h 的物理含义，Planck 提出了辐射的量子化概念，并最终导致了量子力学的建立。

如果我们把这两个物理图像放到一起对比，会发现很多惊人的相似之处。星系旋转曲线中的 Newton-Einstein预言对应着这里的 Rayleigh-Jeans 公式， Milgrom 修正后的速度曲线（直线）对应着这里的 Wien 公式，极限加速度a0（或者Hubble尺度L）对应着这里的Planck常数h。可是，完整的 Planck公式以及量子化解释呢？暂时还没有人知道。从这一点来看，Milgrom 以 Planck 和 Einstein 自许，似乎还远远没有做到。他还仅仅完成了Wien的工作。 Verlinde 近年来竭力想完成Milgrom未完成的工作，但现在看来，也还是远远不够。

事实上，Milgrom 修正Newton力学的提法，其格局似乎有些过小。如果我们严格对待以上对比的话，Hubble尺度L就应该是另一个Planck常数了。这样的话，我们在通常微观世界的量子化之外，在宇宙的宏观世界又发现了第二种量子化。如果这样的猜测成立的话，我们需要做的不是修正 Newton，而是同时修正Planck 和Einstein。这样的猜测是否有可能是对的呢？我们将在下篇短文“De Sitter 之谜”中继续讨论。

（补记：文中提到的 “De Sitter 之谜”一文因为涉及一些艰深的现代数学理论，一直没有完成。）