博文

Zmn-0934黄汝广: 关于悖论与反证法中隐性假设的探讨

已有 878 次阅读 2023-1-31 12:04 |个人分类:数学啄木鸟|系统分类:论文交流

Zmn-0934黄汝广: 关于悖论与反证法中隐性假设的探讨

【编者按。下面是黄汝广先生的文章。现在发布如下，供网友们共享。请大家关注并积极评论。另外本《专栏》重申，这里纯属学术讨论，所有发布的各种意见仅代表作者本人，不代表本《专栏》编辑部的意见。《专栏》中有些文章发扬了啄木鸟精神，对一些错误的观点和言论进行了说理的批评。但请大家注意，也有些有严重错误的文章在这里发布，就是为了引起和得到广大网友们的评论。不要以为在这里发布的文章都是正确无误的。】

关于悖论与反证法中隐性假设的探讨

黄汝广

（深圳南天电力有限公司，广东深圳 518040）

摘要

隐性假设是破解悖论以及分析反证法证明是否有效的关键，为确定导致矛盾的真正根源所在，有必要尝试将现代因果关系分析技术的一部分引入反证法，从而减少显性假设成为“替罪羊”风险。

关键词

说谎者悖论；实质蕴涵怪论；反证法；隐性假设；康托尔；戴德金分割；因果分析

在《悖论的消解》一书中，文兰先生提出：“悖论是反证法的未被察觉的掐头去尾。一个悖论，一旦被发现隐蔽的假设，并由此补上开头句和结尾句写成反证法，可以说就被彻底解决了。”

这种观点是非常富有启发性的，但是可能有点过于乐观了。实际上，悖论问题的彻底解决并不仅仅在于某一个甚或几个隐性假设的发现，其真正的关键在于：这被发现的隐性假设是否是导致矛盾的真正原因所在。同样的道理，如果反证法中所谓矛盾的根源并不在于那个明面上的假设，而是在于未被察觉的隐性假设，那么这个反证法证明就是无效的。

当然，隐性假设也不是仅仅存在于悖论或反证法中。比如，萧文强《数学证明》与路沙*彼得《无穷的玩艺》都提到一个例子，用于说明有穷不能随意推广到无穷的观点：将斜边n等分，并连接成阶梯折线，则当n趋于无穷时，可以得出斜边等于二直角边之和的结论。两个数学家同时采用这样一个例子，真是让人惊讶万分：说实话，之所以得出当n趋于无穷时斜边等于二直角边之和的结论，错误其实并不在于以有穷推无穷，而在于两位数学家使用了错误的隐性假设，也即对于无穷小三角形，其斜边等于二直角边之和，勾股定理不再成立！

1. 说谎者悖论的隐性假设

笔者认为，“说谎者悖论”的推理就至少需要以下两个隐性假设作为前提条件：（1）“本语句为假”是一个命题，否则它也就无所谓真假，根本无从判断；（2）“本语句”指代“本语句为假”这种否定式的自指涉是合法的，否则推理根本无法进行下去。

在承认隐性假设（2）的前提下，文先生认为“本语句为假”并不是单纯的一句话，其中“本语句”这个代词是一个句变元X，而“本语句为假”实际上是一个句方程“X:=XF”（其中“:=”表示“意指”，“F”表示“为假”，即“X意指X为假”，所对应的布尔方程即“X= ~X”）。有了这个说谎者方程，再补上“假设方程有解”作开头，则说谎者悖论还原为一个反证法，其结论为：说谎者方程没有句解。

然而，问题真的就此得到了彻底解决吗？实际上，我们还不妨进一步问：为什么说谎者方程没有句解？仔细追究下去，矛盾的根源其实在于推理中使用了否定式的自指涉方法，从而导致说谎者悖论对应布尔方程“X= ~X”，而这与同一律“X= X”明显相矛盾；换言之，否定式的自指涉方法已经违反了逻辑学的基本定律，因而是不合法的。我们不能因为肯定式的自指涉不构成矛盾，就理所当然地认为否定式的自指涉也不构成矛盾。

实际上，说谎者悖论的真正关键点在于“本语句”这个代词仅仅是一个变元X，因此，“本语句为假”在本质上只不过是一个命题函项，也即“X为假”。而且很显然，这里的变元X必须用具有真值的命题来进行赋值，但由于命题函项“X为假”自身并不是一个命题，当然也就不能用来为X赋值了。或者换句话说，说谎者悖论的自指涉是不合法的。从这个意义上讲，肯定式的自指涉“本语句为真”虽然不构成矛盾，但仍然是不合法的。

退一步讲，即使我们可以用“X为假”来为X赋值，但是无论我们迭代赋值多少次，变元X都不可能被削去，所得的结果仍然还是一个命题函项而不是一个命题，因此它也就无所谓真假。然而，否定式自指涉的命题函项在经过迭代之后，会发生质的变化：比如，“本语句为假”迭代一次可得“‘X为假’为假”，但由于双重否定为肯定，实际上就得到了一个与原命题函项完全矛盾的命题函项——“X为真”。这正是否定式自指涉方法构造“矛盾”的秘密所在，也是张铁声先生的“多义句”解悖方案中为什么产生多义的原因所在。

按照文先生的解悖方法，如果要否定上述隐性假设（1），“说谎者悖论”就应该还原为如下反证法：“假设‘本语句为假’是一个命题，则其真值要么为真，要么为假：令其为真，则……，矛盾；令其为假，则……，矛盾。因此，‘本语句为假’不是一个命题。”

如果要否定隐性假设（2），“说谎者悖论”就应该还原为如下反证法：“假设否定式的自指涉是合法，将其用于‘本语句为假’：当其为真时，则……，矛盾；当其为假时，则……，矛盾。因此，否定式的自指涉是不合法得。”

实际上，否定式的自指涉方法本质上也是一种偷换概念，把本质上不同的东西完全混为一谈了。如果令Q=“本语句”，那么带入“本语句是假的”后可得“Q是假的”，很显然，“Q”与“Q是假的”是完全不同的。因此，“本语句是假的”不可能还是Q，必须用另外的符号表示，不妨令Q1=“本语句是假的”，可是说谎者悖论中却认为Q1=Q。

要言之，说谎者悖论的根源在于有意或无意的偷换概念：（1）硬把一个根本不是命题的句子当做命题来判断其真假,；（2）否定式自指涉方法违反了矛盾律，从而将不同的东西混为一谈。

笔者认为，几乎一切所谓的悖论，其根源都在于：要么有意或无意中偷换了概念，要么概念或方法的使用超出了其适用范围，甚至于直接违反了基本定律或常识。更具体讲，它们通常表现为一个或几个事实上根本不成立的隐性假设，如此一来，以它们作为前提所推论出的“矛盾”当然就是不可靠的，因此，所谓的悖论其实只是佯谬而已。

2. 实质蕴涵怪论的隐性假设

通常而言，我们所谓的蕴涵都有“推出”的含义，而实质蕴涵所定义的“→”只不过是一个连接词，根本没有“推出”这一含义，很多逻辑学教材也都强调了这一点。但奇怪的是，作者们似乎很快又忘记了这一点，竟理所当然地把实质蕴涵的所谓重言式都视为有效推理模式，这一做法其实是隐含地把“推出”含义强加给了单纯的连接词“→”，从而将“实质蕴涵”偷换概念为了“有效推理”。

其实，我们只要看看最早公理化的欧几里得几何就明白，推理都是基于公理及概念间的内涵关系，而与纯粹基于真假值的实质蕴涵没有任何关系。一个最基本的事实就是，如果“若P则Q”为真，那么它就是一个定理，而一个定理必须要有一个证明；但是，证明只能靠推理得到，而不是靠摆弄P与Q的真值得到。

命题当然都有真值，但真值并不是命题的全部，命题还有内涵，而且某种程度上来说，正是命题的内涵决定了其真值。既然命题具有真值这一属性，我们自然可以通过真值表来对命题进行一些研究，但是，如果企图通过真值表来解决命题逻辑的一切问题，那就完全不切实际了。莫绍揆先生早已经指出：“P蕴涵Q”不是真值函数，不能只靠P与Q的真假而决定其真假，事实上，它指出P与Q之间是有一定的意义关系的。

我们知道，如果命题P与Q构成有效推理“P→Q”，那么复合命题“~P∨Q”为真；但是复合命题“~P∨Q”为真，“P→Q”却未必能构成有效推理（比如P=“所有人都是要死的，并且猫不是人”，Q=“猫是要死的”）。因此，复合命题“~P∨Q”为真，只是命题P与Q构成有效推理“P→Q”的一个必要条件，但不是充分条件。

然而，实质蕴涵的定义却是：若“~P∨Q”真，则“P→Q”真；若“~P∨Q”假，则“P→Q”假。这个定义表明，“~P∨Q”为真是实质蕴涵“P→Q”为真的充要条件，因此，实质蕴涵“P→Q”与有效推理“P→Q”是两个不同的概念。但是，当质蕴涵的重言式都被理所当然地视为有效推理时，偷换概念就发生了。在偷换概念后，定义的后半部分仍然适用，也即“~P∨Q”为真是有效推理“P→Q”的必要条件，这也是实质蕴涵运用于日常推理，有时候看着很合理的原因所在；但定义的前半部分，也即“~P∨Q”为真是有效推理“P→Q”的充分条件，却不再适用，这正是诸多实质蕴涵怪论的根源所在。

关于实质蕴涵怪论，各种论著可谓汗牛充栋，但似乎都不把“P→P∨Q”或者“P∧Q→P”看作怪论，而是理所当然的有效推理（假如我们约定“∨”是“异或”而不是“可兼或”，那么“P→P∨Q”的无效性就显而易见了）。然而，在笔者看来，这两者即使算不上怪论，它们对于推理也没有任何意义：因为无论Q的真值与内涵如何，它对于“P→P∨Q”都是无关紧要的，完全是画蛇添足。试想，如果欧几里得在《几何原本》的每一个定理中，都加上一句“或者欧几里得是伟大的几何学家”，那该有多讨厌。在“P∧Q→P”中，Q也同样多余，既然P可以直接推出P，那就没有必要再引入其它条件，毫无关系甚至矛盾的条件就更加没有必要。依据著名的奥卡姆剃刀原则，这些“蛇足”都是应该被剔除的。

实际上，即便“P→P”都是画蛇添足，因为这种同义反复的废话，对于实际的推理也没有任何用处。一个著名的例子，即塔尔斯基的所谓“真”之定义——“雪是白的”为真，当且仅当雪是白的。这个定义完全是废话，没有一点的可操作性：试想，一个不知道雪是何物的人，如何根据这个定义来判定“雪是白的”到底是真还是假呢？这根本是不可能的。

因此，一切多余的、不具有可操作性的概念或定义，都应该被剔除。事实上，一个概念或定义即使具有可操作性，它往往也只适用于一定的范围，一旦超出其适用范围，谬误往往也就随之而来。

3. 实质蕴涵怪论对于反证法的侵蚀

塔尔斯基曾信誓旦旦地声称：“正是在这个简单的实质蕴涵上面的逻辑学，已被证明是最复杂精细的数学推理的满意基础。”然而，事实却恰恰相反：正是这个简单的建基于实质蕴涵之上的逻辑学，在侵蚀着最复杂精细的数学推理的基础，把反证法带入了极大的误区，以至于“~P→P，所以P”被公认为反证法的有效模式。

在《逻辑代数初步》一书中，莫绍揆先生站在初学者的角度，提出一个古人其实早已有过的想法：如果由非P推出P，既有P又有非P，这不是作推导的人自己陷于了矛盾吗？在亚里士多德看来确实如此。但是莫先生认为，这种想法是不对的，并且给出了一个由非P推出P的例子——

已知定理（甲）：若质数h能整除a·b，且不能整除a，则h必整除b。

需要证明定理（乙）：若质数h能整除a²时，则h必整除a。

证明：“当把a²写成a·a，与（甲）相比较，可知：如h不能整除a，则h必整除a，这便由~P而推出P，故P=t而定理得证。”

原书这里写的有点过于简略，但还不至于让人误解。不过，非常遗憾的是，这个证明完全是无效的。实际上，定理（甲）的成立需要一个限制条件，也即a≠b，但被不当省略了。不妨假设当a=b时，定理（甲）仍成立，把b用a替换，可得：若质数h能整除a·a，且不能整除a，则h必整除a。很显然，当a=b时，定理（甲）自身已经构成矛盾，因而是不可能成立的！

所以，定理（甲）的完整表述应为：若a≠b，且质数h能整除a·b，但不能整除a，则h必整除b。而莫先生给出的上述证明，在运用定理（甲）时，已经违反了前提条件a≠b，属于典型的“若P则Q，非P，所以Q”式否定前件谬误；所谓由非P推出P，完全是因为没有搞清楚定理的适用范围，从而误用定理所造成的结果。

实际上，莫先生在书中采用了麦柯尔的蕴涵定义“P∧Q=P”（或“~P∨Q=t”，或P∧~Q= f），认为它比较符合直观，并解释说：这里的“f”并不是简单的假，而是指P∧~P，是“自相矛盾”，是“永假”，比简单的假要强得多；同理，“t”也并不是简单的真，而是指P∨~P，是“永真”，比简单的真也强得多。

然而，如此一来，反证法模式“~P→P，所以P”，其实就不是简单地证明P真了，而是证明P永真，比简单的P真强太多了。实际上，亚里士多德早就指出：如果命题Q与其否命题~Q都可以推出命题P ，最终将导致~P推出P，这是荒谬的。但是，涅尔夫妇认为：恰恰相反，这等于证明了命题P是绝对必然的。笔者认为，正确的理解应该是：无论前提条件Q是否成立，命题P均成立，这并不表明P是绝对必然的，而只是表明P与Q（或~Q）无关；或者换句话说，Q（或~Q）在推理中实际上都是应该剔除的“蛇足”。

“~P→P，所以P”的另一个变形模式是“~P→Q，~P→~Q，所以P”，这种模式或许有一个好处，即更容易引起人们思考：既然相同的前提推出了不同的结论，那么两个推理在方法上肯定会有所不同，为什么不可能是其中一种方法甚或两种方法都出了问题呢？事实上，正常的思维方式就应该是在两者不同的条件中来寻找结果不同的原因。

如果方法确实没有问题，那就只可能~P 为复合命题，也即~P=M∧~M，而“~P→Q，~P→~Q”实际上应该是“M→Q，~M→~Q”，也即两个推理的前提其实并不同。不过，明面上直接假设一个矛盾式的很少见，通常都是利用否定式自指涉方法来构造隐性的矛盾式，这正是黄展骥先生的“复合命题谬误”解悖方案。

笔者认为，一个标准的反证法模式应该是“~P∧E∧F→Q，~Q，所以P”；其中~P是假设，E是推理过程中用到的其他前提，~Q是一个独立于假设~P的已知事实（即~Q为公理或定理的结论，并且不以~P或P为条件），F是证明所用的方法。如果对于每个推理前提都不带任何偏见的话，严格的结论应该是“P∨~E∨~F”；只有在证明前提E为真，并且方法F没有问题的情况下，才可以进一步分离出结论P。这里之所以把方法F单独列出来，是因为一些所谓的方法——比如康托尔对角线法——确实值得商榷，而方法自身导致的矛盾，不应该用来否定~P。

不过，即使方法F正确，反证法还是存在隐性假设的问题；当然，这个问题在直接证明中也同样存在，但对于反证法似乎更为突出。如果一个证明存在隐性假设，而假设本身可以另外得到证明，则整个证明仍可挽救；但如果隐性假设本身是错误的，且在证明中必不可少，那么整个证明就很难补救了。在反证法中，如果导致矛盾的根源是一个错误的隐性假设，但并没有被意识到，那么结果就很可能是显性假设~P成为替罪羊。对于那些在推理过程中利用了否定式自指涉的反证法，这似乎是一个必然的结果。

4. 实数不可数的康托尔反证法中的问题

康托尔关于(0,1)不可数的反证法论证大致如下：(0,1)内的任何实数均可用十进制无限小数表示，假设(0,1)可数，则它与自然数一一对应，可得如下一个无穷序列

1→0.a₁₁ a₁₂ …a_1n …

2→0.a₂₁ a₂₂ …a_2n …

……

n→0.a_n1 a_n2 …a_nn …

……

然后构造数b=0.b₁ b₂ …b_n …（当a_nn=1时，取b_n=2；当a_nn≠1时，取b_n=1）。康托尔认为，b属于(0,1)却不属于该序列，矛盾，故(0,1)不可数。

关于康托尔这个证明，很多人都指出了问题所在。其中最形象的说法是：康托尔的对角线法只适用于“正方形”的序列矩阵，而上述无穷序列矩阵实际上却是“长方形”的，已经超出了方法的适用范围，因而推理无效。事实上，康托尔所谓的不可数结论，恰恰就表明了上述无穷序列矩阵是“长方形”的而非“正方形”的，因此对角线法不适用。

然而笔者认为，这个证明中一个更严重的问题，却是康托尔对“一一对应”概念的随意泛化，也即概括原则的滥用（属于归纳逻辑），本质上也是偷换概念的一种表现。在数学上，“一一对应”需要由确定的函数关系或对应生成法则来完成，而不是把两个集合的元素随意地连线配对，或者用一个集合的元素来为另一个集合的元素进行编号。按照这个要求，上述序列中“n→0.a_n1 a_n2 …a_nn …”的真正含义应该是，存在一个确定的法则F，使得F(n)= 0.a_n1 a_n2 …a_nn …，所以，即使不考虑对角线法是否适用的问题，康托尔的正确结论也应该是：不存在一个确定的函数关系F，通过它由全体自然数可以生成全体实数。

为了看出这里的区别，我们来看一个例子。首先，我们构造一个实数集合A，其元素个数与自然数集N完全相等，但是其每一个元素都是随机生成的；很显然，按照康托尔泛化后的“一一对应”概念，自然数集N与集合A是“一一对应”的。然而事实却是，集合A的元素都是随机生成的，不可能存在一个确定函数关系F，使得自然数集N与集合A“一一对应”，否则集合A就不是随机生成的了！

众所周知，按照康托尔泛化后的“一一对应”概念，自然数集N与素数集P也是“一一对应”的：对于自然数集N实施筛法，得到所有素数，然后按依次编号1,2,3……；然而，这并不意味着存在一个确定的函数关系或法则F，使得F(n)=p_n。实际上，如果我们仔细考察一下上述操作，就会明白:要得到素数p_n，筛法的真正实施对象是某个合适的自然数子集Nn，素数p_n并不仅仅由n决定,因此，真正的函数关系F至少应该是二元的，也即F(Nn，n)=p_n。所谓的“一一对应”，其实只不过是通过概念泛化，二元关系被偷换概念成了一元关系而已。

同样的道理，自然数集N与其幂集P(N)，也不可能存在真正数学意义上的“一一对应”关系。因为得到幂集P(N)的所有元素的操作，其实施对象决不仅仅是一个单一的自然数，换言之，如果存在确定函数关系的话，它也一定是多元关系。

5. 一个实数不可数的新反证法及其无效性的分析

网友matrix67介绍了一个证明实数不可数的新方法，当然也是反证法，不是太复杂，全引如下：

“最近，Matthew H. Baker找到了证明实数区间是不可数集的一种新方法。这种方法同原来的方法完全不同。新的证明方法从一个博弈游戏出发，在两个不同的数学领域间建立起了联系，非常具有启发性。
A和B两个人在实数区间[0,1]上玩一个游戏。首先，A在(0,1)之间选一个数a1，然后B在(a1,1)里选一个数b1；接着，A在(a1,b1)之间选一个数a2，然后B在(a2,b1)里选一个数b2……总之，以后A和B轮流取数，选的那个数必须位于前面两次选的数之间。可以看到，序列a1, a2, a3, ...是一个单增的有界序列，因此游戏无限进行下去，数列{an}最终会收敛到某一个实数c。游戏进行前，A和B约定一个[0,1]的子集S，规定如果最后c∈S，则A胜，否则B胜。

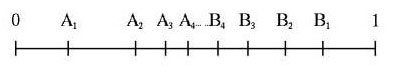
Baker发现，如果S集为可数集的话，B肯定有必胜策略。如果S集可数，那么B就可以把S集里的数排列成一个序列s1, s2, s3, ... 。B的目标就是让序列{an}的极限不等于S集里的任一个数。考虑B的这样一个游戏策略：当B第i次选数时，如果选si合法，那么就选它（这样序列{an}就不能收敛到它了）；否则如果这一步选si不合法，那就随便选一个合法的数（此时序列{an}已经不可能收敛到si了）。这种策略就可以保证A选出的数列的极限不是S集里的任一个数。
有趣的事情来了。假如A和B约定好的S集就是整个实数区间[0,1]，那么B显然不可能获胜；但如果[0,1]是可数集的话，B是有必胜策略的。于是我们就知道了，[0,1]是不可数集。”

然而，这个反证法证明真是有效的吗？

首先，根据游戏规则，数列{an}的极限c必定属于[0,1]，因此，不管[0,1]是否是可数集，只要约定S=[0,1]，A就必胜；也不管[0,1]是否是可数集，只要约定S=Ø，B就必胜。很显然，B要实现其必胜的目标，也即“让序列{an}的极限不等于S集里的任一个数”，在对S集进行约定时，必须要求S⊂[0,1],也即S只能是[0,1]的真子集，这是他必胜的先决必要条件。

所以，Baker证明的所谓“B必胜定理”的完整表述应该是：“如果S是可数集，并且S⊂[0,1]，则B肯定有必胜策略。”要注意的是，对于这个定理，否定其后件“B肯定有必胜策略”，可以推出的结论应该是“或者S不是可数集，或者S=[0,1]”，而不是唯一的“S不是可数集”。

我们再来看Baker所谓的矛盾：“假如A和B约定好的S集就是整个实数区间[0,1]，那么B显然不可能获胜；但如果[0,1]是可数集的话，B是有必胜策略的。”很显然，在S=[0,1]的约定下，“B显然不可能获胜”完全成立。但是，在这个约定前提下，“S⊂[0,1]”已经不再满足，此时即便[0,1]是可数集，“S是可数集，并且S⊂[0,1]”也仍然不满足；根据完整的“B必胜定理”，不可能有效地推出“B是有必胜策略的”。因此，Baker所谓的矛盾完全是子虚乌有的，是无效推理所导致的假矛盾。

或者换一种角度看，即Baker在使用“B必胜定理”时，无意中扩大了其适用范围，定理实质上被篡改为了：“如果S是可数集，并且S⊆[0,1]，则B肯定有必胜策略。”如此一来，在S=[0,1]的约定下,并假设[0,1]可数，利用篡改后的“B必胜定理”就可以形式上有效地推出“B有必胜策略”。但是，由于篡改后的“B必胜定理”事实上并不成立，以其为前提的推论也就不可靠，所谓的“矛盾”仍然是假矛盾。

总之，Baker这个反证法证明是无效的，“[0,1]是不可数集”并不是一个可靠的推理结论。

6. 试论实数不可数与戴德金分割不相容

考察区间（0，1），由于其内的有理可数，因此可以用康托尔的方法一一为之编号1，2，3……。现在，我们把编号为1的有理数（假设是0.5）挖去，那么区间（0，1）将被分为两个部分（0，0.5）与（0.5，1），将这两个部分分别编号为0与1；接下来挖去编号为2的有理数，则前面已编号的部分必定有一个又被为两部分，使其中之一保持被分前的编号，而将另外一部分编号为2，接下来挖去编号为3的有理数，则前面已编号的部分必定有一个又被为两部分，使其中之一保持被分前的编号，而将另外一部分编号为3；如此等等，当将所有的有理数挖去后，全部所剩部分的编号分别为0，1，2……恰好是全部自然数，因此全部的所剩部分是可数的。

既然全部有理数已经被挖去，剩下的可数部分当然是包含了全部无理数；然而问题在于，如果戴德金分割是正确的话，我们可以证明这剩下的每一部分最多只能包含单一的无理点！假设存在一个剩余部分包含至少两个不同无理点，那么这两个无理点之间也不可能存在有理点；否则的话，这两个不同的无理点将会因挖有理点的操作而被分开，不可能还同属于一个部分。换句话说，也即在数轴上至少存在两个无理点，而它们之间没有任何有理点。但是如此一来，这样两个不同的无理点所对应的将是同一个戴德金分割，这显然与戴德金分割的唯一性相矛盾。

当然，按照潜无穷观我们是不可能把无穷个有理数挖完的，但是按照康托尔的实无穷观，却是可以挖完的，否则的话，他证明实数不可数的对角线构造法也是不可能完成的——也即他所谓的新数是不可能构造出来的——这也正是潜无穷观者不承认对角线法有效性的根源所在。不过，既然我们是论证康托尔实数不可数的无穷理论与戴德金分割的矛盾，当然要采用他的可以完成的实无穷观，否则无异于鸡同鸭讲，自说自话。

因此，按照可完成的实无穷观，如果有理数可数，并且戴德金分割是正确的，那么无理数同样也是可数的，进而实数也是可数的。反之，如果实数不可数，则：要么康托尔可完成的实无穷观有问题，要么有理数不可数，要么戴德金分割不正确，要么康托尔的对角线法不成立。

当然，以上结论还需要一个隐性假设作为大前提，也即实数只包含有理数与无理数两部分，这两者之外再没有其他的组成部分。如果要否定这个大前提的话，那么结果就只能是扩张实数，走向非标准分析。

7. 结论

除了隐性假设的问题，反证法本质上也并不是完全的演绎推理，因为由矛盾到对假设的否定，其实还应该包含一个因果关系分析，也即必须确定要否定的假设确实是导致矛盾的原因所在。因果关系分析，至少可以追溯到穆勒五法，现在当然是有了很大进步，比如各种统计推断、反事实理论以及朱迪亚·珀尔的因果图等，但它们本质上还是属于归纳推理。尽管如此，反证法还是有必要尝试引入现代因果关系分析技术的一部分，以尽量减少显性假设成为“替罪羊”风险。

参考文献

[1] 文兰.悖论的消解[M].科学出版社，2018.

[2] 莫绍揆.逻辑代数初步[M].江苏人民出版社，1980.

[3] (波兰)塔尔斯基.逻辑与演绎科学方法论导论[M].周礼全,吴允曾,晏成书译.北京:商务印书馆,2011.

[4] 黄展骥.“说谎者悖论 ”、“亦此亦彼悖论 ”的简明消解—— “复合命题 ”和 “矛盾定义”谬误[J].安徽大学学报 (哲学社会科学版),2005(02).

[5] 张光鉴，张铁声.相似论与悖论研究[M].香港天马图书有限公司，2003.

返转到

zmn-000文清慧：发扬啄木鸟精神-《数学啄木鸟专栏》开场白及目录