博文
AFEPack 基础知识
|||
AFEPack是Adaptive Finite Element PACKage的缩写,是由李若教授和刘文斌教授开发的一个自适应有限元软件包,它实际上是一个类库,供有限元处理调用。
1、AFEPack的优势在:
(1)只要能够提供单元的几何信息和基函数,就可建立关于任意类型三角形的有限元空间。
(2)可以处理自适应网格,而且能处理多重网格,它能基于这些不同的网格分别建立有限元空间,并通过建立双线性算子矩阵来联系这些有限元空间。所以这可适用于多个变量或者不同的变量的正则性或者这些变量的不规则区域在不同位置上。
2、AFEPack分为三个层次:
(1)有限单元模块:建立有限元空间的基础,只需用户提供参考单元信息,并指定给网格中的每一个单元。
(2)网格自适应模块:基于遗传树。不同网格必须建立在同一个遗传树上,才能建立网格间关系,即建立基于不同网格的不同有限元空间的双线性算子。
(3)应用模块:用于开发。
3、AFEPack的特点:
(1)建立基于一个网格的一个有限元空间,其中单元具有多样性:(a)单元形状多样,三角形、矩形甚至任何形状;(b)一个有限元空间中可以有多种形状的单元(c)单元可以任意维数(d)完全自动管理自由度 (e)可以自己设定边界条件;
(2)建立基于一个网格的不同有限元空间,其中的关系:(a)建立有限元空间之间的双线性算子矩阵(b)产生从一个有限元空间到另一个的有限元函数(c)离散这个有限元函数;
(3)建立基于一个几何遗传树的不同的自适应网格:(a)在遗传树上获得自适应网格(b)根据一个指示子网格自适应(c)适应一个网格到另一个网格。
(4)建立基于一个几何遗传树的不同的自适应网格的不同有限元空间的关系。
4、AFEPack的使用步骤:
(1)生成并读取网格数据
(2)建立参考单元
参考单元=几何信息(=三角形形状+计算体积的函数+数值积分信息)+坐标转换(映射参考单元和真实单元之间的点)+自由度+基函数
(3)建立有限元空间
有限元空间=网格+参考单元
(4)建立刚度矩阵(每个试函数得到一个方程,形成一个线性代数系统,系数矩阵就是代数矩阵)
(5)求解拉普拉斯方程(已知右端项和边界条件)
(6)网格自适应(引入不规则网格和指示子)
(7)多重网格运算
5、AFEPack的逻辑关系:
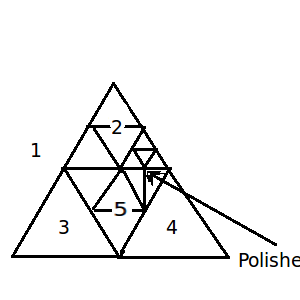
(1)所有网格要产生关系,必须基于同一颗几何遗传树,又称四叉树(一个三角形,加密一次,每个边上取一个中点,就变为四个三角形)。
(2)能够完全覆盖整个网格的子网格组合称为完全子树。多套网格即为不同的完全子树。
(3)通过图中可以看出,网格加密时可能在一条边上出现多个悬点,这时的网格称为irregular mesh
(4)通过semi-regularize,即再加密,使网格一条边上最多只有一个悬点。
(5)通过regularize,使网格变为regular mesh,此时每条边上都没有悬点。方法就是在悬点上加一条线,分割一个三角形成为两个。原来的三角形就有了四个点,成为twin-triangle。
(6)自适应加密时网格上肯定会出现twin-triangle,除非全局均匀加密。故自适应时必须将triangle和twin-triangle的几何信息都读入。
AFEPack中的数据结构
AFEPack中的数据存储是循序渐进的,很有层次。要想获得各个层次的几何信息,需要了解这个包中对于数据结构的定义,这个在定义指示子indicator时尤其重要。
GeometryBM类:几何体的材料标识类。
Geometry类:几何体的序号存储类。类中有两个数组,一个是顶点序号,一个是拓扑边界几何体的序号。
Mesh类:各维几何体的数组存储类。每个几何体用“第n维的第m个几何体”来表述。
假定Mesh类的一个实例化对象是mesh,取出各维几何信息的操作步骤如下:
1、得到k维几何体的个数:u_int n=mesh.n_geometry(k);
2、得到k维下第m个几何体的标识(m大于等于0,小于n):GeometryBM & geo=mesh.geometry(k,m);
3、得到这个几何体的拓扑边界个数:u_int n_bnd=geo.n_boundary();
4、得到k-1维下第i个边界的序号(i大于等于0,小于n_bnd):u_int bnd_index=geo.boundary(i);
5、得到k-1维下这个边界:GeometryBM & bnd_geo=mesh.geometry(k-1,bnd_index);
.......................................
如上一直取下去,直到“0维几何体”,即几何体的顶点,也就是网格的节点。这个0维几何体相对比较特殊:它的顶点序号其实就是它的坐标,它的拓扑边界没有意义,避免使用这个信息,可能会发生未知错误。
6、得到几何体geo的第k个顶点的坐标,步骤如下:
(1)得到第k个节点几何体的序号:u_int vtx_index=geo.vertex(k);
(2)得到这个节点几何体的标识:GeometryBM & vtx_geo=mesh.geometry(0,vtx_index);
(3)得到这个节点几何体坐标的序号:u_int pnt_index=vtx_geo.vertex(0);
(4)得到这个坐标实际值:Point<DOW> & pnt=mesh.point(pnt_index);
库内部不能保证vtx_index和pnt_index一样,但如果自己可以保证两者一样,就可以简化两行代码,变为:
(1)得到第k个顶点坐标的序号:u_int pnt_index=geo.vertex(k);
(2)得到这个坐标实际值:Point<DOW> &pnt=mesh.point(pnt_index);
这个Point型的对象实际就是欧式空间中的一个坐标,如果是三维空间,则它有pnt[0]、pnt[1]和pnt[2]三个double型数值,这样就可以对其进行实际操作。
编程整个流程:
1、建立封装了整个求解过程的problem类。由于类中包括了整个过程,这样类中的所有私有成员变量都可以被类中的成员函数直接调用,无须每个函数中都定义,即成员变量的作用域是整个类。
2、 调用problem类的初始化函数initialize()。这个过程包括:读入网格信息,并首先加密n次;建立几何模板信息;调用构造有限元空间函数 buildFEMSpace(),构造一个有限元空间(这个过程实际包括:将网格和几何信息组装形成有限元空间,并在有限元空间基础上建立有限元函数); 设置初始时间t和时间步长dt。
3、调用problem类的运行函数run()。这是一个循环体,目前终止条件始终为真,每dt运行一次,依次执行以下步骤:执行步进函数stepForward()、执行自适应函数adaptMesh()、累加时间变量、输出有限元函数数据等。
细节内容为:
stepForward()的执行过程:在误差仍大于某值的情况下,作循环(由step变量记录循环次数):(1)建立刚度矩阵 stiff_matrix,这里就是调用继承自StiffMatrix类的自定义的一个Matrix类的实例化对象(2)处理右端项rhs(3)应用边界 条件(4)求解有限元函数(5)计算并判断误差大小。
adaptMesh()的执行过程:(1)创建指示子,并用getInditcator函数获得指示子(2)更新网格:把现有非规则网格的值存储为旧非规 则网格,再动态分配一个新的非规则网格,把现有有限元空间和有限元函数存储为旧的有限元空间和旧有限元函数(3)进行自适应(4)在新的非规则网格的基础 上产生新规则网格,并再次构造有限元空间,注意这次构造之后就会产生新的有限元空间和新的有限元函数。(5)更新有限元函数:将旧有限元函数插值到新有限 元函数上。(6)释放所有旧量的内存空间
4、求解完毕,返回成功信号值:return 0。
二、始终记得类中的私有成员变量可以被成员函数所调用,其作用域遍及整个类。这个在新旧网格的更替中非常重要,既可以保留旧网格、旧空间、旧函数,又可以同时使用新网格、新空间、新函数。
https://blog.sciencenet.cn/blog-441611-608901.html
上一篇:AFEPack 学习注意点
下一篇:编程知识 专贴
1、AFEPack的优势在:
(1)只要能够提供单元的几何信息和基函数,就可建立关于任意类型三角形的有限元空间。
(2)可以处理自适应网格,而且能处理多重网格,它能基于这些不同的网格分别建立有限元空间,并通过建立双线性算子矩阵来联系这些有限元空间。所以这可适用于多个变量或者不同的变量的正则性或者这些变量的不规则区域在不同位置上。
2、AFEPack分为三个层次:
(1)有限单元模块:建立有限元空间的基础,只需用户提供参考单元信息,并指定给网格中的每一个单元。
(2)网格自适应模块:基于遗传树。不同网格必须建立在同一个遗传树上,才能建立网格间关系,即建立基于不同网格的不同有限元空间的双线性算子。
(3)应用模块:用于开发。
3、AFEPack的特点:
(1)建立基于一个网格的一个有限元空间,其中单元具有多样性:(a)单元形状多样,三角形、矩形甚至任何形状;(b)一个有限元空间中可以有多种形状的单元(c)单元可以任意维数(d)完全自动管理自由度 (e)可以自己设定边界条件;
(2)建立基于一个网格的不同有限元空间,其中的关系:(a)建立有限元空间之间的双线性算子矩阵(b)产生从一个有限元空间到另一个的有限元函数(c)离散这个有限元函数;
(3)建立基于一个几何遗传树的不同的自适应网格:(a)在遗传树上获得自适应网格(b)根据一个指示子网格自适应(c)适应一个网格到另一个网格。
(4)建立基于一个几何遗传树的不同的自适应网格的不同有限元空间的关系。
4、AFEPack的使用步骤:
(1)生成并读取网格数据
(2)建立参考单元
参考单元=几何信息(=三角形形状+计算体积的函数+数值积分信息)+坐标转换(映射参考单元和真实单元之间的点)+自由度+基函数
(3)建立有限元空间
有限元空间=网格+参考单元
(4)建立刚度矩阵(每个试函数得到一个方程,形成一个线性代数系统,系数矩阵就是代数矩阵)
(5)求解拉普拉斯方程(已知右端项和边界条件)
(6)网格自适应(引入不规则网格和指示子)
(7)多重网格运算
5、AFEPack的逻辑关系:
(1)所有网格要产生关系,必须基于同一颗几何遗传树,又称四叉树(一个三角形,加密一次,每个边上取一个中点,就变为四个三角形)。
(2)能够完全覆盖整个网格的子网格组合称为完全子树。多套网格即为不同的完全子树。
(3)通过图中可以看出,网格加密时可能在一条边上出现多个悬点,这时的网格称为irregular mesh
(4)通过semi-regularize,即再加密,使网格一条边上最多只有一个悬点。
(5)通过regularize,使网格变为regular mesh,此时每条边上都没有悬点。方法就是在悬点上加一条线,分割一个三角形成为两个。原来的三角形就有了四个点,成为twin-triangle。
(6)自适应加密时网格上肯定会出现twin-triangle,除非全局均匀加密。故自适应时必须将triangle和twin-triangle的几何信息都读入。
AFEPack中的数据结构
AFEPack中的数据存储是循序渐进的,很有层次。要想获得各个层次的几何信息,需要了解这个包中对于数据结构的定义,这个在定义指示子indicator时尤其重要。
GeometryBM类:几何体的材料标识类。
Geometry类:几何体的序号存储类。类中有两个数组,一个是顶点序号,一个是拓扑边界几何体的序号。
Mesh类:各维几何体的数组存储类。每个几何体用“第n维的第m个几何体”来表述。
假定Mesh类的一个实例化对象是mesh,取出各维几何信息的操作步骤如下:
1、得到k维几何体的个数:u_int n=mesh.n_geometry(k);
2、得到k维下第m个几何体的标识(m大于等于0,小于n):GeometryBM & geo=mesh.geometry(k,m);
3、得到这个几何体的拓扑边界个数:u_int n_bnd=geo.n_boundary();
4、得到k-1维下第i个边界的序号(i大于等于0,小于n_bnd):u_int bnd_index=geo.boundary(i);
5、得到k-1维下这个边界:GeometryBM & bnd_geo=mesh.geometry(k-1,bnd_index);
.......................................
如上一直取下去,直到“0维几何体”,即几何体的顶点,也就是网格的节点。这个0维几何体相对比较特殊:它的顶点序号其实就是它的坐标,它的拓扑边界没有意义,避免使用这个信息,可能会发生未知错误。
6、得到几何体geo的第k个顶点的坐标,步骤如下:
(1)得到第k个节点几何体的序号:u_int vtx_index=geo.vertex(k);
(2)得到这个节点几何体的标识:GeometryBM & vtx_geo=mesh.geometry(0,vtx_index);
(3)得到这个节点几何体坐标的序号:u_int pnt_index=vtx_geo.vertex(0);
(4)得到这个坐标实际值:Point<DOW> & pnt=mesh.point(pnt_index);
库内部不能保证vtx_index和pnt_index一样,但如果自己可以保证两者一样,就可以简化两行代码,变为:
(1)得到第k个顶点坐标的序号:u_int pnt_index=geo.vertex(k);
(2)得到这个坐标实际值:Point<DOW> &pnt=mesh.point(pnt_index);
这个Point型的对象实际就是欧式空间中的一个坐标,如果是三维空间,则它有pnt[0]、pnt[1]和pnt[2]三个double型数值,这样就可以对其进行实际操作。
编程整个流程:
1、建立封装了整个求解过程的problem类。由于类中包括了整个过程,这样类中的所有私有成员变量都可以被类中的成员函数直接调用,无须每个函数中都定义,即成员变量的作用域是整个类。
2、 调用problem类的初始化函数initialize()。这个过程包括:读入网格信息,并首先加密n次;建立几何模板信息;调用构造有限元空间函数 buildFEMSpace(),构造一个有限元空间(这个过程实际包括:将网格和几何信息组装形成有限元空间,并在有限元空间基础上建立有限元函数); 设置初始时间t和时间步长dt。
3、调用problem类的运行函数run()。这是一个循环体,目前终止条件始终为真,每dt运行一次,依次执行以下步骤:执行步进函数stepForward()、执行自适应函数adaptMesh()、累加时间变量、输出有限元函数数据等。
细节内容为:
stepForward()的执行过程:在误差仍大于某值的情况下,作循环(由step变量记录循环次数):(1)建立刚度矩阵 stiff_matrix,这里就是调用继承自StiffMatrix类的自定义的一个Matrix类的实例化对象(2)处理右端项rhs(3)应用边界 条件(4)求解有限元函数(5)计算并判断误差大小。
adaptMesh()的执行过程:(1)创建指示子,并用getInditcator函数获得指示子(2)更新网格:把现有非规则网格的值存储为旧非规 则网格,再动态分配一个新的非规则网格,把现有有限元空间和有限元函数存储为旧的有限元空间和旧有限元函数(3)进行自适应(4)在新的非规则网格的基础 上产生新规则网格,并再次构造有限元空间,注意这次构造之后就会产生新的有限元空间和新的有限元函数。(5)更新有限元函数:将旧有限元函数插值到新有限 元函数上。(6)释放所有旧量的内存空间
4、求解完毕,返回成功信号值:return 0。
二、始终记得类中的私有成员变量可以被成员函数所调用,其作用域遍及整个类。这个在新旧网格的更替中非常重要,既可以保留旧网格、旧空间、旧函数,又可以同时使用新网格、新空间、新函数。
https://blog.sciencenet.cn/blog-441611-608901.html
上一篇:AFEPack 学习注意点
下一篇:编程知识 专贴