博文
科斯塔斯阵列,有限域,声纳和最难听的音乐
 精选
精选
|||
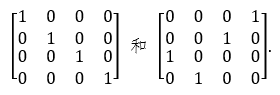
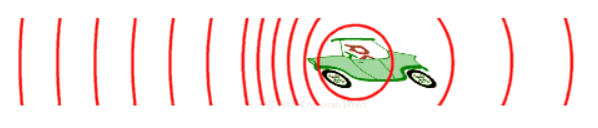
作者:蒋迅 本文发表在《中国工业与应用数学学会通讯》2019年第3期。 从游斯彬的文章,我们看到了陈奕迅把歌唱到了最难听的境地。陈奕迅能做到这一点真的是不容易。但对数学家来说,创作出一个最难听的歌曲并不是特别难的事情。今天我就来讲讲数学家是怎样做到的。不过先要从一个看似无关的数学游戏说起。由此我们介绍数学在通讯科学中的一个应用,然后以最难听的音乐结束本文。 建议在阅读这一篇之前,先阅读笔者对哥隆尺的介绍。这样可能对本文的思想有些帮助。不过,本文并不要求读者具有哥隆尺的知识。 1. 科斯塔斯阵列的定义 我们考虑在平面上的 n×n 的网格。在这些网格中,我们将放入n个圆点,使得在每一行和每一列上都只有一个圆点。我们可以用 0 和 1 来代替这些点:有圆点的方格上我们放入 1,否则就放入 0。满足上述描述的最简单的网格就是对角网格。下面是两个 再看一个非对角网格。 使用0和1表示的的好处是便於文字叙述。我们可以把一个 n×n 的网格看成是一个矩阵(或者称为阵列):从左到右分别为第 1, 2, …, n 列;从上到下分别为第 1, 2, …, n 行。在第 i 行第 j 列的数字就可以用 ai,j 或 a(i,j) 来表示,即 ai,j = 1 如果相应的格子里是1,否则 ai,j = 0。注意,我们在这里是从上往下为递增方向,因为这个表示法与数学上的矩阵的一般表达是一致的: 我们希望使用这种矩阵的表达形式,但我们并不要求读者有矩阵的知识。所以我们情愿把它叫作阵列。 对於上面的对角网格来说,四个圆点的坐标是: (1,1), (2,2), (3,3), (4,4);另一个非对角的网格的圆点坐标则是 (3,1), (4,2), (2,3), (1,4)。用矩阵的表示法,上面两个例子分别是 作为交换矩阵,我们也可以把它写成数学上的“排列”。比如上面的对角矩阵可以写成一个平凡排列:[1,2,3,4];非对角矩阵可以写成 [3,4,2,1],它是平凡排列 [1,2,3,4] 的一个排列。像我们介绍的哥隆尺,我们可以从排列的表示来构造倒三角。当初科斯塔斯就是从这个角度来构造最初的几个科斯塔斯阵列的。我们不深入讨论。 我们现在可以给出科斯塔斯阵列的定义了。数学上,科斯塔斯阵列首先是在平面上的满足上述条件的 n×n 的网格上的 n 个点。每两个圆点的连线形成一个线段。我们也可以把它们看作是向量,只是没有一个明确的方向。这样的向量一共有 在上面的两个例子中,第一个对角阵列显然不是一个科斯塔斯阵列,比如 (1,1) 和 (2,2) 形成的向量和由 (2,2) 和 (3,3) 形成的向量的方向和长度是一样的,它们都是与水平线构成45度角且长度为 √2 的线段。第二个非对角阵列是一个科斯塔斯阵列。读者可以找出它的全部 如果我们把这里的网格比作刻度尺的话,那么科斯塔斯阵列就可以比作哥隆尺。所以我们可以把科斯塔斯阵列看作是哥隆尺在二维的推广。 2. 科斯塔斯阵列的一个等价定义 科斯塔斯阵列有一个等价的定义,而这个定义能帮助我们理解科斯塔斯阵列在应用中的意义。为此,我们对阵列 A 扩展如下: 也就是将阵列 A 往四个方向用 0 无限延伸。我们称之为 A 的扩展阵列。我们定义阵列A 的非周期自相关函数(autocorrelation function)为 对扩展阵列 A' = (ai,j),我们把一个阵列向右移动 u 单位,同时向下移动 v 单位,得到的是 A'u,v = (ai+v,j+u). 显然,CA 就是把阵列 A' 和它的 (u,v) 平移阵列 A'u,v 在它们的相同坐标上的值两两相乘,然后相加这些乘积。这个数越大,那么它的自相关就越高。如果 (u,v) = (0,0),那么 A' 与 A'u,v CA(u,v) = n. 注意到当 |u| ≥ n 或 |v| ≥ n 时,A'u,v 已经移到 A' 可能取1的范围之外,因而这时必有 CA(u,v) = 0. 所以我们只需考虑 |u| < n 或 |v| < n 的情况。也就是说,我们可以把 CA 看作是一个 (2n - 1)×(2n - 1) 的阵列。回到我们前面的一个对角阵列和非对角阵列的例子上,为说话方便,我们把它们分别记为 A 和 B。这时,n = 4. 经简单计算,我们可以得到下面两个 7×7 阵列: 注意坐标 (0,0) 在这两个阵列的中心,而且在坐标 (0,0) 上的值都是4。比较两个例子,我们还可以看到,CA 中对角线上的值是逐渐递减的,而 CB 上除了在中心有一个4以外,其他的值都是0和1。事实上,我们可以证明满足这个性质的置换阵列就一定是科斯塔斯阵列,反之亦然。容易看出,当 n 充分大时,科斯塔斯阵列只有在原点 (0,0) 的自相关函数值达到 n。对其他平移后的点,其自相关函数值都非常小;而对角阵列则不具备这个性质。 在本节的最后,我们顺便定义两个 n×/n 阵列 A 和 B 的互相关函数(cross-correlation function): 3. 科斯塔斯和已知的一些科斯塔斯阵列 约翰·科斯塔斯(John P. Costas)是美国电子工程师。1947年,他从普渡大学毕业。这时正值第二次世界大战。他加入了美国海军,成了一名雷达军官。后来他进入麻省理工学院,研究干扰滤波和线性系统编码。在学校里,他得到了美国应用数学家诺伯特·维纳(Norbert Wiener)、义裔美籍计算机科学家罗伯特·法诺(Robert Mario Fano)、美国电子工程学家杰罗姆·威斯纳(Jerome Bert Wiesner)和中国现代早期电机工程学家李郁荣。从1951年开始,他受用于通用电气公司。1980年代初,他转到Cogent Systems公司直到退休。科斯塔斯最著名的成就还不是科斯塔斯阵列,而是他在1950年代发明的对现代数字通信产生深远影响的后循环(Costas loop)。进入1960年代后,他解决了声纳系统效果不佳的问题。他的解就是本文的科斯塔斯阵列。我们将在稍后做详细介绍。 找到科斯塔斯阵列比找到哥隆尺相对容易一些,因为在二维上自由度比一维大一些。科斯塔斯在1975年用手在一张纸上凑出了一个 12×12 的科斯塔斯阵列。由於他无法找到更大的例子,他怀疑对 n > 12 可能不存在这样的阵列。但后来人们发现了一些算法,可以得到任意大的科斯塔斯阵列。下面的表格给出前36阶的科斯塔斯阵列的数量表。 目前,从 n = 1 到29的所有科斯塔斯阵列都已经找到。在29之后还没有一个 n 得到了全部科斯塔斯阵列。我们用斜体字表示我们得到的是科斯塔斯阵列的数目的下限。特别让人们意外的是,至今人们还没有找到 n = 32 和 33 时哪怕一个科斯塔斯阵列。人们也无法证明不存在 n = 32 和 33 时的科斯塔斯阵列。甚至有人估算说,当 n = 32 时,用现在已知的算法和现有的设备,找到全部科斯塔斯阵列需要45000年的计算机时间!所以至今是否对任意的正整数 n 来说都存在科斯塔斯阵列还是一个未解之谜。人们仍然在努力寻找新的算法。我们不打算囊括全部这些算法,而只是介绍一下最早的两个算法。这两个构造法都有很强的数学背景。 4. 有限域和原根 这里我们要说到的数学背景有一段悲催的故事。这个故事始于200年前的法国。一位年轻人伽罗瓦(Evariste Galois)为了解决困扰五次多项式的根式解问题另辟奇径,搞出来一个所有当时的大数学家都无法理解的思路。政治上,他强烈支持共和,受到保皇势力的打压。更奇特的是,在他21岁的时候为一位女子与人决斗。决斗前,他匆忙写下了他的数学成果,然后委托他的朋友务必找到出版的地方。他的稿子没有得到高斯(Johann Karl Friedrich Gauss)、雅可比(Carl Gustav Jacob Jacobi)的赏识。所幸的是,这个稿子后来被刘维尔(Joseph Liouville)的肯定,终於发展成为了数学界的丰碑“伽罗瓦理论”。他的故事已经出现许多数学科普作品中。我们后面会看到卡斯塔斯阵列在通讯中的应用。估计伽罗瓦没有想到的是,他的数学成果能在二百多年后应用到通讯领域。 在数学上,实数的全体构成一个“域”。所谓域,就是一个代数结构,在它里面可以进行加、减、乘和除(除数不为零)运算。比如说两个实数相加还是实数,两个实数相除也还是实数,只要除数不是零。运算结果仍然保留在这个代数结构里。我们看到,域的概念是数域以及四则运算的推广。 实数域是一个无限域。但并不是所有的域都是无限的。有限域也被称为伽罗瓦域(Galois field),很显然是为了纪念这位伟大的法国数学家伽罗瓦。有限域就是具有加减乘除运算的包含有限个元素的域。有限域最常见的例子是当 p 为素数时,整数对 p 取模。我们把它记为 GF(p)。它的元素可以用 0, …, p - 1 表示。我们假定对这些元素做四则运算时在取模的意义下进行。也就是说,一旦一个运算结果达到了 p,就将这个数归零;运算结果超过了 p 时就把这个数减去 p,直到其结果落入到 0 到 p - 1 的范围之内。这种运算叫作模运算(mod),一般用“≡”表示,但是在代数学里也会用“=”表示,只要不会引起混淆。以 GF(7) 为例,它的元素为 0, …, 6。我们有 1 + 4 ≡ 5 (mod 7) ,4 + 5 = 9 ≡ 2 (mod 7)。有了模运算后,我们就可以引入欧拉函数的概念。定义欧拉函数 φ(p) 为与 p 互素并小於或等於 p 的那些正整数的个数。在我们考虑的例子中,p 为素数,所以总是有 φ(p) = p - 1。注意欧拉函数并不只是对素数定义的。在后面的科斯塔斯阵列的算法中也会用到更一般的整数的欧拉函数。 我们还需要引入数论中原根的概念。对於两个互素的正整数 g 和 p,数论中有欧拉定理保证了,必存在正整数 d ≤ p - 1,使得 gd ≡ 1 (mod p)。我们不妨假设 d 是满足上述条件中的最小的那个正整数。如果这个 d 满足 φ(p) = d,那么基数 g 叫作模 p 的原根。我们以 p = 7 为例,显然有 φ(p) = 6。我们说 g = 3 是一个原根,因为 而当基数为2时,23 = 8 ≡ 1 (mod 7),但是指数 3 < 6 = φ(p)。从而2不是模7的一个原根。我们看到,3k 模7的周期为6。在这个周期里,模7后的余数是 3, 2, 6, 4, 5, 1。这正好是 1, 2, 3, 4, 5, 6 的一个置换。这样做出的置换是一个科斯塔斯阵列。 现在我们可以介绍科斯塔斯阵列的构造法了。至今科斯塔斯阵列的构造法仍然是一个活跃的科研领域。但限於篇幅,我们只介绍两个最早出现的方法:卫曲构造法和蓝波-哥伦布构造法。 5. 劳埃德·卫曲和卫曲构造法 卫曲阵列是最早的一个构造方法。其实,这个方法是由美国数学家和编码专家埃德加·吉尔伯特(Edgar Gilbert)在1965年,即科斯塔斯发现科斯塔斯阵列的同时发现的。当然这个时候他并不知道科斯塔斯的工作。所以他的出发点是不同的:拉丁方阵(Latin square)。可惜的是,科斯塔斯发现了科斯塔斯阵列但是没有开发一套计算方法,而吉尔伯特设计了一个巧妙的方法却不知道科斯塔斯阵列。由於他们两人没有出现交集而使得吉尔伯特的工作被埋没了。一直到1982年,吉尔伯特的构造法才重新被美国应用数学家和信息科学家劳埃德·卫曲(Lloyd R. Welch)发现。 卫曲于1951年毕业于伊利诺伊大学厄巴纳-香槟分校数学系,又在1958年从加州理工学院获得数学博士学位。他的博士论文的题目是:摼砘值呐判蚝妥畲蠡瘮。比较自相关函数和卷积,我们可以感觉到他在读书的时候就已经为他以后的工作铺垫了道路。毕业后他在喷气推进实验室、国防分析研究所和南加州大学工作。卫曲的主要贡献是寻找隐马尔可夫模型的未知参数的鲍姆-卫曲算法(Baum─Welch algorithm)和一种用于高效地解码BCH码与里德-所罗门码的伯利坎普-卫曲算法(Berlekamp-Welch algorithm)。 卫曲并没有投入到科斯塔斯阵列的研究。原来科斯塔斯在用纸笔反复凑答案失败之后,他转向哥伦布求救。这是1970年代后期的事情。哥伦布一方面告诉科斯塔斯,这个问题以前还没有人研究过(其实他是不知道吉尔伯特的工作);他同时向他在南加州大学的同事和合作者卫曲询问。这两个人早就在算法学上长期合作。早在1968年,他们就共同提出了在编码理论里至今未解决的“哥伦布-卫曲”猜想,而且这方面的工作就与伽罗瓦域紧密相关。卫曲意识到了科斯塔斯的问题可以用伽罗瓦域的结果来做。这就是卫曲构造法。1982年,哥伦布在和赫伯特·泰勒合写的一篇关于科斯塔斯阵列的评述中首次介绍了这个算法。随后哥伦布给出了严格的证明。 卫曲构造法:设 p 是一个素数,g 是其原根。令 A = [ai,j] 为一个 p - 1 阶的置换阵列(矩阵),满足下列条件: 上面我们举了一个 p = 7 例子。我们已经看到 GF(7) 的原根 g = 3,而且我们得到了一个由模余数形成的置换 3, 2, 6, 4, 5, 1。可以验证相应的 6 阶阵列 A 就是: 这个科斯塔斯阵列就是一个用卫曲构造法生成的。我们可以把它记作 [1 3 2 6 4 5]。细心的读者会注意到,这个阵列不是想象中的 [3 2 6 4 5 1]。其实,卫曲构造法还可以稍微推广一点。假定 c 是一个整数。令 A = [ai,j] 为一个 p - 1 阶的阵列(矩阵),满足下列条件: 显然,前面的定义是当 c = 0 时的特例。如果c = 1,那么可以看到 而这正是我们预期的阵列 [3 2 6 4 5 1]。这两阵列的区别仅仅是在水平方向的一个平移。所以从本质上说它们是等价的。 6. 蓝波-哥伦布构造法 第二个早期科斯塔斯阵列构造法也是从有限域出发的。这就是哥伦布介绍的蓝波-哥伦布构造法(Lempel-Golomb construction)。 亚伯拉罕·蓝波(Abraham Lempel)出生于波兰。他分别于1963年、1965年和1967年从以色列理工学院获得学士、硕士和博士学位。然后,他作为研究助理前往南加州大学。在那里开始了与哥伦布的长期合作。1969年,他加入了位於马萨诸塞州萨德伯里的斯佩里兰德研究中心任研究员。1971年,他回到以色列理工学院,在那里担任计算机科学教授直到退休。他同时还担任IBM沃森研究中心的职务。他最著名的工作是在无损数据压缩算法的两个算法“LZ77与LZ78”,而且这个工作也是基於有限域的性质。在那段时间里,他在有限域方面有许多研究。顺便提一句,另有一位叫作泰瑞·卫曲(Terry Welch)的美国计算机学家把无损数据压缩算法做了改进,这个新算法称为“蓝波-立夫-卫曲(Lempel-Ziv-Welch)编码法”。 蓝波的算法也是哥伦布与泰勒1982年的同一篇论文中首先披露的。稍后哥伦布完成了证明。哥伦布和泰勒介绍的是一个推广了的蓝波构造法。我们在这里也先介绍蓝波-哥伦布构造法,然后作为一个特例给出蓝波构造法。 蓝波-哥伦布构造法:设 p 为一个素数,n 为一个正整数,q = pn > 2 为 p 的一个幂。再设 φ 和 ρ 为有限域 GF(q) 的两个(可能相同的)原根。令 A = [ai,j] 为一个 q - 2 阶的置换阵列(矩阵),满足下列条件: 当 φ = ρ 时就是蓝波提出的原始情形。 让我们看一个例子:令 p = 11, n = 1,从而 q = pn = 11。计算可知 φ = 2,ρ = 7 是 GF(11) 的两个原根: 於是,使用蓝波-哥伦布构造法,我们可以得到下面的置换阵列: 我们把计算留给读者。 7. 科斯塔斯阵列在声纳的应用 前面我们说过,科斯塔斯是在研究声纳时发现的科斯塔斯阵列的。现在我们就来谈谈声纳与科斯塔斯阵列的关系。 故事还是从科斯塔斯开始。从麻省理工大学博士毕业后,他受命为海军解决用声纳侦查潜艇效率不高的问题。由於电磁波在水中衰减的速率非常的高,无法做为侦测的讯号来源,以声波探测水面下的人造物体成为运用最广泛的手段。无论是潜艇或者是水面船只,都利用这项技术的衍生系统,探测水底下的物体,或者是以其作为导航的依据。声纳的工作原理是它发出音响讯号,借由这个讯号接触物体后反射回来声波的变化,做为计算这个物体的相对方位与距离的资料。这种方法就是利用了多普勒效应。 多普勒效应(Doppler effect)是波源和观察者有相对运动时,观察者接受到波的频率与波源发出的频率并不相同的现象。可能你早就注意到,远方急驶过来的火车鸣笛声变得尖细(即频率变高,波长变短),而离我们而去的火车鸣笛声变得低沉(即频率变低,波长变长)。这就是多普勒效应的现象。这一现象最初是由奥地利物理学家多普勒(Christian Doppler)1842年发现的。 在实际应用中,人们一般是在连续的几个相同的时间段里发出不同频率的声波系列,然后收集反射回来的声波。当收到的一个从移动物体反射回来的回音时,这个系统会与它发出的音频系列各个时间和频率上的平移做比较,从中找到与这个反射回来的信号高度吻合的那个时间和频率的平移。从时间的平移人们可以计算出物体的距离范围;从频率的变化,人们可以计算出物体移动的速度。 这个系列可以用 n×n 的置换阵列 [asub>i,j] 来表示,其中j对应于时间区间 t1, t2, …, tn,i 对应于频率 f1, f2, …, fn,满足:ai,j = 1 当且仅当频率 fi 在时间段 tj 里发射。当这个设定好的频率系列发出去后,接收器稍后收到一组回音。这组回音的频率会因物体的运动速度而有些变化;而发射时间与接受时间之间的时间差则决定于发射器与反射回音的物体之间的距离。 如果没有任何杂音的话,这个结果应该就很好了。但在实际应用中杂音是避免不了的。所以我们必须能够区分背景杂音和目标物体反射的回音。为此,我们必须将收到的信号与发射信号的所有 (2n - 1)(2n - 1) 个组合一一比较,并希望在这些组合中只有那个对应于目标物体的位置和速度的平移与其有较高的互相关性。因此,在设计这组频率信号时,我们必须让我们置换阵列使得其所有的非平凡位移(即零位移)都与其本身具有低相关性。 我们希望以上的讨论已经把科斯塔斯的思想展现出来了。科斯塔斯阵列在通讯上的研究至今活跃,在中国也是同样。我们不打算更深入地从电子工程的角度谈科斯塔斯阵列是如何实施的。但是想指出中国学者在这方面也有一些工作。我们在参考文献里引用了几篇,比如周彦鹏和景晓军对FH-OFDMA 通信系统的简介。 8. 最难听的音乐 现在让我们回到文章开头最难听的音乐。我不知道陈奕迅是如果即兴创作出一首那么难听的音乐,但我猜测他的目标是打破观众的常规期待 ─ 优美的乐曲。那么什么是优美的音乐呢?我想重复是一个关键。毕达哥拉斯早在2500年前就发现音调之间的比例。一首乐曲有旋律,有主题。通过旋律和主题的重复。比如在贝多芬的第五交响曲中的著名的摯锬赡饶葦主题在交响乐中仅在第一乐章里就有数百次。所以这种重复的设置对於美丽来说非常重要。那么,如果我们能创作出一段没有任何重复的音乐,没有旋律,没有模式,没有比例。那么得到的就是一首非常难听的音乐。 这个思想其实早在20世纪30-50年代开始就有人尝试过。著名的奥地利裔美国作曲家和音乐理论家阿诺德·勋伯格(Arnold Schoenberg,1874-1951)提出“解放不和谐”的思想,希望能从音调结构中释放音乐。可惜他在科斯塔斯解决了如何在数学上创造这些结构的问题之前10年就去世了。 经过了上面对科斯塔斯阵列的讨论,我们应该不难想到切入点就是科斯塔斯阵列。钢琴上有88个键,从最左边的低音A(啦)到最右边的高音C(哆)。我们可以把科斯塔斯在声纳中的频率换成钢琴的琴键。正好 p = 89 是一个素数。上面的讨论让我们知道可以构造一个(p - 1)×(p - 1) = 88×88的科斯塔斯阵列。又 g = 3 是 GF(89) 的一个原根。所以我们可以运用卫曲构造法来做。简单计算得到: 从这个计算,我们得到下面的科斯塔斯阵列: 把它换成乐谱就是世界上首个无模式钢琴奏鸣曲(Costas Golomb No. 1: The Perfect Ping): 在这个曲子中,88个琴键的每一个都只弹奏一次,并且是按上述科斯塔斯阵列的顺序。 这段音乐是美国数学家、爱尔兰都柏林大学学院工学院高级讲师斯科特·里卡德(Scott Rickard)为我们创作的。里卡德在麻省理工学院获得数学和计算机与工程学的两个本科学位(1992年和1993年)和电子工程和计算机科学的硕士学位,又在普林斯顿大学获得应用数学和计算数学的硕士和博士学位(2000年和2003年)。他在2011年的TED大会上介绍了这首乐曲。如果你能看到他的演讲视频,那么就可以欣赏由新世界交响乐团室内音乐系主任迈克尔·林维(Michael Linville)演奏的钢琴独奏。我不知道读者会怎样比较陈奕迅和林维的表演,但我们知道林维演奏的乐曲只有数学家可以创作出来。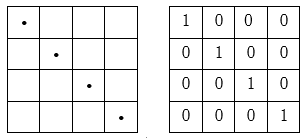
表1
表2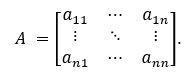
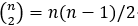 个。当 n = 4 时,容易看出这样的线段一共有 6 个。科斯塔斯阵列就是要求那些向量都不相同(不平行或者不同长度)。
个。当 n = 4 时,容易看出这样的线段一共有 6 个。科斯塔斯阵列就是要求那些向量都不相同(不平行或者不同长度)。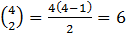 个向量并验证它们都是不同的。
个向量并验证它们都是不同的。
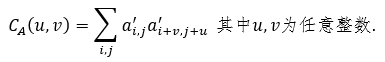
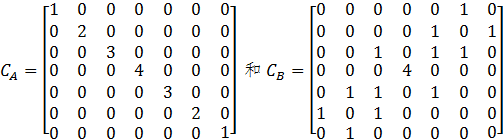
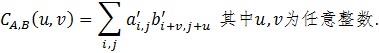

图1. 约翰·科斯塔斯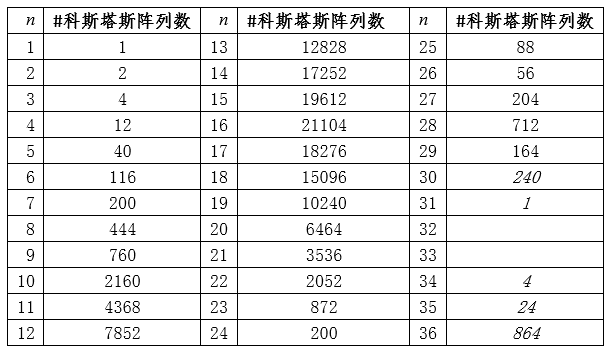
表3. 科斯塔斯阵列一览表

图2. 劳埃德·卫曲

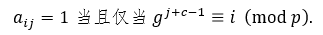





表4
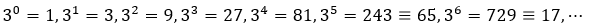

https://blog.sciencenet.cn/blog-420554-1199513.html
上一篇:一把数学的尺子 ─ 哥隆尺
下一篇:【数学应知道】误差简介