科学研究从发现问题开始。爱因斯坦指出：“提出一个问题往往比解决一个问题更重要。因为解决一个问题也许仅仅是一个数学上或实验上的技能而已，而提出新的问题、新的可能性，从新的角度去看旧的问题，都需要有创造性的想象力，而且标志着科学的真正的进步。”

丘成桐教授在评价中国数学的现状时说：近40年来，中国的数学发展很快，但还是不满意，最大的问题是人们解决问题，不是自己提出问题。

《微积分》是研究现实世界确定性运动现象及规律的数学理论，《随机过程》是研究现实世界随机性运动现象及规律的数学理论。《微积分》在发展初期由于出现违反同一律的“贝克莱悖论”，引发了一场持续150多年的数学危机。《随机过程》布朗运动理论出现了图1所示的八个反常问题，也将引发一场数学危机和范式变革。

图1 《随机过程》布朗运动理论中的八个反常问题

下面详细介绍并分析布朗运动理论中的这八个反常问题。

一、与经验事实不符

1、位移正态分布假设与实验结果不符

《随机过程》教科书在布朗运动定义中给出了“布朗运动位移服从（0，σ² t）正态分布”的基本假设：

x(t)～N(0，σ² t)

图2给出了一个布朗粒子的位移观测曲线、位移统计分析结果（直方图）和《随机过程》布朗运动定义假设的正态分布曲线。

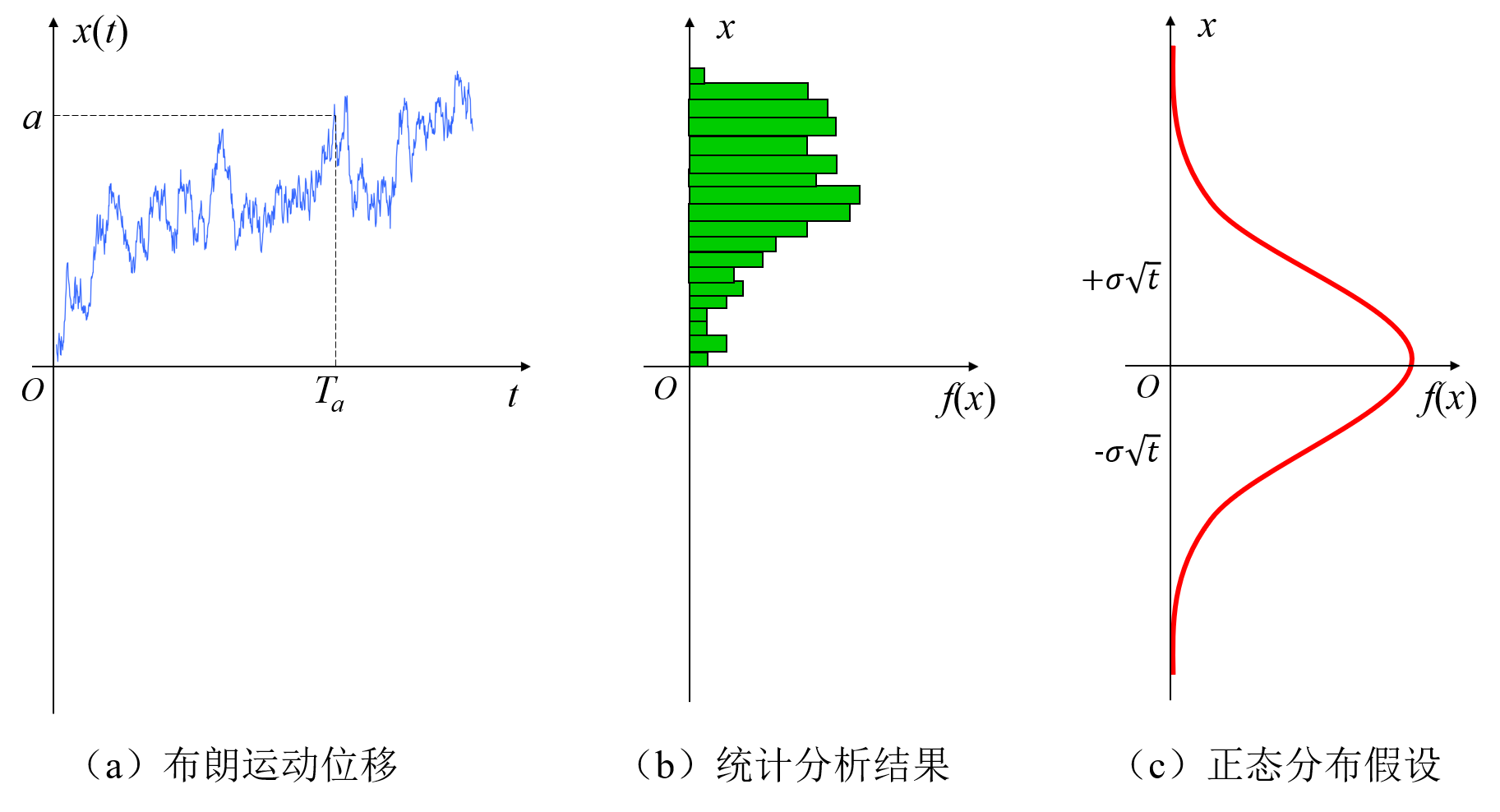
图2 布朗粒子位移观测曲线及统计分析结果

图1（c）所示的正态分布曲线具有如下两个重要的特征：

（1）对称性。绝对值相等的正、负位移出现的次数大致相等。

（2）集中性。绝对值小的位移比绝对值大的位移出现的次数多。

但是，对布朗粒子位移观测曲线的统计分析结果表明：图1（a）的布朗粒子位移观测值均大于零，不存在正态分布的对称性；而且绝大部分位移观测值远离原点，也不具有正态分布的集中性，因此，“布朗运动位移服从正态分布”的基本假设与实验结果不符。

2、瞬时速度无穷大与实验结果不符

《随机过程》教科书从“布朗运动位移服从（0，σ² t）正态分布”的基本假设出发，推导出了“布朗运动瞬时速度无穷大（不存在）”和“布朗运动路径处处不可导”的结论。

布朗运动是一种广泛存在于自然界和人类社会实践活动中的随机运动。自然科学、工程技术和社会科学等领域的观察和实验结果表明：布朗粒子的无规则运动、陀螺随机游走、表面微观轮廓和股票价格波动等不同形式布朗运动的瞬时速度均为平均功率有限的白噪声（图3），布朗运动的瞬时速度（导数）不仅存在，而且可观测。

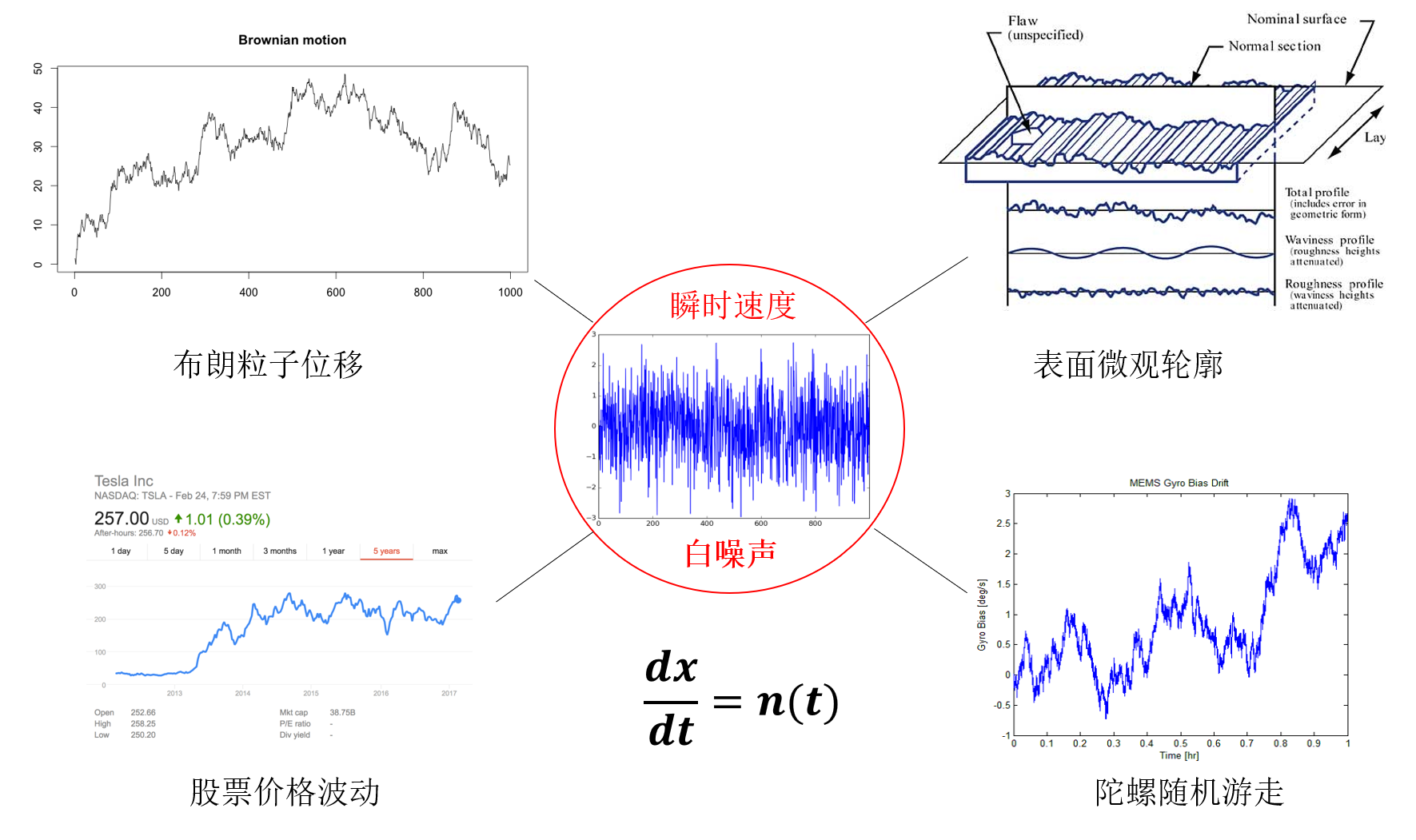
图3 不同形式布朗运动的瞬时速度

 二、逻辑上不能自洽

1、常返性逻辑悖论

布朗运动的常返性是指时间t充分大时，从原点出发的布朗粒子返回原点无穷多次的概率等于1，即

P[x(t)=0，i.o.]=1

布朗粒子返回原点时x(t)=0，根据《概率论》常数的方差等于零性质，有

P[D[x(t)]=0，i.o.]=1

即在t充分大时，D[x(t)]=0发生无穷多次的概率也等于1。

根据x(t)～N(0，σ² t)的基本假设，x(t)的方差为

D[X(t)]=σ² t≠0，t >0时

显然，从布朗运动常返性得出的方差与布朗运动定义给出的方差相互矛盾。

2、首中时逻辑悖论

设T_a为布朗运动首中时（布朗粒子首次到达图1中a位置的时间），则首中位置x(T_a)= a为常数。

根据x(t)～N(0，σ² t)的布朗运动基本假设，可得x(T_a) 的数学期望和方差

E[x(T_a)]=0

D[x(T_a)]= σ²T_a

根据首中位置x(T_a)= a，也可直接计算出x(T_a)的数学期望和方差

E[x(T_a)]= E[a]= a

D[x(T_a)]= D[a]=0

显然，与布朗运动基本假设x(t)～N(0，σ² t)给出的数学期望和方差矛盾。

3、布朗运动定义中的逻辑悖论

设x(t)为一个布朗粒子在t时刻的位移（图1），x(0)=0，定义

（1）x(t)为平稳独立增量过程；

（2）x(t)～N(0，σ² t)，其中σ>0为常数；

（3）x(t)是t的连续函数。

则称x(t)是参数为σ²的布朗运动，或维纳过程。

上述布朗运动定义中隐含了一个与“贝克莱悖论”类似、违反形式逻辑同一律的逻辑错误，用随机变量和时间函数这两个内涵与外延完全不同的数学概念来描述同一个布朗粒子在t时刻的位移x(t)，导致计算出不同的数学期望和方差（图4），因此出现了逻辑悖论。

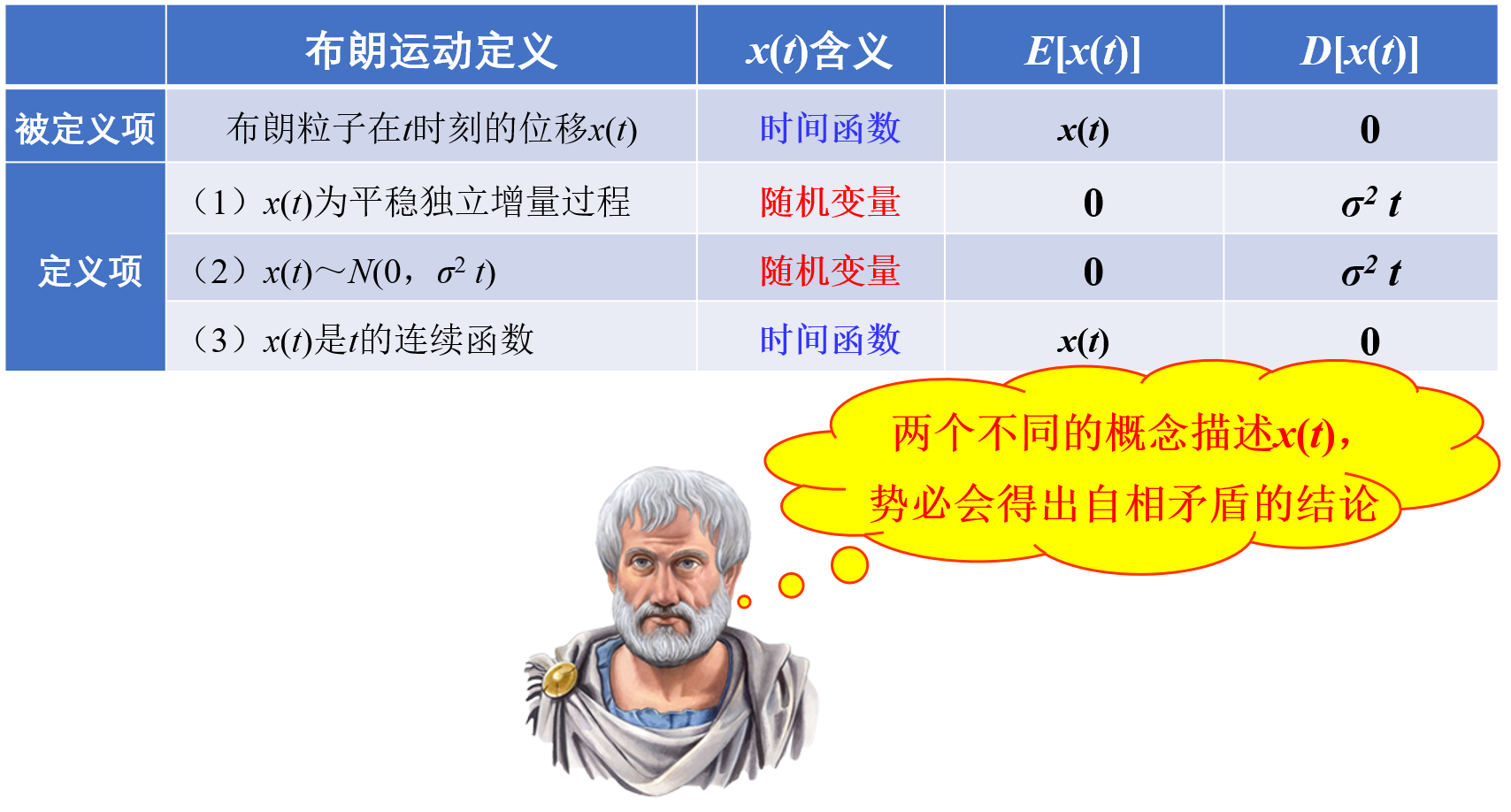
图4 布朗运动定义中的逻辑悖论

三、与基本常识不符

1、混淆浓度和位移基本概念

1905年，爱因斯坦首先对布朗运动进行了定量研究，建立了布朗运动扩散方程，得出了布朗运动的浓度f(x,t)服从正态分布的结论：

f(x,t)～N(0，σ² t)

《随机过程》教科书假设一个布朗粒子在t时刻的位移x(t)也服从与浓度f(x,t)相同的正态分布，给出了如下的布朗运动基本假设：

x(t)～N(0，σ² t)

显然，《随机过程》教科书混淆了浓度与位移基本概念，将描述大量布朗粒子的浓度分布规律当作单个布朗粒子的位移变化规律，这就如同用温度来度量一个分子的动能一样违背基本常识，导致布朗运动基本假设中的数量关系与客观事实不符，使《随机过程》布朗运动理论的客观真理性和逻辑完备性在逻辑出发点就遭到彻底破坏，从而得出了“布朗粒子位移服从正态分布”和“布朗粒子瞬时速度无穷大”等与物理学实验结果不符的错误结论。

2、混淆样本函数和随机变量基本概念

《随机过程》教科书将随机过程试验的所有可能结果映射到样本空间Ω，然后用二元函数X(ω,t)来描述随机过程试验结果（图5）。

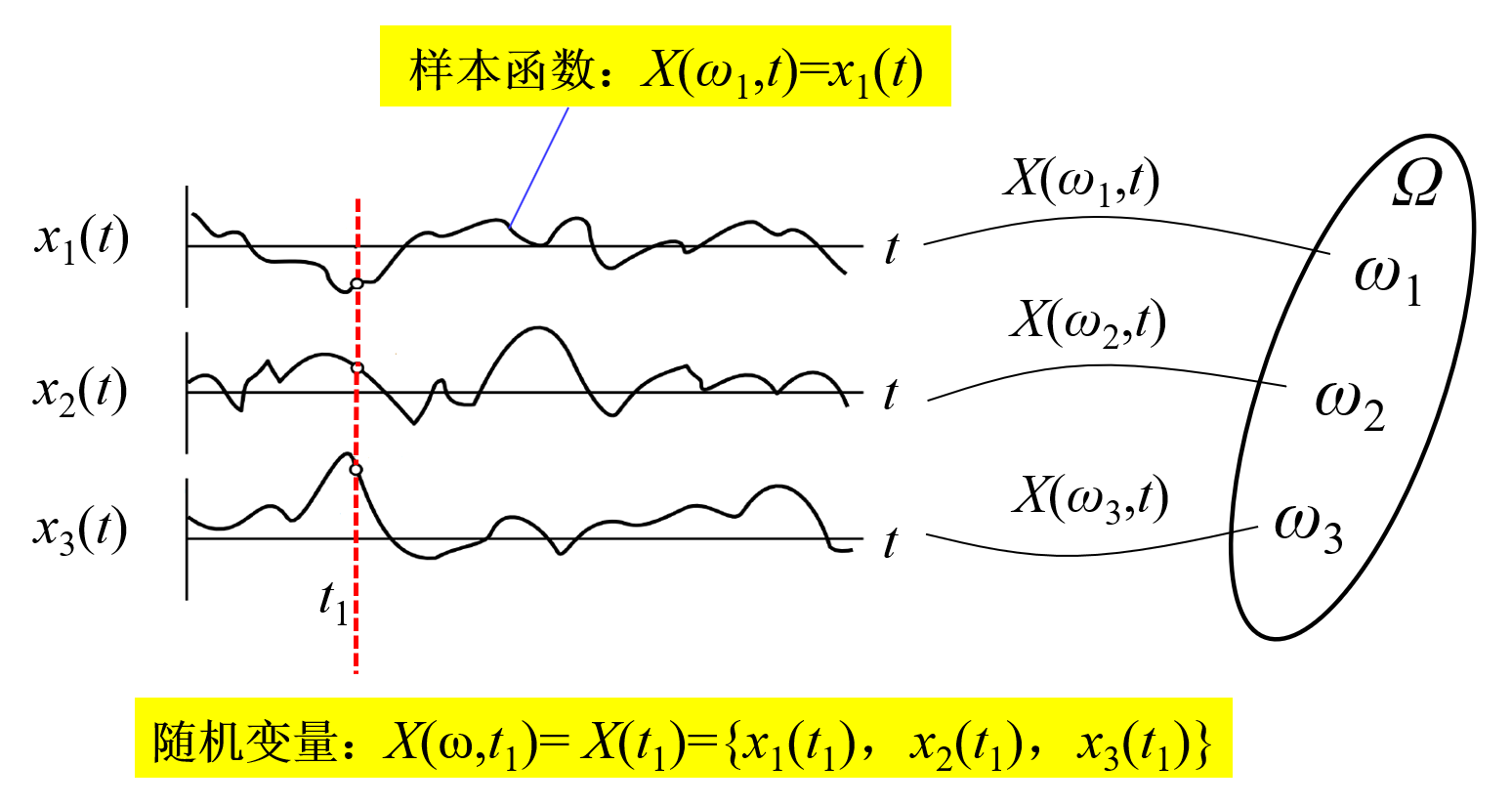
图5 随机过程试验结果与随机过程定义

随机过程定义：随机过程X(ω,t)是定义在Ω×T上的二元函数。对于固定的ω，X(ω,t)是时间t的函数，称为样本函数或样本轨道，简记为x(t)；对于固定的t，X(ω,t)是样本点ω的函数，称为随机变量，简记为X(t)。

一个样本函数x(t)对应着随机试验中的一次“测量结果”，即人们实际观察到的随机现象随时间演变过程，因此样本函数x(t)也被称为随机过程的一个“实现”。

随机变量X(t)描述的是所有样本函数x₁(t)，x₂(t)，…，x_n(t)在t时刻的取值，即所有质点在t时刻的空间位置分布情况。

显然，随机变量 X(t)和样本函数 x(t)具有完全不同的物理意义。随机变量X(t)用来描述大量质点在t时刻的浓度分布情况（统计规律），样本函数x(t)则用来描述一个质点的位移随时间的变化过程。

根据图5所示的随机过程定义，图1(a)所示的一个布朗粒子在t时刻的位移x(t)只能被抽象为固定样本点ω时的随机过程X(ω,t)，亦即样本函数x(t)。

但是，《随机过程》教科书却将布朗运动一个布朗粒子在t时刻的位移x(t)抽象为随机变量，把随机变量和样本函数这两个完全不同的数学概念当作同一个概念使用，出现了 “混淆概念”或“偷换概念”的逻辑错误，从根本上破坏了《随机过程》布朗运动理论的逻辑完备性和客观真理性。 

3、与《物理学》和《随机信号分析》矛盾

表1给出了《物理学》、《随机过程》和《随机信号分析》这三门学科对布朗运动现象及规律的数学描述，图中红字部分表示该结论与实验结果不符。

表1 不同学科对布朗运动现象及规律的数学描述

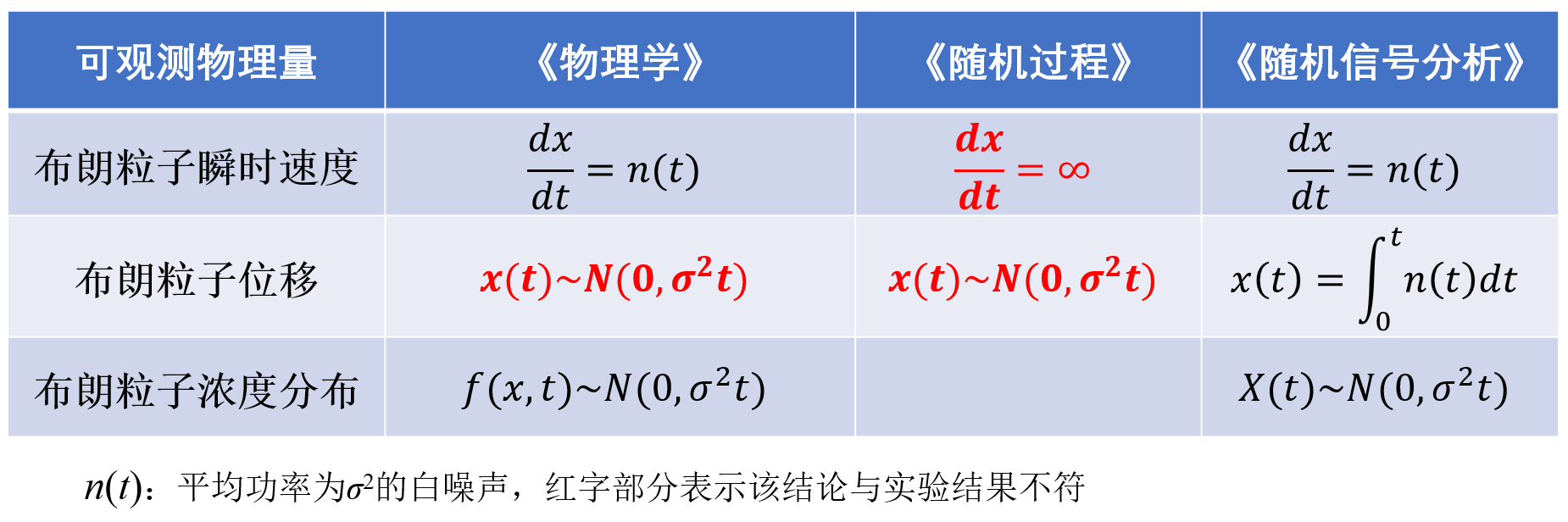
在国际标准《IEEE Standard Specification Format Guide and Test Procedure for Single-Axis Laser Gyros（IEEE 647-2006）》和中华人民共和国国家军用标准《光纤陀螺仪测试方法（GJB2426A-2004）》中，随机游走（布朗噪声）就是按照表1中《随机信号分析》布朗运动位移公式定义的，《随机信号分析》布朗运动理论已经在惯性导航技术等工程技术领域获得成功应用。

 《随机过程》布朗运动理论与《物理学》和《随机信号分析》中的布朗运动理论和实验结果矛盾和冲突，表明《随机过程》是一门理论与实践严重脱节的应用数学学科。

四、反常问题与范式转换

一旦某个科学理论中出现理论与经验事实不符、与其它科学理论矛盾或冲突、逻辑上不能自洽和违反科学基本常识等一系列反常问题，则预示该理论将面临库恩（Kuhn）在《科学革命的结构》书中所描写的科学危机和范式转换（图6），原有理论和方法将会被新理论和新方法所取代，导致科学知识体系和人类思维方式发生根本性的变革，从而把人类对客观世界的认识提高到一个崭新的水平，引发一场深入持久的科学革命。

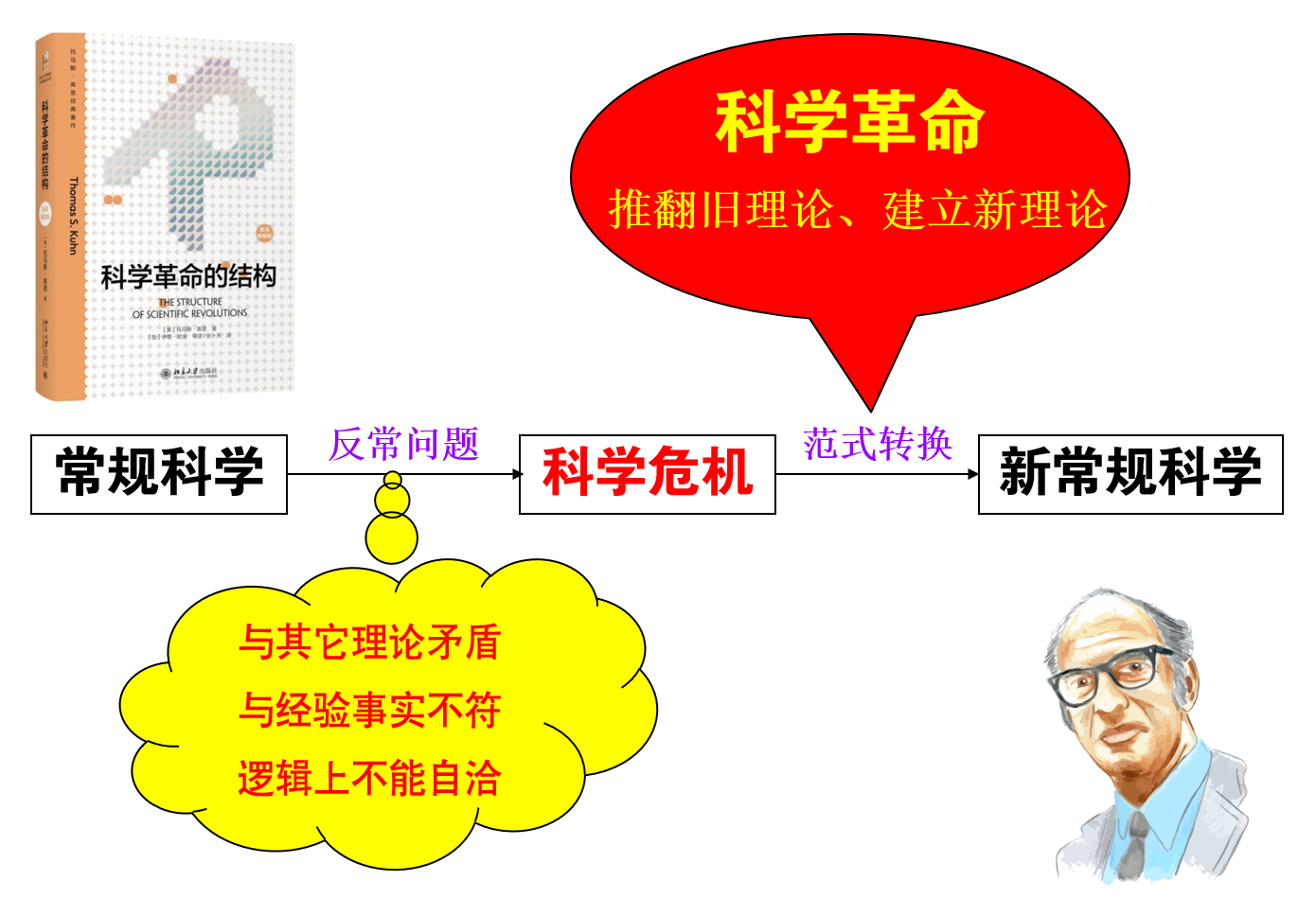
图6 库恩范式转换模型

参考：

布朗运动理论中的反常问题及原因分析（预印本）

《随机过程》布朗运动理论的常识检验、实验检验和逻辑检验