博文
基于双尺度约束模型的BN结构自适应学习算法
|
引用本文
戴晶帼, 任佳, 董超, 杜文才. 基于双尺度约束模型的BN结构自适应学习算法. 自动化学报, 2021, 47(8): 1988-2001 doi: 10.16383/j.aas.c180226
Dai Jing-Guo, Ren Jia, Dong Chao, Du Wen-Cai. BN structure adaptive learning algorithm based on dual-scale constraint model. Acta Automatica Sinica, 2021, 47(8): 1988-2001 doi: 10.16383/j.aas.c180226
http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c180226
关键词
贝叶斯网络,结构学习,约束模型,遗传算法
摘要
在无先验信息的情况下, 贝叶斯网络(Bayesian network, BN)结构搜索空间的规模随节点数目增加呈指数级增长, 造成BN结构学习难度急剧增加. 针对该问题, 提出基于双尺度约束模型的BN结构自适应学习算法. 该算法利用最大互信息和条件独立性测试构建大尺度约束模型, 完成BN结构搜索空间的初始化. 在此基础上设计改进遗传算法, 在结构迭代优化过程中引入小尺度约束模型, 实现结构搜索空间小尺度动态缩放. 同时, 在改进遗传算法中构建变异概率自适应调节函数, 以降低结构学习过程陷入局部最优解的概率. 仿真结果表明, 提出的基于双尺度约束模型的BN结构自适应学习算法能够在无先验信息的情况下保证BN结构学习的精度和迭代寻优的收敛速度.
文章导读
贝叶斯网络(Bayesian network, BN)理论为不确定性知识的表示, 节点间复杂关系的表达和信息融合推理提供了有效的模型框架[1-3]. 然而, 与其他图形化模型学习方法类似, BN也存在研究对象节点增加导致候选结构数量呈指数级增长的问题. 因此, 从大规模候选结构集合中快速, 准确地获得一个与数据样本匹配程度最优的结构模型是BN结构学习亟待解决的问题之一.
研究人员尝试利用条件独立性(Conditional independence, CI)测试度量节点间的依赖关系, 然后构造满足这些依赖关系的模型结构[4-6]. 但该类型学习方法运算次数一般为节点个数的指数次幂, 当面对节点数量较多的复杂网络时, CI测试效率较低. 与此同时, 研究人员将模型先验信息作为约束条件, 并与结构评分函数和搜索算法组合, 共同完成BN结构学习[7-10]. 但该类型方法在模型先验信息不准确或发生错误的情况下, 将导致结构学习结果精度低或陷入局部最优. 为此, 文献[11]通过构建不确定先验信息的评分函数并设计先验搜索算子, 提高对错误先验信息的适应能力. 但该方法并不能完全消除错误先验信息对BN结构学习产生的负面影响. 此外, 研究人员将节点间依赖关系检验与结构优化学习方法相结合, 进行无先验信息情况下的BN结构学习[12-13]. 在该思路下, 文献[14]提出了一种混合式BN结构学习方法, 该方法通过计算互信息量(Mutual information, MI)构造基于支撑树权重矩阵的节点序适应度函数, 利用改进遗传算法(Genetic algorithm, GA)获得节点排序, 最后将节点排序作为K2算法的输入进行结构学习; Wong等和Ji等分别将低阶CI测试引入进化算法和蚁群优化算法, 利用CI测试辨识部分节点对的独立关系以缩小结构搜索空间, 在此基础上利用评分函数和启发式搜索以获得BN结构[15-16]; Li等则提出I-GREEDY-E算法[17], 该算法首先在空图上计算节点间的MI以确定无向边, 然后利用CI测试确定边的指向, 最后在等价类模型空间中利用贪婪搜索算法获得BN结构. 上述学习方法在无先验信息的情况下实现了对结构搜索空间的约束, 并在约束空间内利用搜索方法获得了模型结构, 一定程度上提高了多节点复杂网络结构的学习效率. 然而, 在无先验信息的情况下, 以CI测试或MI检验为约束条件构造的结构搜索空间尺度固定, 无法在结构学习过程中动态调整结构搜索空间的规模大小, 易导致潜在最优解丢失.
针对上述问题, 提出基于双尺度约束模型的BN结构自适应学习算法(BN structure adaptive learning algorithm based on dual-scale constraint model, DSC-AL). 该算法将最大互信息(Maximum mutual information, MMI)和CI测试结合建立结构搜索空间的大尺度约束模型, 限制BN结构搜索空间的规模, 完成结构搜索空间的初始化. 借鉴GA迭代寻优过程完成BN结构学习. 在迭代寻优过程中建立小尺度约束模型完成搜索空间动态调整, 构建变异概率的自适应调节函数, 提高GA全局搜索能力. 在实验仿真中, 选择了不同节点规模的标准BN模型和不同样本量对DSC-AL算法的有效性进行测试, 并通过与Lee等提出的基于双重GA编码的BN结构学习算法[18]和Gheisari等构建的基于粒子群优化的BN结构学习方法[19], 以及经典的K2算法[20]进行性能对比, 验证DSC-AL算法的性能.
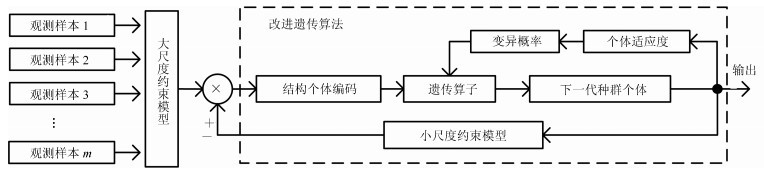
图 1 DSC-AL算法框架示意图
图 2 小尺度约束模型工作原理
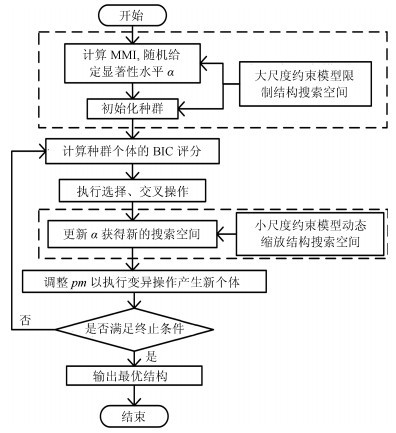
图 3 DSC-AL算法流程图
从大规模候选结构集合中快速, 准确地获得一个与数据样本匹配程度最优的结构模型是BN结构学习亟待解决的问题之一. 为此, 提出了一种基于双尺度约束模型的BN结构自适应学习(DSC-AL)算法, 解决了在无先验知识的情况下, 通过数据样本信息动态限制搜索空间, 高效挖掘节点间相关性的BN结构学习问题. 该算法在MMI和CI测试的双重约束条件下产生GA的初始种群, 获得BIC评分高的种群个体, 加快收敛速度; 通过在个体编码中引入CI测试的显著性水平, DSC-AL算法在进化过程中利用更新模型不断调整显著性水平的大小, 使得对应的搜索空间动态, 合理地变化, 提高算法的全局搜索能力; 同时充分利用种群个体的适应度分布自适应地调节变异概率, 克服算法的早熟收敛. 仿真结果验证了本文算法对解决BN结构学习问题的有效性, 该算法能够确保种群个体的多样性, 提高结构学习的精度和迭代寻优的收敛速度.
作者简介
戴晶帼
海南大学信息科学技术学院博士研究生. 主要研究方向为贝叶斯网络, 智能优化.E-mail: djgolivia_edu@126.com
董超
国家海洋局南海调查技术中心副研究员. 主要研究方向为智能控制.E-mail: dongchaoxj888@126.com
杜文才
中国澳门城市大学数据科学研究院教授, 海南大学信息科学技术学院教授. 主要研究方向为数据挖掘, 物联网技术. E-mail: wencai@hainu.edu.cn
任佳
海南大学信息科学技术学院教授. 主要研究方向为智能控制, 机器学习. 本文通信作者.E-mail: renjia@hainu.edu.cn
https://blog.sciencenet.cn/blog-3291369-1350961.html
上一篇:基于随机配置网络的井下供给风量建模
下一篇:含未知动态与扰动的非线性系统神经网络嵌入学习控制