博文
GWAS分析中SNP解释百分比PVE | 第四篇,MLM模型中如何手动计算PVE?
||
「系列部分:」
GWAS分析中SNP解释百分比PVE | 第一篇,SNP解释百分比之和为何大于1?
GWAS分析中SNP解释百分比PVE | 第二篇,GLM模型中如何计算PVE?
GWAS分析中SNP解释百分比PVE | 第三篇,MLM模型中如何计算PVE?
今天介绍一下如何手动计算MLM模型GWAS的PVE结果。因为GAPIT中的MLM模型又PVE结果,但是常用的GEMMA、GCTA的GWAS结果并没有PVE,本篇介绍一下如何根据GWAS结果手动计算,用R语言进行演示。
1. 参考文献
首先是这个论坛的内容:How to determine the percent phenotypic variation explained (PVE) by a selected SNP?
❝Feofanova, Elena. (2020). Re: How to determine the percent phenotypic variation explained (PVE) by a selected SNP?. Retrieved from: https://www.researchgate.net/post/How_to_determine_the_percent_phenotypic_variation_explained_PVE_by_a_selected_SNP/5e1600dd661123743209bc17/citation/download.
❞
里面介绍了计算方法:
 其中参考的文献是:
其中参考的文献是:
❝Shim, H., Chasman, D.I., Smith, J.D., Mora, S., Ridker, P.M., Nickerson, D.A., Krauss, R.M., and Stephens, M. (2015). A multivariate genome-wide association analysis of 10 LDL subfractions, and their response to statin treatment, in 1868 Caucasians. PLoS One 10, e0120758.
❞
整个公式如下:
 最后,完整的公式如下:
最后,完整的公式如下: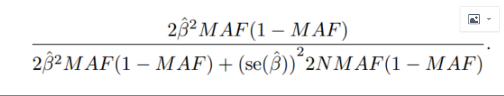 其中:
其中:
为GWAS中的effect值 MAF 为SNP的MAF次等位基因频率 为GWAS中effect值的标准误(se) N 为GWAS中该SNP参与分析的个体数
2. GAPIT中MLM模型分析PVE值
gaipit中的MLM模型代码如下:
# GWAS 分析
library(data.table)
source("http://zzlab.net/GAPIT/GAPIT.library.R")
source("http://zzlab.net/GAPIT/gapit_functions.txt")
myGd = fread("mdp_numeric.txt",header=T,data.table = F)
myGM = fread("mdp_SNP_information.txt",header = T,data.table=F)
myY = fread("dat_plink.txt",data.table = F)
head(myY)
covar = fread("cov_plink.txt",data.table = F)[,-1]
names(covar)[1] = "Taxa"
head(covar)
myGAPIT = GAPIT(Y = myY[,c(1,3)],GD = myGd, GM = myGM,
# PCA.total=3,
CV = covar,Random.model=TRUE,
model="MLM")对结果进行处理,计算PVE值,结果如下:
a2 = fread("05_lmm_gapit/GAPIT.MLM.V3.GWAS.Results.csv") %>% arrange(P.value) # GAPIT MLM
a2$PVE = a2$Rsquare.of.Model.with.SNP - a2$Rsquare.of.Model.without.SNP
head(a2)
a2 = a2 %>% select(1,lmm_effect = effect,maf = maf,lmm_p.value = P.value,
lmm_FDR_p = `FDR_Adjusted_P-values`,
lmm_Rsquare_with_snp = Rsquare.of.Model.with.SNP,
lmm_Rsquare_without_snp = Rsquare.of.Model.without.SNP,
lmm_Rs = Rs)
head(a2) 这里,GWAS结果中,因为没有effect的se的值,所以无法手动运算,下面我们看一下GEMMA和GCTA的fast-GWA,用同样的数据,进行GWAS分析,并手动计算PVE值,和GAPIT中的MLM模型的PVE值进行对比。
这里,GWAS结果中,因为没有effect的se的值,所以无法手动运算,下面我们看一下GEMMA和GCTA的fast-GWA,用同样的数据,进行GWAS分析,并手动计算PVE值,和GAPIT中的MLM模型的PVE值进行对比。
3. GEMMA进行MLM模型的GWAS分析
GEMMA进行GWAS分析,分为两步:
第一步:构建G矩阵 第二部:进行MLM的GWAS分析
# 构建G矩阵 gemma-0.98.1-linux-static -bfile ../geno/b -gk 2 -p p1.txt # 进行LMM分析 gemma-0.98.1-linux-static -bfile ../geno/b -k output/result.sXX.txt -lmm 1 -p p1.txt -c cov.txt
结果如下: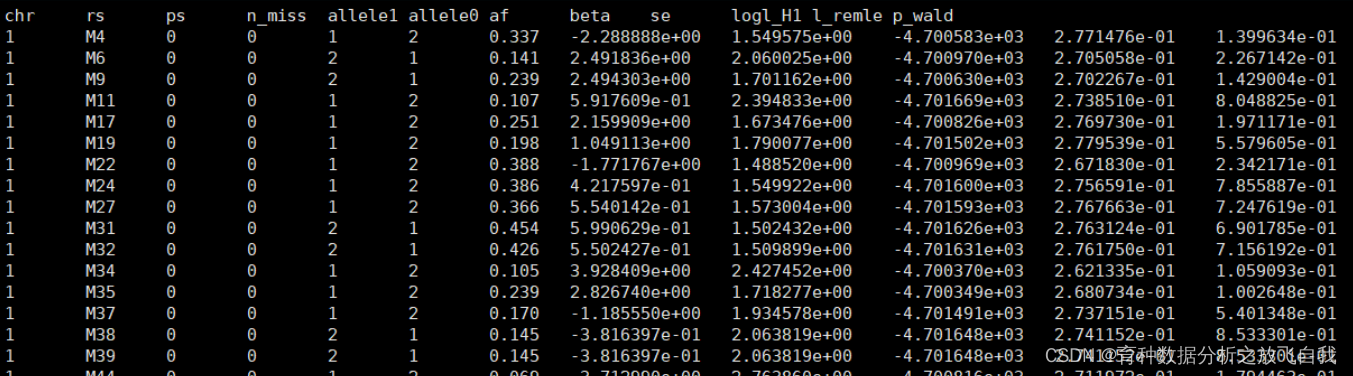 结果中:
结果中:
beta为effect se为se p_wald 为P值 n_miss 为总个体数的缺失,n为总个体数减去缺失 af为maf次等位基因频率
所以上面结果,读到R语言中,用下面公式进行计算PVE: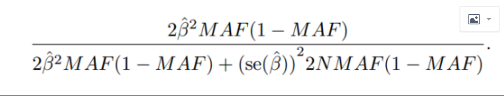 这里的N为1000,计算结果如下:
这里的N为1000,计算结果如下:
a4$pve = (2*(a4$beta^2*a4$af*(1-a4$af)))/(2*a4$beta*a4$af*(1-a4$af) + a4$se^2*2*1000*a4$af*(1-a4$af)) head(a4)

比较GAPIT的MLM模型的PVE和手动根据GEMMA的MLM计算的PVE结果,可以看到SNPM98663,它的PVE在GAPIT中是0.01815,在GEMMA中是0.01988,结果有些差异,下面我们看一下相关系数。
「比较相关系数:」
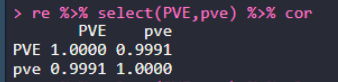
re = merge(a2,a4,by.x="SNP",by.y = "rs") head(re) re %>% select(P.value,p_wald) %>% cor re %>% select(effect,beta) %>% cor re %>% select(PVE,pve) %>% cor re %>% select(PVE,pve) %>% plot
GAPIT和GEMMA的P值比较结果:0.9986,基本一致。

GAPIT和GEMMA的effect值比较结果:0.9996,基本一致。
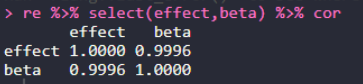 GAPIT和GEMMA的PVE值比较结果:0.9991,基本一致。
GAPIT和GEMMA的PVE值比较结果:0.9991,基本一致。
 两款软件的PVE的散点图:
两款软件的PVE的散点图: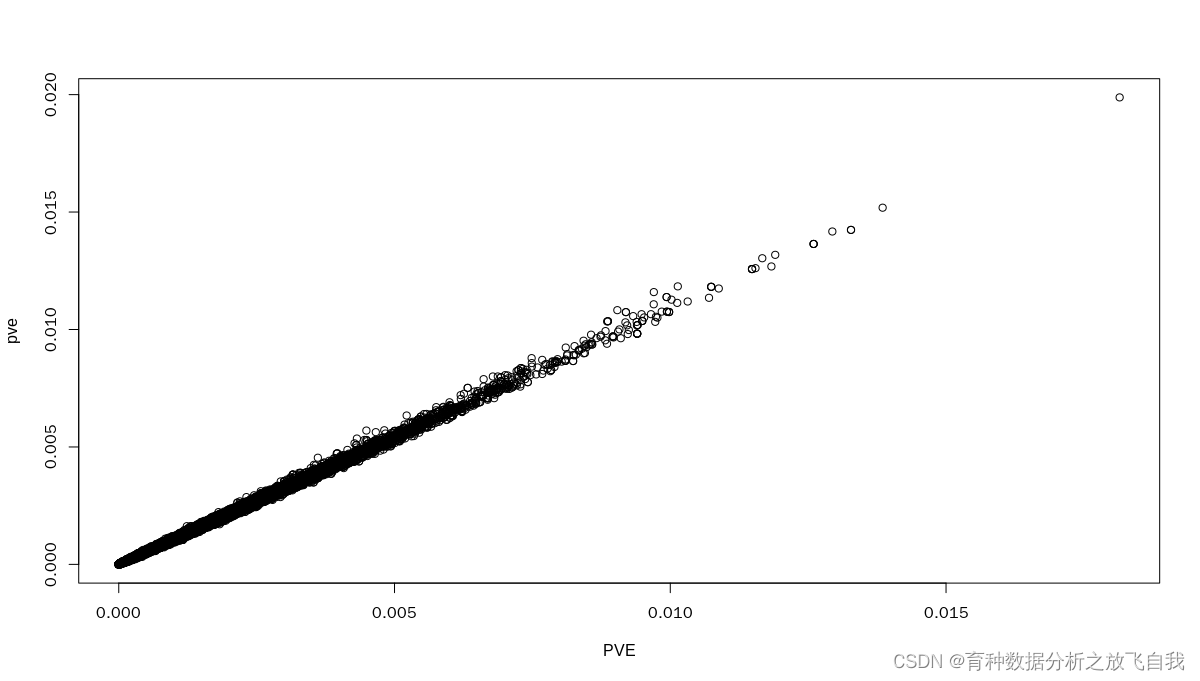 可以看到,上面的手动计算方法,和GAPIT的MLM模型的PVE结果完全一致。
可以看到,上面的手动计算方法,和GAPIT的MLM模型的PVE结果完全一致。
4. GCTA进行MLM模型的GWAS分析
GCTA进行GWAS分析,分为两步:
第一步:构建G矩阵 第二步:生产稀疏矩阵 第三步:进行MLM的GWAS分析
gcta --bfile ../geno/b --make-grm --out geno_grm --make-grm-alg 1 gcta --grm geno_grm --make-bK-sparse 0.05 --out sp_grm gcta --bfile ../geno/b --grm-sparse sp_grm --fastGWA-mlm --pheno dat_plink.txt --qcovar cov_plink.txt --out a1
生成的结果如下:
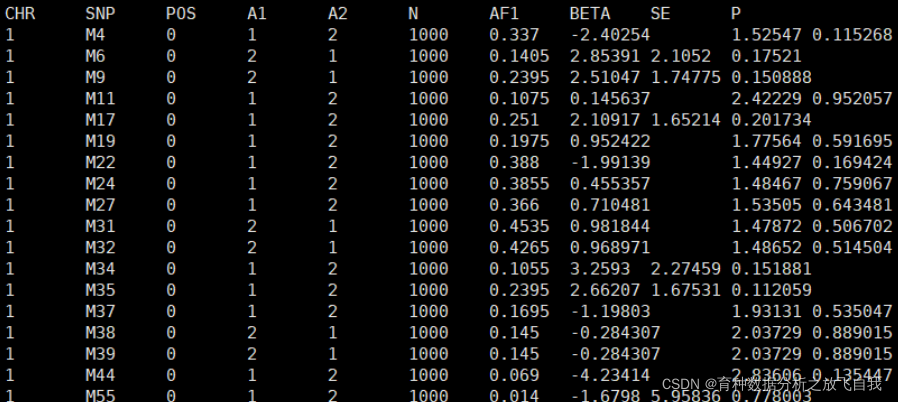
下面,我们读入到R语言中,手动计算PVE值。
a5 = fread("10_fast_GWA_MLM/a1.fastGWA") %>% arrange(P)
head(a5)
a5$pve = (2*(a5$BETA^2*a5$AF1*(1-a5$AF1)))/
(2*a5$BETA*a5$AF1*(1-a5$AF1) + a5$SE^2*2*1000*a5$AF1*(1-a5$AF1))
head(a5)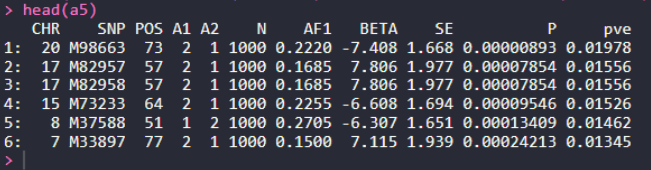
和GAPIT的MLM模型比较PVE结果:
re = merge(a2,a5,by.x="SNP",by.y = "SNP") head(re) re %>% select(P.value,P) %>% cor re %>% select(effect,BETA) %>% cor re %>% select(PVE,pve) %>% cor re %>% select(PVE,pve) %>% plot
结果如下:
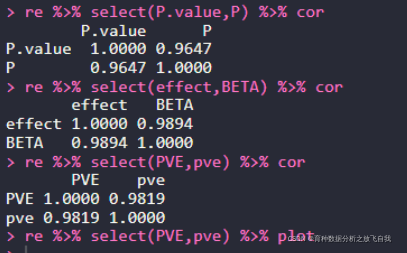 P值相关系数为0.96,effect相关系数为0.98,PVE相关系数为0.98,基本一致。
P值相关系数为0.96,effect相关系数为0.98,PVE相关系数为0.98,基本一致。
5. GEMMA和GCTA手动计算PVE结果可行
所以,经过上面的测试,我们可以得到结论:
对于GEMMA和GCTA软件,计算的GWAS结果,可以根据公式计算PVE 结果和GAPIT结果一致
所以,网站上面各种搜索GEMMA如何计算PVE,GCTA如何计算PVE,EMMA如何计算PVE的各种问题,可以休矣。
6. 讨论
读到此,你是否有一种豁然开朗的感觉,GWAS分析中显著SNP如何计算解释百分比(PVE)的相关问题,终于解决了。
当然,有些GWAS方法是没有给出se的,比如FAMcpu等,那就不能用这种方法进行手动计算了。
需要注意的是,PVE的方法,之和远远大于1,是因为显著SNP之间存在LD,因为SNP代表的是基因,如果存在LD较高,那就是基因被代表了很多次,所以PVE就会偏高,我们不能说8个SNP解释了表型60%的变异,因为这8个SNP可能是连锁的,他们之和被高估了。
另外,从理论上来说,PVE的上限是遗传力(h2),比如GEMMA的结果中:给出的PVE是所有SNP的PVE之和,从算法上来说,就是Va/(Va+Ve),就是遗传力。所以这里,给出所有PVE之和的上限就是遗传力。
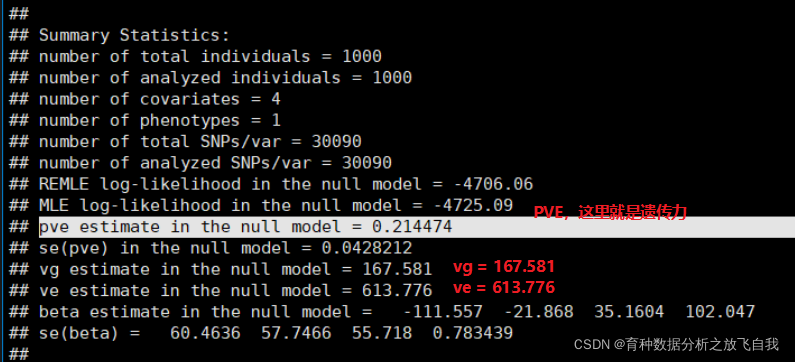
所以,在描述结果是,如果你的性状遗传力为0.3,那就表示你所有的SNP的解释百分比之和理论上限是30%,如果你计算的10个显著性的SNP的PVE之和为40%,然后还说自己的SNP多么牛叉,多么重要,这明显是不合适的,里面有很大重复估计的PVE在里面。
当然,相对于GLM的PVE计算(也就是R语言的单标记回归计算R-squared),MLM的计算方法重复估计偏低一点。之前的博客中有比较,同样的数据,GLM的PVE之和为50,而MLM的PVE之和为25。
最后,如果想要更严谨的计算多个SNP的解释百分比,或者一个区段内显著SNP的解释百分比(PVE),可以将该区段作为随机因子,在LMM模型中估算其方差组分,然后计算Vsnp/Vtotal的比值,这应该会降低假阳性,是更严谨的方法。具体文献见:
❝Citation: Tang Z, Xu J, Yin L, Yin D, Zhu M, Yu M, Li X, Zhao S and Liu X (2019) Genome-Wide Association Study Reveals Candidate Genes for Growth Relevant Traits in Pigs. Front. Genet. 10:302. doi: 10.3389/fgene.2019.00302
❞
里面将显著的SNP区段作为block,进行方差组分的估计,进而计算PVE: 之前,在星球内,有朋友问我如何计算PVE,我当时给了三个方法:
之前,在星球内,有朋友问我如何计算PVE,我当时给了三个方法:
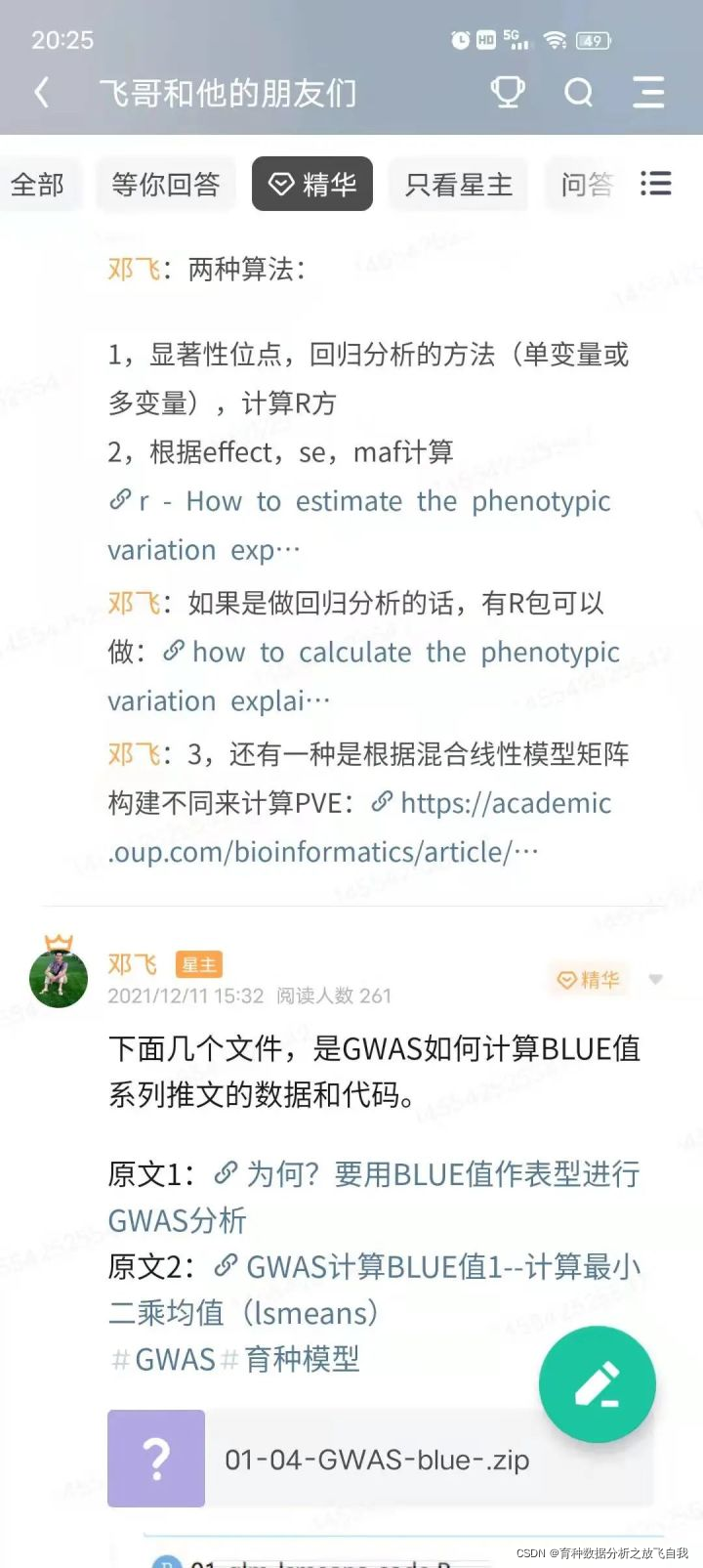
第一种:是使用R语言的回归分析去做,这个也是GLM的GWAS计算PVE的方法 第二种:是根据effect、se,maf去计算,这个也是MLM的GWAS计算PVE的方法 第三种:是将显著的区段(block)放到LMM模型中,计算PVE,这个就是上面文献计算的方法。
「2021年圣诞节的周六,花了一上午进行了PVE不同方法的整理,相信会对有相关疑惑的人有所帮助,我浏览了各种论坛,都没有找到一个确切的方案。这里,我用实际数据进行了测试,总结了几种方法,所以,你看到的应该是互联网上第一篇使用的方案,赶紧点个赞吧!」
❝欢迎关注我的公众号:
❞育种数据分析之放飞自我。主要分享R语言,Python,育种数据分析,生物统计,数量遗传学,混合线性模型,GWAS和GS相关的知识。
下一篇,将相关的资料,整理为一个pdf,将相关论文,资料,代码,数据进行一个整理,方便需要的朋友进行重演和测试,欢迎继续关注。
https://blog.sciencenet.cn/blog-2577109-1318085.html
上一篇:GWAS分析中SNP解释百分比PVE | 第三篇,MLM模型中如何计算PVE?
下一篇:R语言相关性分析和相关性分析可视化常用方法汇总