博文
《周易》筮法溯源初探
|
《周易》筮法溯源初探
[摘 要]对《周易·系辞》的《大衍》章中的“大衍之数五十”“其用四十有九”“挂一以象三”这三个争议较大的
焦点的阐释作了一个较为全面的回顾与总结,在对目前存世的几种《周易》筮法的概率分析的基础上,根据张
政烺先生的《试释周初青铜器铭文中的易卦》一文中对“其中四十有九”的阐释,在《筮仪》的基本构架下,构建
了《周易》筮法的一种新的推演方法.新筮法与《左传》《国语》筮例的拟合度达到了68.24%.
[关键词]《周易》筮法;概率分析;筮法改造;《左传》《国语》筮例;分布拟合检验
1.《周易》筮法及概率分析概述
《周易·系辞》的《大衍》章是专门阐释《周易》筮法的一章.目前存世的《大衍》章有两个版本,其一是唐孔 颖达奉太宗之命,基于魏王弼《周易注》而编修的《周易正义》,其中,《大衍》章属《系辞》(上)的第八章,从“大 衍之数五十,其用四十有九.”开始,到“显道是故可与酬酢,可与祐神矣”,不算标点符号,共186个字[1].
南宋诸儒多认为此本存在错简,其中朱熹在《周易本义》中对《系辞》作了较大调整,将《大衍》章调整 为《系辞》(上)的第九章,将“天一,地二;天三,地四;天五,地六;天七,地八;天九,地十”作为《大衍》章的 开篇,后继则为“天数五,地数五,五位相得而各有合.天数二十有五,地数三十,凡天地之数五十有五,此 所以成变化而行鬼神也”,接下来则是“大衍之数五十,其用四十有九.分而为二以象两,挂一以象三,揲之 以四,以象四时,归奇于扐以象闰,五岁再闰,故再扐而后挂.乾之策二百一十有六,坤之策百四十有四,凡 三百有六十,当期之日.二篇之策,万有一千五百二十,当万物之数也.是故四营而成易,十有八变而成卦, 八卦而小成.引而伸之.触类而长之,天下之能事毕矣.显道是故可与酬酢,可与祐神矣”,并将“子曰:‘知变化之道者,其知神之所为乎?’”提上来作这一章的结尾.[2]
这两种版本后世各有取舍:清李光地奉旨编纂的《周易折中》[3]、对现代易学影响较大的吉林大学教 授金景芳之《周易讲座》[4]均承袭《周易本义》,近年逐渐引起关注的尚秉和之《周易尚氏学》[5]与黄寿祺、张 善文之《周易译注》[6]则承袭孔本.
两者对《周易》筮法的阐释大致相同,揲蓍成卦之法均是四营成易、三变成爻、十有八变而成一卦,《周 易本义》卷首的《筮仪》篇有详细说明,明清以来,易界学人多采信之.异于《筮仪》又影响揲蓍结果的阐释 主要集中在对“挂一以象三”有不同的解释:在《筮仪》中,三揲皆需挂一;而宋张载《横渠易说》的阐释是初 揲挂一,二、三揲皆不挂一[7];今人向传三先生于上个世纪90年代提出三揲皆左右各挂一策,其文载于《周 易研究》1997年第4期[8].
对《周易》筮法的参研,一般有两项基本材料:一为《周易·系辞》,二为《左传》《国语》所载筮例. 《左传》 《国语》关于《周易》筮例的记载共有16条,占卦17个.具体是:“观之否、屯之比、大有之乾、归妹之睽、蛊、 大有之睽、复、艮之八(史谓艮之随)、困之大过、明夷之谦、屯、屯之比、坤之比、泰之需、乾之否、贞屯悔豫、 泰之八”[9].其中,对“泰之八”存在较大争议[10-13],暂舍之不用,这样共得16卦96爻. 《筮仪》筮得六七八九的概率分别是1/16,5/16,7/16,3/16[14-16],该分布列与《左传》《国语》筮例的拟合 度为 34.21%[16];后两种筮法与《左传》《国语》筮例的拟合度可参照文献[16]计算,计算结果均远小于 0.001,不足信.故而《筮仪》对周易筮法的阐释经过近十个世纪的漫长历史时期,成为学界对周易筮法的基 本共识,不是偶然的.
另有一种源自于《火珠林》的“三钱筮法”流行甚广.清末明初杭辛斋在《学易笔谈》与《读易杂识》中各 有《火珠林》一篇,杭氏认为揲蓍而筮,常常“效反不著”,不若“易之以钱”.不过杭氏是这样解释的,“卜筮 实精神之学,非可专以形式求之”“遵用蓍策”则“需时甚久,欲意志不纷,终此六爻,殊非易易”,而“易之以 钱,缩短时间三分之二,庶心志不纷,精神易贯,阴阳变化,仍有合于大衍之数,而得‘乾元统天之意’,是以 后世习用不废”,并非“筮果有逊于钱”[17] .“ 用钱不用蓍”,严格地讲已不能称之为筮法了,本文姑且不论.该 筮法得老阴少阳少阴老阳的概率分别是1/8,3/8,3/8,1/8,与《左传》《国语》筮例的拟合度参照文献[16]计 算结果为35.37%.从《筮仪》筮法、“三钱筮法”与《左传》《国语》筮例的拟合度分别为34.21%与35.37%来 看,杭氏推崇“三钱筮法”几乎与《筮仪》筮法同等的地位是合适的.
比较由《筮仪》筮法与“三钱筮法”的概率分布率所形成的两个四维向量(1/16,5/16,7/16,3/16)与(1/8, 3/8,3/8,1/8),它们的终点都是四维空间中的超平面x+y+z+w=1上的点,利用向量的内积与向量的模的概 念,容易计算得两个向量的广义夹角约为12.6o,说明这两个向量分别指向不同的“方向”;两种筮法的概 率分布率关于《左传》《国语》筮例的拟合度基本相当,后者略高.于是推测:《筮仪》筮法与“三钱筮法”分别 对应了东周时代的周易筮法的不同侧面. 下面将试图在分二、挂一、揲四、归奇等四营的基本构架下,将《筮仪》筮法与“三钱筮法”合而为一,从 而得到一种与《左传》《国语》筮例具有较高拟合度的揲蓍而占的筮法,以期在《周易》筮法的溯源研究中愚者偶得.
2 对《周易》筮法的溯源研究及概率分析
2.1 “大衍之数五十”与“其用四十有九”
在《周易·系辞》的《大衍》一章中,对“大衍之数五十”与“其用四十有九”的阐释,自从汉代一直到唐 宋,众说纷纭,莫衷一是.对“大衍之数五十”有的拖出了北辰、天地、日月、春秋、三才、四时、五行、八方、十 干、十二支、二十四气、二十八宿这些数字来拼凑(马融、京房、司马迁、刘散,各家不同),有的用八(卦)乘 六(爻)再加上二(乾坤二用)来拼凑(荀爽),有的用“天地之数五十有五”减五来拼凑(郑玄、虞翻、姚信、董 遇、李鼎柞),有的用三、五、七、九、二、六、八、十(不用一、四)来拼凑(崔憬),等等,总之凑出个“五十”[18-19]. 王弼在《周易注》讲“演天地之数,所赖者五十也,其用四十有九,则其一不用也”,讲了等于没讲.朱熹 在《周易本义》中将“天一,地二;天三,地四;天五,地六;天七,地八;天九,地十.天数五,地数五,五位相得而各有合.天数二十有五,地数三十,凡天地之数五十有五,此所以成变化而行鬼神也”调整在“大衍之数 五十”之前,“大衍之数五十有五”几乎呼之欲出,然而朱子笔锋一转,终于还是借助于河图洛书,回到了 “大衍之数五十”上去了,至于对“其用四十有九”的注解则是:“盖出于理势之自然,而非人之知力所能损 益也”,也是讲了等于没讲.
大衍之数是五十还是五十有五,两汉时已莫衷一是,大衍之数“五十有五”,在汉魏时期就有相关说 法,到了宋代,陆秉、胡瑗等学者则明确撰文论述,遂为更多学者所接受和认同.在现代学术框架下论证大 衍之数“五十有五”,首推金景芳先生.之后,高亨、郭鸿林、廖名春、陈恩林、郭守信等先生,亦撰文论证这 一说法,使此说更具说服力[20]. 至于为何“其用四十有九”,宋代陆秉等人对“大衍之数五十有五,其用四十有九”的解释则过于拘泥 于占筮的形式而不是内容:“而用四十有九者,除六虚之位也.古者卜筮,先布六虚之位,然后揲蓍而六交 焉”,这样55减去6等于49,所以“其用四十有九”[21]. 金景芳先生则认为:“五十五策不全用,只用四十九策,古人曾做过种种解释,都是牵强附会,不足信 据.其实根本没有什么深意,只是因为五十五策全用最后得不出七八九六,不能达到筮的目的”[4],杨柳桥 先生则引郑玄之注,说得更加绝对:“只有用四十九这个数,才能够推出‘七、八、九、六’四个阴阳正变之数 来;不但五十不可能,其他的数都是不可能的”[18],金杨二位的结论值得商榷.事实上,笔者经过计算机系 统模拟推演,发现从五十五策或五十四策或五十三策或五十二策或五十一策或五十策开始推演,三变之 后,确实得不到六七八九;但从四十九策或四十八策或四十七策开始推演,三变之后也均可以得到六七八 九,从四十六策开始推演,三变之后可以得到六七八但得不到九;从四十五策开始推演,三变之后得到的 是五六七八而不是六七八九了.
2.2 《周易》筮法溯源初探
1978年底,在吉林大学召开的古文字学讨论会上,应参会人员的要求,会议组为著名古代史专家张 政烺先生安排了一次临时报告.张先生在会后进一步提炼,撰成《试释周初青铜器铭文中的易卦》等数文. 在《试》文中,张先生谈及周初的《周易》筮法时,根据马王堆帛书《周易·系辞》中没有《大衍》章,判断《大 衍》章是汉朝中期后的作品,并针对“大衍之数五十”却为何“其用四十有九”提出了自己的看法:“《周易· 系辞》说‘大衍之数五十,其用四十有九’,永远把一根蓍策搁起来,很无道理……笔者认为‘大衍之数五 十,其用四十有九’所反映出来的是占卦时并不是把全部蓍策都拿出来,以体现数的变易无定,后来僵化 了,成为固定的形式……‘大衍之数五十,其用四十有九’所反映出来的是占卦时并不是把全部蓍策都拿 出来,以体现数的变易无定……所用的数都固定起来,没有变化的可能了”.为此,张先生提出一种类似打 桥牌时上牌(也就是切牌)的办法,即每次虚置数根蓍策不用,置于到底虚置几策则事先不确定,这样随后 的四营三变可能是从阳数开始也可能是从阴数开始.当然上牌是把一副牌的前一部分移到后面,并不废 置.张先生这里借用“上牌”一词,指的是把筹策的一小部分取出搁置不用[22].
于是,受张先生的启示,笔者认为“大衍之数五十有五,其用四十有九”有两层涵义:第一,大衍之数五 十有五,但四营三变的揲蓍过程不能从五十五根蓍策开始,应该从中虚置数根蓍策不用,至于应该虚置多 少蓍策、揲蓍过程应该从多少蓍策开始,则应该事先不确定,以体现“易数无定”的易理;第二,四营三变的 揲蓍过程至多从四十九策开始,虚置蓍策数至少为六策,将“其用四十有九”理解成“其用至多四十有九”. 否则所用之数均是四十九,奇偶或阴阳固定下来,另一种可能的变化被莫名忽视了.
天地之间,阴阳消长,生生无已.少阳阶段,阴盛于阳但阳渐盛而阴渐消,少阳渐盛而至老阳;老阳阶 段,阳盛于阴且阳渐盛而阴渐消,老阳至极而生少阴;少阴阶段,阳盛于阴但阳渐消而阴渐盛,少阴渐盛而 至老阴;老阴阶段,阴盛于阳且阴渐盛而阳渐消,老阴至极而生少阳.周而复始,无尽无穷.筮者占筮时,手 握一把蓍策,通过分二、挂一、揲四、归奇四营三变,模拟天地阴阳消长变化,努力遵循的是天人感应法则, 孜孜以求的是天人合一的理想.于是笔者作大胆设想:首先,因为十为小盈之数,四十九与九关于模“十” 同余,所以四十九与九一样,同为老阳之数,四十八、四十七、四十六则分别视为少阴之数、少阳之数及老阴之数;其次,四营三变的揲蓍过程开始时的蓍策数可能是老阳之数四十九、少阴之数四十八、少阳之数 四十七、老阴之数四十六这四种中的某一种.从大衍之数五十五中,拿去老阴之数六则剩下老阳之数四十 九、拿去少阳之数七则剩下少阴之数四十八、拿去少阴之数八则剩下少阳之数四十七、拿去老阳之数九则 剩下老阴之数四十六,这种阴阳互补对偶现象可视为大衍之数五十有五的另一旁证.
如果四营三变从四十九策开始,那么筮得六七八九的概率分别是1/16,5/16,7/16,3/16,记之为四元 组即四维向量β1=(1/16,5/16,7/16,3/16). 如果四营三变从四十八策开始,那么可以参照文献[16],类似推算筮得六七八九的概率分别是1/8, 3/8,3/8,1/8,记之为向量β2=(1/8,3/8,3/8,1/8).值得注意的是,这一概率分布列与“三钱筮法”相同. 如果四营三变从四十七策开始,那么可以推算出筮得六七八九的概率分别是3/16,7/16,5/16,1/16, 记之为向量β3=(3/16,7/16,5/16,1/16). 如果四营三变从四十六策开始,那么可以推算出筮得六七八九的概率分别是1/4,1/2,1/4,0,记之为 向量β4=(1/4,1/2,1/4,0). 不难验证β1与β2相互之间不能表示,也就是线性无关,但是β3与β4则可以由β1与β2线性表示:β3=-β1+2β2、β4 =-2β1+3β2.这样,β3与β4的全部信息均包含在β1与β2之中,也就是说,从四十七策或四十六策开始 的四营三变所蕴含的信息均包含在从四十九策或四十八策开始的四营三变之中.这样在占筮时只要推演 从四十九策或四十八策开始的四营三变即可,而且这两种情况不能相互取代.
这里暂且撇开“大衍之数五十有五”与“大衍之数五十”的纷争,仍然在《筮仪》的基础上,从五十策开 始.为体现易数的变易无定,虚置一策或二策不用、从四十九策或四十八策开始四营三变,这样筮得六七 八九的概率就是β = t·β1 +(1-t)·β2,这里t是介于0~1之间的某一常数,以表示β1与β2的权重. 至于如何确定t值,则有两种考虑的角度.
首先从数理统计的角度推算.以《左传》《国语》筮例为标的,合理的设想是t的取值应该使得β与《左 传》《国语》筮例的拟合度达到最大值.将 β1与β2 的分量值代入,得
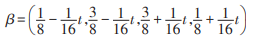 (1)
(1)
假设筮得六七八九的概率如式(1)所示,现独立重复进行试验96次,记六七八九出现的次数分别是 X1、X2、X3、(96-X1-X2-X3),则X1、X2、X3的联合概率分布列为
 (2)
(2)
在96次独立重复试验中,筮得六七八九的理论频数(记为向量形式)是
96·β =(12-6t,36-6t,36+6t,12+6t) (3)
在《左传》《国语》筮例样本的96爻中,六七八九的实际频数是(10,32,43,11),理论频数向量与实际 频数向量的欧氏距离记为d(t),则
 (4)
(4)
在公式(2)所示的多项分布的概率分布列中,求出与理论频数向量96·β的距离的平方大于等于[d(t)]2的 所有样本点对应的概率的和,这就是β与《左传》《国语》筮例作分布拟合检验的拟合度,记之为P(t),具体表 达式是
 (5)
(5)
其中IF()是逻辑判断函数,第一参数logical是指如下逻辑判别式
 (6)
(6)
如果logical的值为"TRUE",那么返回第二参数的值,如果logical的值为“FALSE”,那么返回第三参数的值,(5)式中第三参数值为0.
表1给出函数P(t)在0~1之间的列表式表示,其中自变量保留2位小数,函数值保留4位小数.

观察可知,t值在0~0.5之间变化时,P(t)随t值的增加而增加,t值在0.5~1之间变化时,P(t)随t值的 增加而减少.在t =0.5时P(t)取得最大值0.662 4.
其次,按照阴阳平衡的一般易理,49是奇数,48是偶数,以均衡的概率决定是从四十九策、还是从四 十八策开始四营三变,这样t也应该取值为1/2.
于是尝试在《周易本义·筮仪》每三变的第一变的四营之前增加一个预备步骤:从五十根蓍策随机取 出数根,检查奇偶.若为奇,则虚置一策不用、从四十九策开始四营三变,若为偶,则虚置二策不用、从四十 八策开始四营三变,其余推演过程不变.
3 结束语
公式(1)所示的概率分布列,t=1时,对应着《筮仪》从阳数四十九策开始的四营三变成一爻的揲蓍而筮 过程;t=0时,对应着从阴数四十八策开始的四营三变成一爻的揲蓍而筮过程,也同于“三钱筮法”的占筮过 程;t=1/2时,对应着新改造的筮法.根据《筮仪》筮法、“三钱筮法”与《左传》《国语》筮例的拟合度基本相当, 进而推测这两种筮法分别对应了《周易》筮法的不同侧面(阳的一面与阴的一面).在分二、挂一、揲四、归奇 四营的基本构架下,将两者合二为一、在《筮仪》基础上新改造成的筮法,与《左传》《国语》筮例的拟合度达 到66.24%,可信度极大提高.张政烺先生将“其用四十有九”解释为“其用至多四十有九”确为至论.
另一方面,本着阴阳平衡的一般易理,周易筮法筮得阴爻与阳爻的概率应该相等,而《左传》《国语》筮 例样本的96爻中,53爻是阴爻,43爻是阳爻,其中,阳爻占44.79%,这是一有偏的样本.如果假设《左传》 《国语》筮例样本是来自于一个筮得阴爻与阳爻的概率均是50%的筮法,重复筮96次而得到这样一个有 偏的样本、或者得到比该样本更加有偏的样本的概率之和,可以利用二项分布的概率分布律计算而得,计算结果是35.84%.所以新筮法与《左传》《国语》筮例的拟合度达到66.24%,已经是一个相当满意的结果了.
参 考 文 献
[1]孔颖达[唐].周易正义[M].北京:中国致公出版社,2009:268-271.
[2]朱熹.周易本义[M].北京:中华书局,2009:233-236.
[3]李光地.周易折中[M].成都:巴蜀书社,2008:426-431,535-538.
[4]金景芳,吕绍刚.周易讲座[M].长春:吉林大学出版社,1987:50-56.
[5]尚秉和.周易尚氏学[M].北京:中央编译出版社,2012:231-234.
[6]黄寿祺,张善文.周易译注[M].上海:上海古籍出版社,2001:548-553.
[7]张载.张载集[M].北京:中华书局,1983:194-197.
[8]向传三.周易筮法的概率研究[J].周易研究,1997(4):66-82.
[9]高亨.周易古经今注[M].北京:中华书局,1984:139- 160.
[10]刘轶“. 宜变之爻”与“之八”、“皆八”解赘论[J].社会科学,2016(4):164-170.
[11]王化平.“艮之八”、“泰之八”和“贞屯悔豫”新解[J].学行堂文史集刊,2012(1):7-11.
[12]廖名春《. 左传》《国语》易筮言“八”解[C]//2009年两岸四地《春秋》三传与经学文化学术研讨会,北京,2009:15-22.
[13]俞志慧《. 国语·晋语四》“贞屯悔豫皆八”为宜变之爻与不变之爻皆半说[J].中国哲学史,2007(4):68-76.
[14]董光璧.易学科学史纲[M].武汉:武汉出版社,1993:65-67.
[15]孙涤.解析大衍筮法及易卦的蓍占概率[J].文史哲,2018(1):47-59,166.
[16]王晓刚,宗序平.基于正态近似法《周易本义·筮仪》的概率分析[J].扬州职业大学学报,2019,23(1):30-34.
[17]杭辛斋.学易笔谈读易杂识[M].沈阳:辽宁教育出版社,1997:175-176,261-262.
[18]杨柳桥.先秦易学中的数理问题[J].辽宁大学学报(哲学社会科学版),1982(5):8-22.
[19]于成宝《. 周易》“大衍之数”略论[J].求索,2007(10):151-152,144.
[20]马金亮,丁鼎.大衍之数“五十有五”说补证[J].周易研究,2015(2):32-39.
[21]郭鸿林.评宋人陆秉对《周易》“大衍之数”的解说[J].周易研究,1992(1):5-8.
[22]张政烺.试释周初青铜器铭文中的易卦[J].考古学报,1980(4):403-415.
https://blog.sciencenet.cn/blog-113916-1292294.html
上一篇:基于正态近似法的《周易本义·筮仪》概率分析
下一篇:无题