连接无穷大的奇特数学与计算机科学的新桥梁

描述集合论家研究无穷大这一小众数学。如今，他们表明他们的问题可以用算法的具体语言来重写。

Joseph Howlett 撰文

左   芬       翻译

【译注：原文2025年11月21日刊载于QuantaMagazine，链接见文末。】

所有现代数学都建立在集合论的基础之上，而集合论研究的是如何将对象的抽象集体组织起来。不过一般来说，数学研究者在解决他们的问题时无需考虑它。他们可以理所当然地认为集合会展现他们所需要的行为，并继续开展工作。

描述集合论家则是个例外。这个小型的数学家社团从未停止过研究集合的基础本质——尤其是其他数学家忽视的奇特无穷集合。

他们的领域如今不再那么孤单了。2023年，一位名叫Anton Bernshteyn的数学家公布了描述集合论的遥远数学前沿与现代计算机科学之间的一种深刻而惊人的关联。

他证明，关于特定种类的无穷集合，所有问题都可以重写为关于计算机网络如何通信的问题。连接两个不同学科的这一桥梁让两边的研究者们都惊呆了。集合论家使用的语言是逻辑，而计算机科学家使用的语言则是算法。集合论处理无穷，而计算机科学处理有穷。完全没有理由他们的问题会相关，更别说等价了。

“这个结果相当诡异，”布拉格市查理大学计算机科学家Václav Rozhoň说道，“因为，你就没指望会得到这个。”

在Bernshteyn的成果出来之后，他的同行们一直在探索如何通过这座桥梁来回穿行以证明两侧的新定理，以及如何将这座桥梁推广到新的问题种类里去。一些描述集合论家甚至开始利用从计算机科学这一侧得到的见解来重构他们整个领域的景观，并重新思索他们理解无穷的方式。

Anton Bernshteyn致力于发掘和探索集合论与诸如计算机科学和动力系统这些更偏应用的领域之间的重要联系。

“一直以来我们都在做着非常类似的问题，可是彼此却从来没有直接讨论过，”卡内基梅隆大学描述集合论家Clinton Conley说道，“所有这类全新合作的大门就此打开了。”

集合的分裂

Bernshteyn在读研究生时首次听说描述集合论——被当做曾经辉煌过，但已经彻底没落的一个领域。过了一年多他才发现这位教授说的并不对。

2014年，作为伊利诺伊大学的一年级研究生，Bernshteyn选了Anush Tserunyan的一门逻辑学课程，而她后来成了他的导师之一。她纠正了这一偏见，“我还留在这个领域，功劳全在于她，”他说，“在她的呈现下，逻辑学和集合论确实就像是连接不同数学分支的胶水。”

描述集合论始于Georg Cantor，他在1874年证明有不同大小的无穷大。例如，整数（0,1,2，……）的集合跟所有分数的集合是同样大小的，但比所有实数的集合要小。

Anush Tserunyan将描述集合论视为把不同数学分支结合在一起的连接组织。

当时，数学家们对不同无穷的这种多样性感到极度不适。“你很难理解。”如今已在加州大学洛杉矶分校工作的Bernshteyn称。

部分出于对这种不适的回应，数学家们发展了另一种大小的概念——这种大小刻画了一个集合可能占据多少长度、面积或体积，而不再是它包含的元素的数目。这一大小的概念被称为集合的“测度”（与Cantor的大小概念，所谓集合的“基数”不同。）最简单的测度类型——Lebesgue测度——度量一个集合的长度。尽管从0到1的实数集与从0到10的实数集都是无穷的并且基数相同，前者具有Lebesgue测度1，而后者则具有Lebesgue测度10。

Georg Cantor发现数学上的无穷能以不同形状和大小出现。

为了研究更复杂的集合，数学家使用了不同种类的测度。一个集合越丑陋，能度量它的方式就越少。描述集合论想回答的问题就是，哪些集合可以用不同的“测度”定义来衡量。他们接着基于这些问题的答案把集合排成一种等级。在顶层的是容易构建并且能以你想要的任何测度概念进行研究的集合。在底层的则是“不可测”集合，它们极为复杂以致完全无法量度。“人们经常使用‘病态’这个词来形容，”Bernshteyn说道，“不可测集合相当糟糕。它们是反直觉的，并且行为很不好。”

这一等级不仅能帮助集合论家绘出他们领域的景观；它还为他们提供一些见解，告诉他们哪些工具可以用于解决其它数学领域中更典型的问题。在动力系统、群论以及概率论这些领域里的数学家需要知道他们所使用的集合的大小方面的信息。一个集合在等级中的位置决定了他们能使用哪些工具去解决他们的问题。

因此描述集合论家就好像是图书管理员，维护着由不同种类的无穷集合（以及度量它们的不同方式）组成的一个庞大的书架。他们的工作就是拿到一个问题，判定它的解需要多复杂的集合，然后把它恰当地放到书架上，以便其他的数学家记录下来。

做出抉择

Bernshteyn属于这样一群图书管理员，他们对由边连起来的节点——也就是所谓图——的无穷集的相关问题进行整理。特别地，他研究具有无穷多个分离片段的图，而每个片段包含无穷多个节点。大多数图论家并不研究这种类型的图；他们反而聚焦于那些有限的图。可是这种无穷图可以表征并提供关于动力系统和其他重要集合类别的信息，因而成为了描述集合论家感兴趣的一个主要方向。

以下是Bernshteyn和他的同行们可能研究的无穷图类别中的一个例子。从一个圆出发，它包含了无穷多个点。选一个点：这将会是你的第一个节点。接着沿着圆周移动一段固定的距离。这给了你第二个节点。比如，你可以在圆上移动五分之一的距离。在这两个节点间连一条边。移动相同的距离得到第三个节点，并把它与前一个连起来。一次类推。

如果你每次在圆上移动五分之一的距离，经过五步你就回到出发点了。一般而言，如果你移动任何可以写成分数的距离，节点会构成一个闭合的圈。可是如果距离不能写成分数，这一过程会永远持续下去。你会得到无穷数目的连通节点。

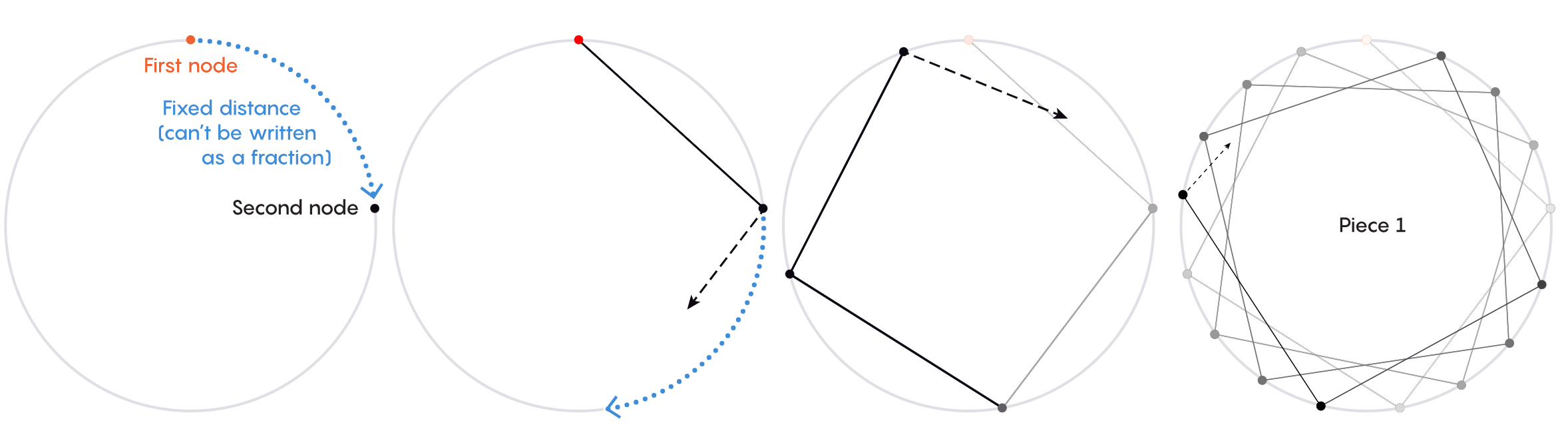
不过这还没完：这一无穷长序列还只是你的图的第一个片段。尽管它包含了无穷多个节点，它并没有囊括圆上的所有点。为了生成图的其它片段，从剩下的那些点之一出发。现在就跟在第一个片段里一样，每一步也移动一段相同的距离。你最终会构建出连通节点的第二个无穷序列，跟第一个完全不连通。

对圆上每一个可能的新出发点执行这一操作。你会得到由无穷多个分离片段构成的图，并且每个片段由无穷多个节点组成。

数学家们接着问，是否可能对这个图的节点着色，使得它们遵循一定的规则。比方说，只使用两种颜色，你是否能对图中的所有节点着色，使得每两个相连的节点不同色？答案可能看起来很直接。从你的图的第一个片段着手，选一个节点，把它着成蓝色。接着对这个片段剩下的节点以一种交替的模式进行着色：黄，蓝，黄，蓝。对你的图的所有片段都执行同样的操作：选一个节点，着成蓝色，接着交替着色。最终，你只需要使用两种颜色就能完成任务。

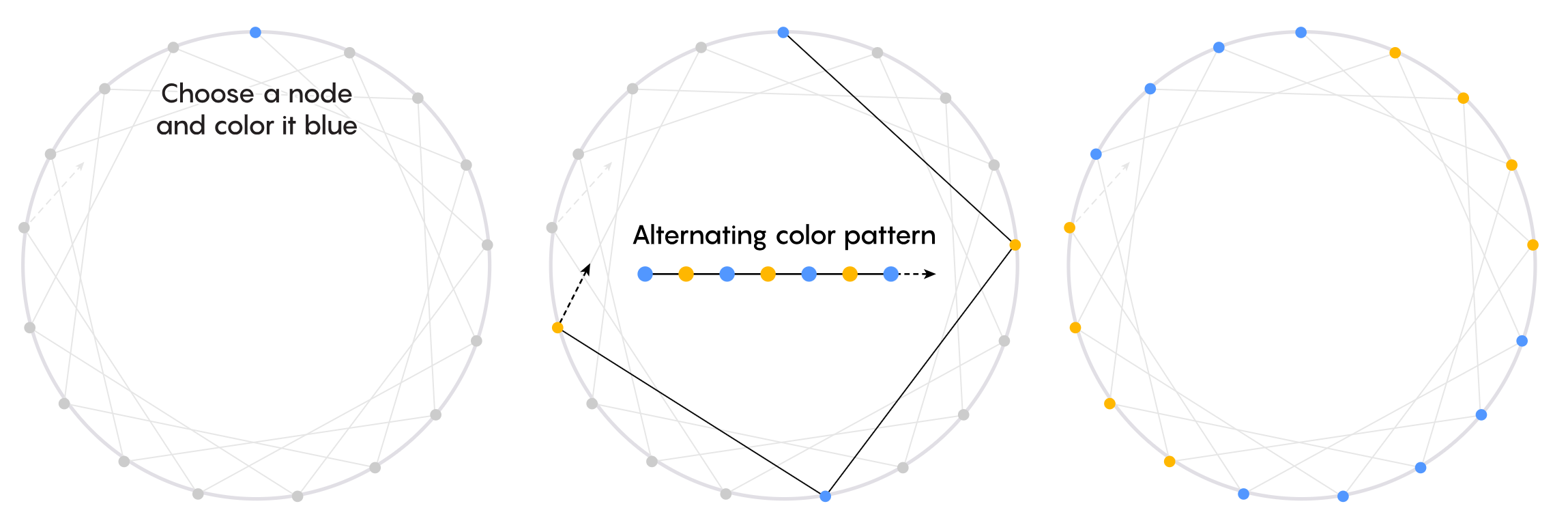
可是为了完成这一着色，你不得不依赖一个隐藏的假定，集合论家们称之为选择公理。它是所有数学命题赖以建立的九大基础构建模块之一。根据这一公理，如果你从一堆集合出发，你可以从这些集合中的每一个选出一个元素来生成一个新集合——哪怕你有无穷多个集合可以进行选取。这一公理是有用的，在于它让数学家得以证明各种各样有意思的命题。不过它也会带来奇怪的悖论。描述集合论家避免使用它。

你的图有无穷多个片段。这对应着无穷多个集合。你从每个集合中选择一个元素——每个片段里你决定着成蓝色的第一个点。所有这些蓝色的点构成一个新集合。你使用了选择公理。

当你接着对剩余的节点以蓝黄交替的模式进行着色时，这会带来一个问题。你对每个节点（它的长度为零）都分别进行了着色，而对来自图的不同片段的节点是如何彼此关联的则一无所知。这意味着你无法用长度来刻画图的所有蓝色节点构成的集合，或者所有黄色节点的集合。换句话说，这些集合是无法度量的。数学家没法对它们给出任何有用的信息。

对于描述集合论家而言，这是不尽如人意的。于是他们想要找到办法来以一种连贯的办法对图着色，这种办法不必使用选择公理，并且给出可测的集合。

为了做到这一点，回顾下你是如何构建你的图的第一个片段的：你在圆上选一个节点，然后将它与一定距离远的第二个节点相连。现在把第一个节点着成蓝色，第二个黄色，并且把它们之间的整段弧着成蓝色。类似地，把第二个和第三个节点间的弧着成黄色。把第三段弧又着成蓝色。以此类推。

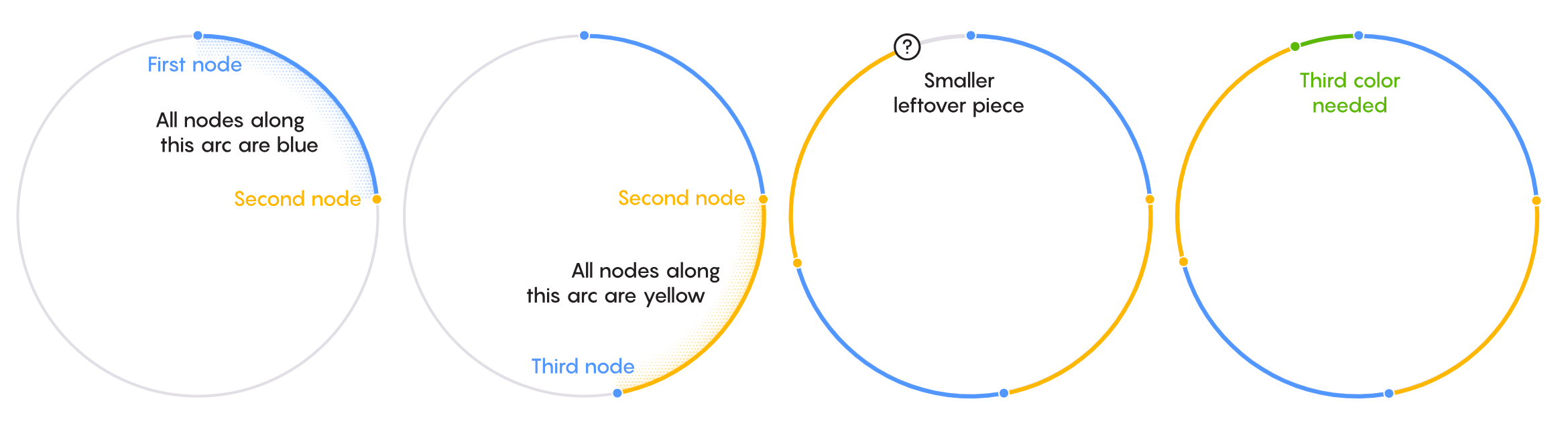
很快，你就对差不多整个圆都完成了——也就是说，除了落在剩下的一小段弧里的节点以外，你对图上的所有其它节点都指派了一种颜色。假定你最后一段弧着的是黄色。那么最终的这一小段弧该如何着色呢？你不能使用蓝色，因为这些节点连着你最初着成蓝色的那段弧里的节点。可你也不能使用黄色，因为这些节点也连回到前一段弧里的那些黄色节点。

你必须使用第三种颜色——比方说，绿色——来完成你的着色。

这样一来，你最终得到的蓝色、黄色和绿色节点全都只是圆周上的弧段，而非你使用选择公理时所得到的散开的点。你可以计算这些集合的长度。它们是可测的。

Bernshteyn研究生的时光就用来研究这种着色问题，把它们一一归类好。接着，在完成学位之后不久，他偶然发现了一种潜在的方法可以将它们一次性地全归类好——并且证明这些问题拥有人们始料未及的、更深刻也更具数学意义的一种结构。

轮番进行

时不时地，Bernshteyn喜欢去听一些计算机科学的报告，而其中的图是有限的，代表着计算机的网络。

2019年，这些报告中的一个改变了他职业生涯的进程。它是关于“分布式算法”的——一堆指令在一个网络中的多台计算机上同时运行，并在没有中央协调器的情况下完成一项任务。

比方说你在一座建筑中有一堆无线网的路由器。相邻的路由器会彼此干扰，如果它们使用相同的通信频道。因此每个路由器需要选择一个与它的紧邻们都不相同的频道。

计算机科学家们会把这重构为图上的一个着色问题：将每个路由器表示为一个节点，并把紧邻用边连起来。仅仅使用两种颜色（代表两种不同的频道），设法对每个节点进行着色，使得每两个紧邻节点的颜色都不相同。

可是有一个问题：节点只能跟它们的紧邻通信，使用所谓的局域算法。首先，每个节点运行一个相同的算法，并为自己指派一种颜色。接着它跟自己的邻居通信，来获知在周围的一个小区域内的其它节点是如何着色的。接下来它再次运行算法，来决定是要保持自己的颜色还是调换它。它会重复这一步骤，直到整个网络获得合理的着色。

计算机科学家想知道一个给定的算法需要多少步骤。例如，任何只用两种颜色就能解决路由器问题的局域算法一定出奇地低效，但如果允许你使用三种颜色，你就可能找到一种非常有效的局域算法。

在Bernshteyn听的那个报告里，报告人讨论了不同种类问题的这些阈值。他意识到，这些阈值之一听起来很像在描述集合论的世界里存在的一个——以一种可测的方式对某些无穷图进行着色所需要的颜色数。

在Bernshteyn看来，这不像只是一个巧合而已。它不仅仅在于，计算机科学家也像是图书管理员，会依照他们算法的运行效率来对问题归类。它也不仅仅在于，这些问题也可以用图和着色来描述。

他觉得，或许这两种书架具有更多的共性。或许这两个领域之间的关联会深刻很多，很多。

或许所有的书以及它们的书架其实都是相同的，只是用了不同的语言来书写——因此需要一个翻译器。

开启大门

Bernshteyn打算揭晓这一关联。他想证明，每一个有效的局域算法都可以转变为一个（满足某些额外重要性质的）无穷图的Lebesgue可测的着色方式。也就是说，计算机科学最重要的书架之一等价于集合论中最重要的书架之一（在等级中地位很高）。

他从那个计算机科学的报告中的网络问题类别开始，聚焦于它们的首要规则——任何给定节点的算法只能使用它的局部邻域的信息，不管图有一千个还是一百万个节点。

为了合理运行，算法所要做的就是对给定邻域内的每一个节点用一个独特的数字来标记，以便它记录近邻节点的信息并对它们发出指令。在有限图中，这很容易做到：只要给图中的每个节点指定一个不同的数字就行了。

计算机科学家Václav Rozhoň已经在利用集合论与网络科学之间新发现的一种关联来解决他自己感兴趣的问题。

如果Bernshteyn可以在无穷图上运行同样的算法，这就意味着他可以用一种可测的方式对图着色——从而解决集合论这一侧的一个图论着色问题。可是这儿有一个问题：这些无穷图的无穷是“不可数”的。没有办法对它们的节点予以独一无二的标记。

Bernshteyn的挑战就在于，要找到一种更巧妙的方法来标记这些图。

他知道必须对标记进行复用。只要近邻节点被差异化标记，这是没问题的。有没有一种办法可以分配标记，使得在同一邻域内没有哪个标记被复用？

Bernshteyn证明这样的办法总是存在的——不管你决定使用多少标记，也不管你的局部邻域内有多少个节点。这意味着，你总可以安全地将计算机科学那边的算法延伸到集合论这边来。“在我们的设定下的每个算法都对应于描述集合论设定下对任意图的一种可测着色方式。” Rozhoň说道。

这一证明让数学家们大吃一惊。它彰显了计算与可定义性，以及算法与可测集合之间的一种深层关联。数学家们如今已在探索如何利用Bernshteyn的发现。例如，在今年发表的一篇文章中，Rozhoň与合作者通过观察计算机科学语境下的同类问题，弄清了如何对所谓树这种特定的图进行着色。这一结果也阐明了哪些工具可以被数学家用来研究树所对应的动力系统。“这是一种非常有趣的经历，试图去证明一个领域内的结果，在那里我甚至不理解基本的定义，” Rozhoň说道。

数学家们也在致力于朝一个方向来翻译问题。在一个实例里，他们使用集合论做出了对解决一类特定问题的难度的全新估计。

Bernshteyn的桥梁不仅仅给出了解决单个问题的一个全新工具包。它还使集合论家们获得了对其领域的一种更清晰的视图。有大量问题他们一直不知道如何分类。在很多情况下，这种局面如今发生了变化，因为集合论家们有了计算机科学家更系统的书架来指引他们。

Bernshteyn希望这一日益壮大的研究方向会改变在职数学家们对集合论家的工作的观念——希望他们不再将其看作是与现实数学世界远离的，互不关联的。“我在努力改变这种观念，”他说，“我想让人们习惯于思考无穷。”

原文链接：

https://www.quantamagazine.org/a-new-bridge-links-the-strange-math-of-infinity-to-computer-science-20251121/