——加速度驱动旋转的几何动力学

一、从一个长期被忽略的事实说起

在传统动力学中，我们习惯这样理解运动：

• 力 → 产生加速度

• 加速度 → 改变速度

• 速度 → 决定轨道

这是一个二阶叙事：因果链条长，计算复杂，且往往要等“算完之后”才能知道结果。

但如果我们退一步，只问一个更靠前的问题：

旋转的节律与强度，究竟由什么决定？

答案并不在“力”，而在加速度场与几何结构本身。

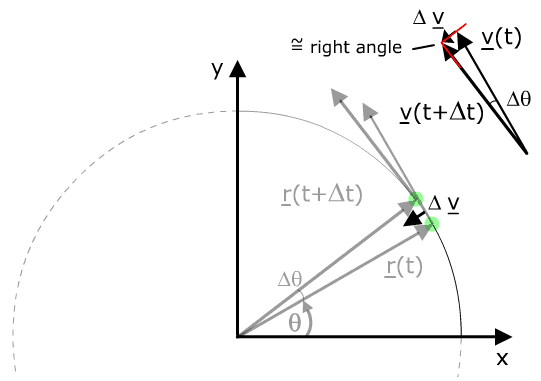
二、柳氏第一公式：节律由加速度给定

                        ω=(L/(GM))g

这条公式可以称为柳氏第一公式。

它的意义并不在于形式，而在于因果方向的改变：

• ω：旋转的角频率（节律）

• L：角动量（几何量）

• GM：系统的尺度常数

• g：加速度场（迦）

这条公式明确表达的是：

旋转的节律不是由“力”推动出来的，而是由加速度场在既定几何尺度上直接规定的。

换句话说：

加速度不再是结果，而是节律的设定者。

这是从二阶动力学，回到一阶几何动力学的关键一步。

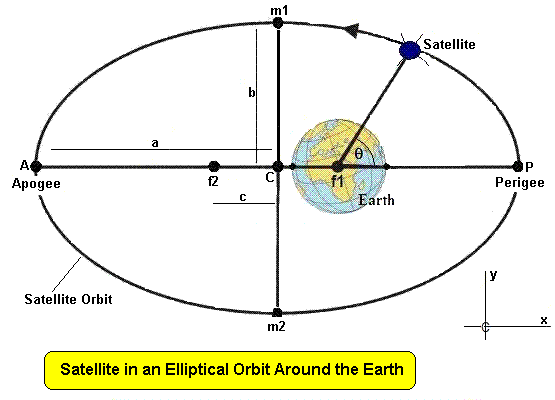
三、柳氏第二公式：速度强度由几何与加速度给定

当运动含纯切向运动速度v时，有：

                        v²=pg,    p=L²/(GM)

这条关系可以称为柳氏第二公式。

它告诉我们的不是“如何计算速度”，而是：

切向速度的强度，并不是由能量积累出来的，而是由“几何尺度 × 加速度场”即时给定的。

在这里：

• p：轨道的几何尺度（半通径）

• g：加速度场

• v：切向速度

速度平方，直接等于几何尺度乘以加速度。

这是一条结构恒等式，而不是推导技巧。

四、两条公式放在一起，世界突然变简单了

把两条柳氏公式并列：

• 柳氏第一公式ω=(L/(GM))g（决定“怎么转”）

• 柳氏第二公式v²=pg （决定“转多快”）

你会发现一个非常干净的事实：

旋转运动的节律与强度，完全由可测的加速度场 g和可测的几何量 L,p 决定。

在这两条公式中：

• 力不再是核心变量

• 能量不再是因果起点

• 二阶微分方程自然退场

剩下的，只有加速度场 + 几何。

五、这不是抽象理论，而是工程入口

柳氏第一、第二公式的真正价值，在于它们：

• 只依赖可测量

• 可以即时校验

• 可以反向设计

例如：

• 测得 g，立刻知道系统的旋转节律 ω

• 测得 g，立刻知道允许的速度强度 v

• 不满足 v²=pg，说明结构假设本身就错了

这使得复杂系统第一次可以：

在计算之前判断，在实验之前筛选，在设计阶段就排除结构性失败。

六、一种不同的动力学世界观

柳氏两条公式所代表的，并不是“多一组公式”，而是：

一种新的动力学叙事方式。

• 世界不是被力推着走

• 旋转不是力的结果

• 运动的基本节律，由加速度场在几何中直接表达

这正是“一阶、无力、可设计”的动力学观。

七、结语

文明不相信眼泪，但相信能够被反复使用的定律。

柳氏第一与第二公式的目标，并不是解释一切，而是把能够讲清楚的那一层，讲到不能再清楚。

至于更复杂的部分，留给时间，留给工程，留给后来的人。

我已经把该说清楚的，说清楚了。