计算机科学里程碑式的证明波及物理与数学

计算机科学家们在可计算式验证的知识方面拓展了新的疆域。在此过程中，他们解决了量子力学与纯数学中的重大未解难题。

Kevin Harnett 著

左   芬     译

【译者按：在过去几年里，量子信息领域出现了两次重大突破。其一，通过对基于扩展图的经典LDPC码进行巧妙的乘积操作，得到了性能良好的量子LDPC码，并在此过程中解决了经典编码中的c³猜想。好的量子LDPC码的出现极有可能改变量子计算机硬件路线的当前格局，并将对量子物质相的研究产生深远影响。关于（量子）LDPC码的内容我们在前面的译文中已经陆续介绍过。

其二，在Bell实验基础上发展起来的“非定域游戏”被引入到复杂度理论的交互式证明中，并极大地拓展了多方交互式可验证问题的范围。简而言之，在量子纠缠的辅助下，我们现在甚至能验证停机问题！相信Turing若重生，也会对此惊讶不已。在此过程中，物理学中关于纠缠模型的Tsirelson论断与数学中关于算子代数的Connes嵌入猜想被否定。

这篇文章介绍了量子纠缠是如何大幅提升交互式证明的能力的。在此翻译出来，供大家参考。原文2020年4月8日刊载于QuantaMagazine，链接见文末。】

计算机科学中的一个新证明也影响了量子力学和纯数学的研究者。

1935年，Albert Einstein与Boris Podolsky、Nathan Rosen共同提出了由量子物理的新定律揭示的一种可能性：两个粒子无论相隔多远，也能相互纠缠或者关联。

就在第二年，Alan Turing首次表述了计算的一般性理论，并证明存在计算机永远无法解决的问题。

“这两种思想来自同一时期。它们以这种戏剧性的方式再次一同回归真的是太棒了。”

                                —— Henry Yuen, 多伦多大学

这两种思想革新了它们各自的领域。看起来它们彼此毫不相干。但如今一个里程碑式的证明将它们结合在一起，同时解决了计算机科学，物理与数学中的大量未解难题。

新证明证实，使用纠缠量子比特/量子位，而不是经典的1和0，进行计算的量子计算机理论上可以用于验证极其庞大的问题集合的答案。纠缠与计算之间的对应震惊了众多研究者。

“完全出人意料，”在维也纳市量子光学与量子信息研究所研究量子物理的Miguel Navascués称。

该证明的作者们最初想要确定一种方法在验证计算类问题的答案上的极限。这种方法涉及了纠缠。通过找出这一极限，他们最终还附带式地解决了另外两个问题：物理中关于如何数学建模纠缠的Tsirelson难题，以及纯数学中被称为Connes嵌入猜想的相关问题。

最终，结果像多米诺骨牌一般倾泻而下。

“这两种思想来自同一时期。它们以这种戏剧性的方式再次一同回归真的是太棒了。”证明的作者之一，多伦多大学的Henry Yuen说道。共同作者还包括悉尼科技大学的季铮锋，加州理工学院的Anand Natarajan与Thomas Vidick，以及德州大学奥斯汀分校的John Wright。五位研究者全都是计算机科学家。

不可判定问题

“你等了一百万年，程序还没终止。是不是得等到两百万年呢？这可不好说。”

                      —— William Slofstra, 滑铁卢大学

在计算机真正出现之前，Turing就定义了关于计算的基本框架。与此同时，他说明存在某种问题，可以证明计算机是无法处理的。这跟一个程序是否会终止有关。

通常地，计算机程序接收输入，并产生输出。但有些时候，它们陷入了无限循环，永不停歇地运行着。如果发生了这种事，就只能关机了。

“你只能手动终止程序。把它关掉，”Yuen说。

Turing证明，不存在万能算法可以判定一个程序会终止还是会永远运行下去。你只能运行程序来查明。

计算机科学家Henry Yuen，Thomas Vidick，季铮锋，Anand Natarajan与John Wright共同完成了关于验证计算类问题答案的一个证明，并最终解决了数学和量子物理中的重大问题。

“你等了一百万年，程序还没终止。是不是得等到两百万年呢？这可不好说，”滑铁卢大学数学家Willian Slofstra说。

用术语来说，Turing证明了这一停机问题是不可判定的——哪怕用你能想象出来的最强大的计算机也无法解决它。

在Turing之后，计算机科学家开始按困难程度分类其它问题。更难的问题需要更多的计算资源去解决——更多的运行时间，更多的存储。这就是计算复杂度的研究内容。

最终，每一个难题都带来两个问题：“求解它有多难？”以及“验证一个答案是对的有多难？”

讯问式验证

当问题相对简单时，你可以自己检验答案。可当它们越来越复杂时，哪怕检验答案也变得不堪重负。不过，计算机科学家们在1985年意识到，哪怕你不能自己确认，仍可以就一个答案的正确性建立信心。

这一方法遵循了警察的讯问逻辑。

如果嫌疑人编造了一个精巧的故事，可能你无法在现实中确认每一个细节。但通过问适当的问题，你可以揪出嫌疑人的谎言，或者对故事属实建立信心。

用计算机科学术语来说，讯问中的两方分别是给出问题答案的强力计算机，也就是证明者，与想要通过问证明者问题来判定答案是否正确的不那么强大的计算机。第二台计算机被称为验证者。

举一个简单的例子，假设你是色盲，而另一个人——证明者——声称两颗弹珠具有不同颜色。你没法自己检验这一论断，但通过巧妙的讯问还是可以判定它是否是真的。

把两颗弹珠放到背后，混起来。接着拿出来让证明者告诉你是哪颗。如果它们颜色不同，证明者每次都能给出正确答案。如果弹珠其实颜色相同——意味着它们看起来完全一样——证明者有一半的时候会猜错。

“如果我发现你在远远超过一半的时候对了，我相当确定它们是不同的”颜色，Vidick说道。

通过问适当的问题，你可以验证一大类问题的答案，远远超过亲自动手的。

1988年，计算机科学家开始考虑如果两个证明者给出同一问题的答案会发生什么。毕竟，如果你有两个嫌疑人可以讯问，查清一桩案子或者验证一个答案总归容易得多，因为你可以让他们相互对抗。

“它给予了验证者更多手段。你分别讯问，问相关联的问题，然后交叉验证答案。”Vidick说道。如果嫌疑人说的是实话，他们的回答大多数时候都会是一致的。可如果他们说谎，答案会经常相悖。

类似地，研究者证明，通过分别讯问两个证明者，你可以快速验证

更大类别问题的答案，比你只有一个证明者可以讯问时大得多。

计算复杂度可能看起来完全是理论上的，但它也跟现实世界紧密相关。计算机用来求解和验证问题的资源——时间和存储——在根本上是物理的。基于这一原因，物理学上的新发现会改变计算复杂度。

“如果你选择不同层次的物理，比如用量子的替代经典的，你会从中得出不同的复杂度理论，”Natarajan说道。

新证明正是21世纪计算机科学家们在直面20世纪物理学最奇怪的概念之一——纠缠——后的最终结果。

Connes嵌入猜想

当两个粒子纠缠时，它们其实并不相互影响——它们没有因果关联。Einstein和他的合作者在他们1935年的文章里阐明了这一思想。之后，物理学家和数学家们试图找到一个数学方法来刻画纠缠的真实涵义。

可是这一努力带来的结果有些混乱。科学家们提出了纠缠的两种不同数学模型——并且不清楚它们是否彼此等价。

以一种迂回的方式，这一潜在的不和谐后来引发了纯数学中被称为Connes嵌入猜想的一个重要问题。最终，它也成为了五位科学家在他们的新证明中加以利用的突破口。

一种建模纠缠的方法是把粒子想象成在空间上相互远离。比如说，一个在地球上，而另一个在火星上；它们之间的距离阻止了因果性。这被称为张量积模型。

可在有些情形下，两样事物是否彼此因果性远离并不十分明显。于是数学家们想出了第二种更一般地描述因果独立性的方法。

当你执行两个操作的顺序不影响结果时，这些操作“可对易”：3×2跟2×3一样。在这第二种模型里，说两个粒子是纠缠的，如果它们的性质相互关联并且与你执行测量的顺序无关。测量粒子A来预言粒子B的动量或者反过来，无论哪种方式，结果都一样。这被称为纠缠的对易算符模型。

两种纠缠的描述都使用了排成行和列的数组，也就是矩阵。张量积模型使用了只有有限行和列的矩阵。对易算符模型使用了一种更一般的对象，运作起来像是具有无限行和列的矩阵。

随着时间的推移，数学家们开始从他们自身的兴趣出发来研究这些矩阵，完全不考虑跟物理世界的任何关联。作为这类工作的一部分，数学家Alain Connes1976年猜想应该可以用有限维矩阵来近似很多无限维矩阵。这是Connes嵌入猜想的推论之一。

在之后的十年里，一个名叫Boris Tsirelson的物理学家给出了这一问题的另一个版本，让它重新扎根于物理学之中。Tsirelson猜想纠缠的张量积和对易算符模型大体上应该是等价的。这是说得通的，因为理论上它们是描述同一种物理现象的两种不同方式。后续的工作表明出于矩阵和使用它们的物理模型之间的这种关联，Connes嵌入猜想和Tsirelson问题彼此蕴涵：解决了一个，你就解决了另一个。

然而两个问题的答案最终全都出现在了另一个地方。

游戏物理

1960年代，一个名叫John Bell的物理学家想到了一个测试，可以用来判定纠缠到底是一种真实物理现象，还是仅仅是一个理论概念。这一测试涉及一种游戏，其输出会揭示是否有超出常规非量子物理的某种东西在起作用。

计算机科学家后来意识到这一纠缠测试也可以作为工具来验证极其复杂问题的答案。

为了看出这些游戏如何运作的，首先我们给定两个玩家，Alice和Bob，以及一个3乘3的网格。一个裁判给Alice某一行，让她在每个格子里填0或1，使得数字加和是一个奇数。Bob则被指定了某一列，并且要让填的数字加起来是一个偶数。如果他们在行和列相交的格子里填了相同的数字，则获胜。但他们不允许交流。

在通常情形下，他们最多能有89%的机会获胜。但在量子情形下，他们可以做得更好。

假定Alice和Bob分享了一对纠缠粒子。他们对各自的粒子进行测量，并用结果来确定每个格子里该填1还是0。因为粒子是纠缠的，他们的测量结果也会是关联的，这意味着他们的答案也相关——也就意味着他们能100%赢得游戏。

量子游戏

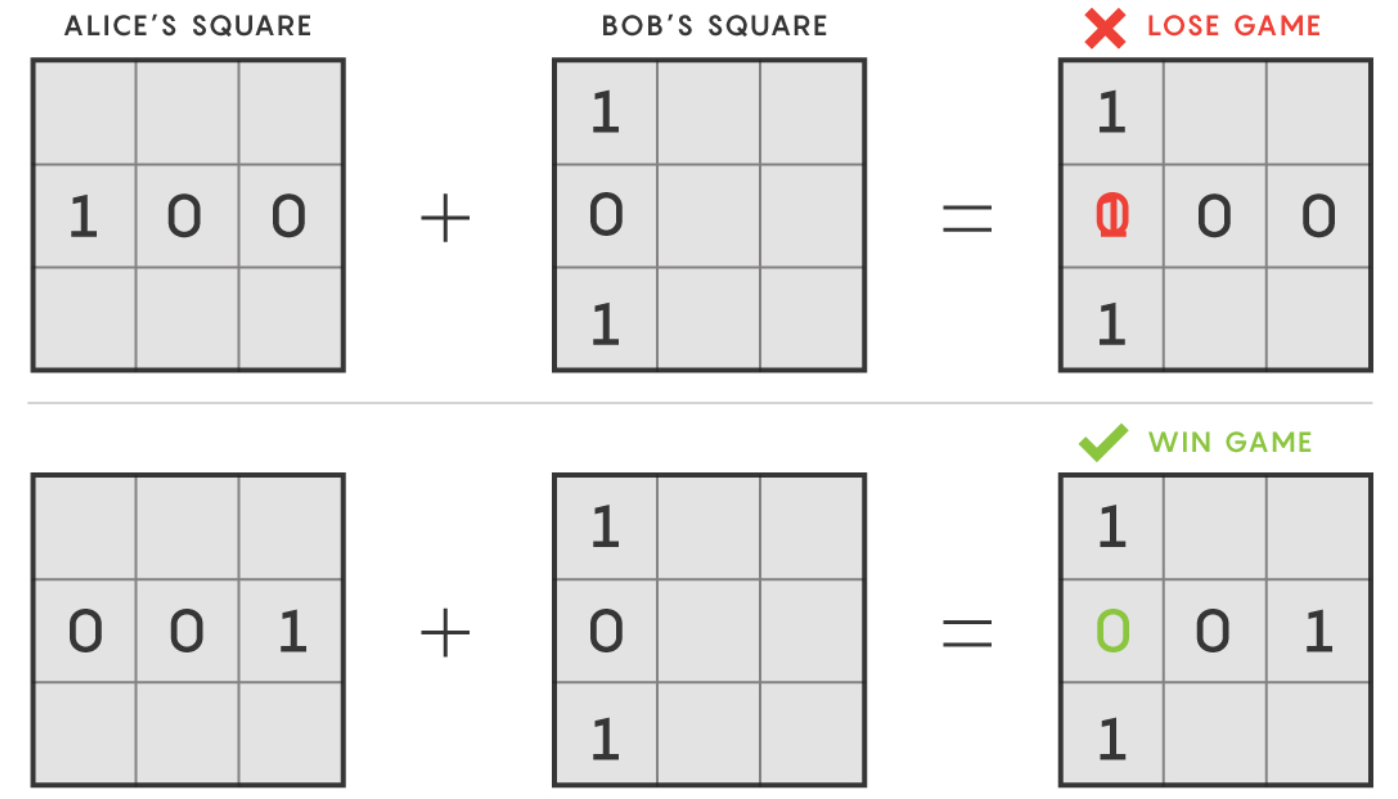
要点：两个玩家都不知晓被分配了哪一行或者哪一列。

因此如果你看到两个玩家以出奇高的频率赢得游戏，就可以断定他们利用了某种超出经典物理的东西。这种Bell-类型的实验现在被叫做“非定域”游戏，意指两个玩家是相互分离的。事实上物理学家们已经在实验室里实现了它们。

“人们已经进行这种实验好多年了，结果表明这种幽灵般的东西是真实存在的，”Yuen说。

就跟分析其它任何游戏一样，你可能也想知道玩家能有多大概率赢得非定域游戏，如果他们玩到最佳的话。例如，对于单人跳棋，你可以算出完美玩家有多大概率会赢。

可是在2016年，William Slofstra证明，不存在通用算法可以算出所有非定域游戏的准确最大获胜概率。于是研究者们琢磨：是不是可以至少算出近似的最大获胜百分比？

计算机科学家们聚焦于使用两种描述纠缠的模型得到的答案上。使用张量积模型的一种算法确定了所有非定域游戏的近似最大获胜概率的一个下限，或者说最小值。而使用对易算符模型的另一种算法确定了一个上限。

这些算法运行得越久，给出的答案就越精确。如果Tsirelson的预言是对的，两个模型确实是等价的，那么下限和上限就会持续彼此靠近，最终汇合到近似最大获胜百分比的单一数值上。

但如果Tsirelson的预言是错的，两个模型并不等价，“上限和下限始终会是分离的，”Yuen说。那就没有什么办法来计算非定域游戏的哪怕近似的获胜百分比。

在他们的新工作中，五位研究者使用这一问题——关于上限和下限是否会汇合以及Tsirelson问题是对还是错——来解决一个不相关的问题，也就是何时可以验证一个计算性难题的答案。

纠缠助手

2020年代早期，计算机科学家们开始琢磨：如果你讯问两个共享纠缠粒子的证明者，能够验证的问题的范围会发生什么变化？

大多数人认为纠缠与验证是相悖的。毕竟，如果两个嫌疑人有某种方法可以协调他们的答案，会更容易编造一致的谎言。

但在过去几年里，计算机科学家们意识到情况恰好相反：通过询问共享纠缠粒子的证明者，你可以验证比没有纠缠时大得多的问题类别。

“纠缠是一种产生关联的方式，你可能觉得会有利于他们说谎或者作弊，”Vidick说道，“但事实上你也可以把它用到对你有利的一面。”

要理解这是为何，你首先得领会到，通过这种交互式过程能验证的问题的规模可以说是非比寻常的。

想象一个图——由线（边）连接的点（顶点）的集体。你想要知道是否可以用三种颜色对顶点进行着色，使得任意一条边连接的顶点颜色都不相同。如果你能做到，我们就说这个图“可以三着色”。

如果你交给两个纠缠着的证明者一个非常大的图，而他们答复说它可以三着色，你会好奇：是否有办法验证他们的答案呢？

对于很大的图，是不可能直接检验结果的。因此取而代之，你让每个证明者告诉你相连的一对顶点之一的颜色。如果他们报告两种不同的颜色，并且他们每次都能保持这样，你会信服三着色确实可行。

但哪怕这种讯问策略也会失效，如果图非常大——拥有比宇宙中的原子数目还多的边和顶点。这时哪怕陈述一个特定问题（“告诉我XYZ顶点的颜色”）这一任务也超出了作为验证者的你的能力范围：命名一个特定顶点的数据量超出了你的工作内存的容量。

但是纠缠使得我们可以让证明者自己提出问题。

“验证者无需计算出问题。验证者迫使证明者自己计算出问题，”Wright说。

验证者希望证明者报告相连顶点的颜色。如果顶点并不相连，那么答案对于图是否已经三着色起不到什么作用。换句话说，验证者想让证明者提出相关联的问题：一个证明者问顶点ABC，另一个问顶点XYZ。我们希望这两个顶点是彼此相连的，哪怕两个证明者都不知道另一个考虑的是哪个顶点。（正如Alice和Bob想要在同一个方格里填相同的数字一样，尽管他们都不知晓另一个人被问的是哪一行或者哪一列。）

如果两个证明者完全独立地提出这些问题，就没有办法迫使他们选择相连的，或者说关联的顶点，好让验证者核实他们的答案了。而这种关联性恰好是纠缠能赋予的。

“我们会利用纠缠把几乎所有事情都卸载到证明者那里。我们让他们自行选择问题，”Vidick说道。

在这一过程的最后，证明者各自报告一个颜色。验证者检验它们是否相同。如果图确实是可三着色的，证明者永远不会报告相同的颜色。

“如果存在一种三着色，证明者总能让你信服，”Yuen说。

结果表明，这一验证过程是非定域游戏的另一个实例。如果证明者让你信服他们的答案是对的，就“获胜”。

2012年，Vidick和Tsuyoshi证明，让纠缠证明者参与多种多样的非定域游戏可以验证的问题数目至少跟讯问两台经典计算机一样多。也就是说，采用纠缠证明者并不与验证相悖。而去年，Natarajan和Wright证明，与纠缠证明者交互实际上扩展了可以验证的问题类别。

但计算机科学家仍不知晓以这种方式能够验证的问题的完整范围。现在不同了。

推论如注

“这类模型的验证能力简直难以置信。”

                              ——Henry Yuen, 多伦多大学

在他们的新文章中，五位计算机科学家证明，讯问纠缠证明者可以验证包括停机问题在内的不可解问题的答案。

“这类模型的验证能力简直难以置信，”Yuen说。

可是停机问题是无法求解的。而这一事实正是引发最终证明的导火索。

假定你把一个程序交给一对纠缠证明者。你让他们告诉你程序是否会终止。你打算通过一种非定域游戏来验证他们的答案：证明者生成问题并作答，如果他们的答案一致就“获胜”。

如果程序确实终止，证明者会100%赢得这个游戏——类似于图的三着色，纠缠证明者永远不会对相连的两个顶点报告相同的颜色。如果它不终止，证明者只能靠运气获胜——只有50%的机会。

这意味着，如果某人让你确定这一非定域游戏的一个特定实例的近似最大获胜概率，你首先得解决停机问题。但停机问题是无法解决的。这意味着计算非定域游戏的近似最大获胜概率是不可判定的，正如停机问题。

而这反过来又意味着Tsirerlson问题的答案是否定的——纠缠的两种模型是不等价的。因为如果它们等价，你可以把上限和下限汇合到一起来计算出一个近似最大获胜概率。

“不可能有这样一种算法，所以这两种【模型】必然是不同的，”马德里市康普顿斯大学的David Pérez-García说道。

这篇新文章证明，通过与纠缠的量子证明者交互能验证的问题类别，所谓MIP^*类，跟难度不超过停机问题的一类问题，所谓RE类，是刚好一样的。文章的标题简洁地表述了这一点：“MIP^*=RE”。

在证明这两种复杂度类别相等的过程中，计算机科学家们也就证明了Tsirelson问题的答案是否定的。结合此前的一些工作，这也意味着Connes嵌入猜想是错的。

对于这些领域的研究者来说，如此重大问题的答案居然出现在计算机科学中看起来毫无关联的一个证明中 ，简直是石破天惊。

“如果我看到一篇文章标题是MIP^*=RE，我不会认为它跟我的工作有任何关系，” 之前参与到将Tsirelson问题与Connes嵌入猜想联系到一起的工作中的Navascués说，“这完全出乎我的意料之外。”

量子物理学家和数学家还刚开始消化这一证明。在这一新工作之前，数学家们曾琢磨是否可以摆脱对无穷维矩阵的近似，转而使用大的有限维矩阵。现在，因为Connes嵌入猜想是错的，他们知道行不通了。

“他们的结果意味着这是不可能的，”Slofstra说道。

计算机科学家们自己并不打算去解决Connes嵌入猜想。因此，他们没法作为最佳人选去解释他们其实已经解决了的这一问题的后续影响。

“从个人角度来说，我并不是一个数学家。我不是太理解Connes嵌入猜想的原始表述。”Natarajan说。

他和他的合作者预计数学家们会把这一新结果翻译成他们自己领域的语言。在公布证明的一篇博客推送中，Vidick写道，“我毫不怀疑最终不需要复杂度理论也能获得这些纯数学结论。”

而在其他研究者利用这一证明的同时，导向它的一系列探寻也将要终止了。在过去三十多年里，计算机科学家们竭力弄清交互式证明能把他们带到多远。他们现在看到了答案，在简短标题下带着Turng回声的一篇长文里。

“这一长系列的工作只是好奇”两个纠缠的量子证明者的验证过程“能有多强大”，Natarajan说道，“现在我们知晓了它的威力。这一故事也将终结。”

原文链接：

https://www.quantamagazine.org/landmark-computer-science-proof-cascades-through-physics-and-math-20200304/