博文
行列式的行和列为什么与传统辞典上的解释不同
||
行列式的行和列为什么与传统辞典上的解释不同
对于理工科出身的人,提起行和列,几乎像条件反射一样的立刻会想到行列式。从中学开始解二元一次方程组和三元一次方程组中引出的行列式解法,到量子力学中表示原子-分子状态的斯雷特行列式,矩阵的行和列以及方阵的行列式会始终跟随着大多数的理工科人。
矩阵和行列式的行是指横着一排,列则是指竖着的一排。
但是,在传统的汉语语境中,行和列的说法,却正好与我们在现代数学中学到的相反。看看两种传统权威词典上的解释:《辞源》这样说:“行列,排列的次第。直的叫行,横的叫列。”《中文大辞典》这样说:“行列,謂列之次第也。凡排比多数之次第,直者曰行,横者曰列。”其他词典上也都是这样说的。
举一个例子,我们传统的书籍,从竹简到纸本书,文字都是竖排的,横排的书籍是近现代的产物。成语“一目十行”,出自唐初姚察、姚思廉撰的《梁书》,说简文帝“读书十行俱下”。一下子看了十行字,虽然是夸张,但是显然这里的行是直的,从上到下,因为那时候没有横排的书。比这更早一点,南朝范晔编撰的《后汉书·应奉传》说:“(应)奉读书,五行并下。”这里倒没有说他一下子看十行,但是也看了五行。不管是五行还是十行,都是“俱下”或“并下”,从上往下看。
为什么传统的行是竖直的而不是横的呢?
行的本义是“步趋”,也就是今天所说的走路。《说文解字》:“行,人步趨也。从彳从亍。《韵会》这样解释:“从彳,左步。从亍,右步也。左右步俱举,而后为行者也。”
人们走路,大多一个人跟着一个人,排列成行。如果一群人走路不是一个挨一个所谓鱼贯而行,而是横排着走,那就太不像话,别人没办法走路,对面的人也过不来了。
行又是道路的意思,行路,引申为通行,无论是人还是水即河流的流动,都是前后一线的通行。
辈行,是按辈分的大小排列。弟兄的排行,是按年龄的大小排列。
即使后世作量词,如“两行热泪”,也都是竖的不是横的。
所以,传统上的行是直排,不是横排。运动着的行,是一个跟着一个的前进,不是齐头并进。
列是分解、分裂的意思,就是把物体分开来,引申为排列。
《荀子》:“古者列地建国”,这里的列地就是分地、裂地,即所谓分封诸侯。裂是把布帛分开而可以做衣服。后来人们写分裂,用裂字把列的本义取代了。而列则主要用于它的引申义排列。
成语“列鼎而食”出自西汉刘向的《说苑》:“累茵而坐,列鼎而食。”说天子或诸侯这些贵族“列鼎而食”,那就是吃饭时面前排列盛着食物的鼎,这些鼎显然都是横排的,纵排将难以取食。西汉初的晁错《论贵粟疏》中说:“商贾……小者坐列贩卖”。这里小贩们的“坐列贩卖”,如今我们都还能见到,都是一字排开,只有横排,没有纵排的道理。陈列,罗列,都是横排在人们面前,以便于观看。
当然,说行是直排,列是横排往往是在行与列相对时这样用。在很多情况下,即单独说行或列时,往往行与列都可以用,在这种情况下,人们常常说行就是列,列就是行,二者不分。
总之,在传统上,行列相对时,行是纵的,列是横的。跟如今矩阵、行列式中间的行和列正好是反的。对于这一点,在我们需要要弄清楚,不然我们学理工科的人只囿于我们在数学上的知识,遇到传统的语言,往往会感到困惑。
那么,为什么现在矩阵和行列式中的行和列的说法会与传统行列的用法不同呢?
这个问题还需要从头说起。行列式最早是从解一次方程组(即线性方程组)开始的。方程这个名词是中国古代就有的,有着非常久远的历史。方程原来是指解线性方程组的过程中形成的一些数字的表格,也指解线性方程组的一种方法。方,矩形;程,程式。差不多两千年前,汉代的《九章算术》的第八卷就取名曰“方程”。该卷一开始就给出了一道三元一次方程组的算题,翻译成白话文如下:
今有上等黍3捆、中等黍2捆、下等黍1捆,打出的黍子共39斗;上等黍2捆、中等黍3捆、下等黍1捆,打出的黍子有34斗;而上等黍1捆、中等黍2捆、下等黍3捆,打出的黍子则有26斗。问每一捆上等黍、中等黍和下等黍各能打出多少斗黍子?
显然,任何没有把初中代数全部忘记的人,都很容易写出如下的三元一次方程组
3x + 2y + z = 39
2x + 3y + z = 34
x + 2y + 3z = 26
用加减法很容易解出这个方程组。但是,在《九章算术》中自然不会有xyz这些变量名,在计算时它们实际上也没有什么用处,只要人们记住它们的相对位置即可,如我们可以这样写
3 2 1 39
2 3 1 34
1 2 3 26
这是一个三行四列的矩阵,前面的三列,可以构成方程的系数行列式。方程组的加减法在这里就表现为对数表中数目的加减。
当然,《九章算术》中也不会有阿拉伯数字,书中的“表格”根据中国人写文章的传统习惯,数字是从上而下竖着排列的,列序则是从右到左,这样就给出了下面这样的“方程”。
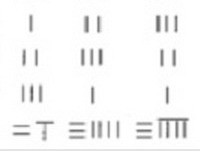
用传统的说法,上面的“方程”从右往左总共三行,每行四个数字。显然,上面阿拉伯数字阵列的第一“行”相当于《九章算术》中表的最右边的竖看的一行,第二“行”相当于“方程”中间的一竖行,第三“行”就是最左边的一竖行。也就是说,现代矩阵和行列式是把古代的“方程”横过来了,从“竖排本”变成了“横排本”,而行和列的名称并没有变。
在竖排转变为横排的过程中,行与列的形式已经变化了,但是它们的名称没有变化。这样做的结果,就引出了对行、列理解的歧义。
这就是如今矩阵和行列式中的行和列与传统语境中行和列表述不同的来历。
我记得有一位物理学家曾经叹息我们的前辈没有把西语的determinant翻译成“决定式”或“确定式”,而是翻译成行列式,从而影响了对determinant这个词意义的理解。其实,也正是我们古代已经有现成的由“行和列”组成的表格,才使我们的先辈把determinant根据其形式翻译成行列式,而不是根据其意义翻译为确定式。
与由于竖排转变为横排致使行列式中行和列的“形式”发生变化一样,书籍印刷的竖排转变为横排,也使得书籍中的文字由古代的从上到下成一行,转变为现代的从左往右成一行;从古代的行从右往左排列,转变为现代的行从上到下排列。
古人的“一目十行”是看竖着的十行,今人的“一目十行”则是看横着的十行。同样的一目十行,一字不变,这里行的“形式”却不同了。
弄清楚了事情的来龙去脉,我们就能够理解现代数学中矩阵与行列式的行、列与传统词典上的表述为什么如此不相同,而不至于惊讶于为什么会产生这样的不同了。
https://blog.sciencenet.cn/blog-612874-1385537.html
上一篇:利用科技进步改革研究生招生办法
下一篇:从留级说教育的实事求是
全部作者的精选博文
- • 灶与炉
- • 教育不是竞赛
- • 化与花
- • 量与物理量
- • 姓名与学术著作的署名
- • 人类的知识与个人的知识
全部作者的其他最新博文
- • 灶与炉
- • 教育不是竞赛
- • 化与花
- • 应当重视有关当代事物的记录
- • 量与物理量
- • 姓名与学术著作的署名