博文
刊·见 | 与 Applied Mathematics in Science and Engineering一起探索数学  精选
精选
||
伽利略说:“ 给我空间、时间以及对数,我就可以创造一个宇宙。”
华罗庚说:“ 宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。”
达芬奇说: “ 在科学中,凡是用不上任何一种数学的地方,凡是和数学没有联系的地方,都是不可靠的。”
马克思说: “一门科学,只有当它成功地运用数学时,才能达到真正完善的地步。”
本期刊·见为诸位介绍应用数学领域期刊 Applied Mathematics in Science and Engineering(AMSE)。除了对期刊进行详尽的介绍外,还向您介绍刊内近三年高被引文章,以及近一年高阅读量文章:
l在高阶伪双曲问题中确定时变位势
l基于扰动观测器的非线性系统模糊自适应最优有限时间控制
l农民意识下咖啡果螟虫害的优化控制分析

Applied Mathematics in Science and Engineering(AMSE)发表所有与数学方法有关的高水平研究,包括其在生物学、医学、金融学、经济学、计算机科学、物理学和工程学等不同领域的应用。期刊涉及的主题包括但不限于:
l微分方程(如常微分方程、偏微分方程、脉冲微分方程、分数阶微分方程、延迟微分方程、泛函微分方程等)
l差分方程、动态方程、动力系统
l积分方程
l控制和优化
l逆问题
l科学计算和数值分析
l计算数学和数据科学
该期刊已被SCI、SCIE、Scopus、CAS、EBSCO、Google Scholar等数据库收录。

2022影响因子:1.3
2022 5年影响因子:1.3
2022 CiteScore: 3.4
2022CiteScore最佳分区: Q2
年下载量:19万次
稿件接受率:35%
影响因子排名
根据JCR显示,Applied Mathematics in Science and Engineering在
· 工程,多学科领域排名:76/178
· 数学,跨学科应用领域排名:84/134
CiteScore
根据Scopus显示, Applied Mathematics in Science and Engineering 的
· CiteScore(2022)为 3.4
· CiteScoreTracker(2023)为 3.7
在数学:应用数学领域排名171/609
在工程学:普通工程学领域排名103/302
在计算机科学:计算机科学应用 384/792
编辑团队
Applied Mathematics in Science and Engineering 的主编由来自美国密苏里科技大学的Martin Bohner教授担任,编委团队由多国学者组成。其中,来自中国的是山东大学李同兴教授。
主编介绍

Martin Bohner,美国密苏里科技大学数学与统计学系校董会杰出教授。他的研究方向集中在微分方程、差分方程和动态方程及其在经济学、金融学、生物学、物理学和工程学中的应用。
中国编委介绍
李同兴,山东大学控制科学与工程学院教授,齐鲁青年学者,教育部学科(控制科学与工程)评估专家。他的研究方向为:动态方程定性理论与应用。
作者分布
根据JCR显示,近三年在Applied Mathematics in Science and Engineering发文的国家中,发文排名前三位的国家有:
· 中国
· 美国
· 伊朗
近三年,在Applied Mathematics in Science and Engineering发文的全球高校和科研机构中,发文排名前三位的是:
· 印度理工学院系统
· 中国科学院
· 俄罗斯科学院
近三年内高被引文章

Determination of a time-dependent potential in the higher-order pseudo-hyperbolic problem
在高阶伪双曲问题中确定时变位势
作者:M. J. Huntul
摘要:
The scope of this paper is to determine the time-dependent potential term numerically in the fourth-order pseudo-hyperbolic equation with initial and boundary conditions from an additional measurement condition. From the literature, we already know that this inverse problem has a unique solution. However, the problem is still ill-posed by being unstable to noise in the input data. For the numerical realization, we apply the Crank–Nicolson finite difference method combined with the Tikhonov regularization to find a stable and accurate numerical solution. The resulting nonlinear minimization problem is solved computationally using the MATLAB routine lsqnonlin. Both exact and numerically simulated noisy input data are inverted. Numerical results presented for two examples show the efficiency of the computational method and the accuracy and stability of the numerical solution even in the presence of noise in the input data.
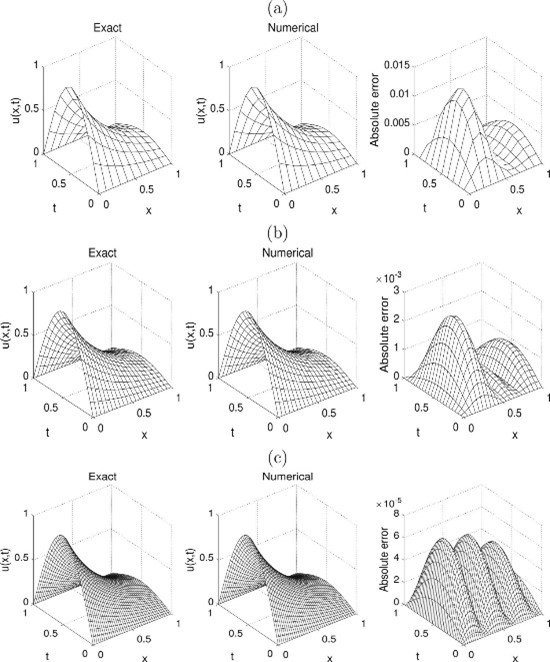
The exact (Equation21) and numerical solutions for u(x,t), with various grid sizes M = N for: (a) 10, (b) 20 and (c) 40, for direct problem. The absolute error between them is also included.
近一年内高阅读量文章

Disturbance observer-based fuzzy adaptive optimal finite-time control for nonlinear systems
基于扰动观测器的非线性系统模糊自适应最优有限时间控制
作者:Zidong Sun et al.
摘要:
This paper investigates the issue of disturbance observer-based fuzzy adaptive optimal finite-time control in light of the backstepping approach for strict-feedback nonlinear systems with bias fault term and full state constraints. Considering that external disturbance and bias fault signal can affect the stability of control and control quality, a disturbance observer is constructed to track the external disturbances and bias fault online. A disturbance observer-based finite-time control strategy is proposed to achieve optimized control by utilizing the fuzzy logic system approximation-based adaptive dynamic programming method under the critic-actor framework. The purpose of the critic is to evaluate control performance and the role of the actor is to execute control behaviour. In addition, it is proved that the proposed fuzzy adaptive optimal finite-time scheme not only realizes all signals in closed-loop system are bounded, but also ensures that system states are restricted within specific sets. Finally, simulation results are shown to demonstrate the effectiveness of the proposed control strategy.
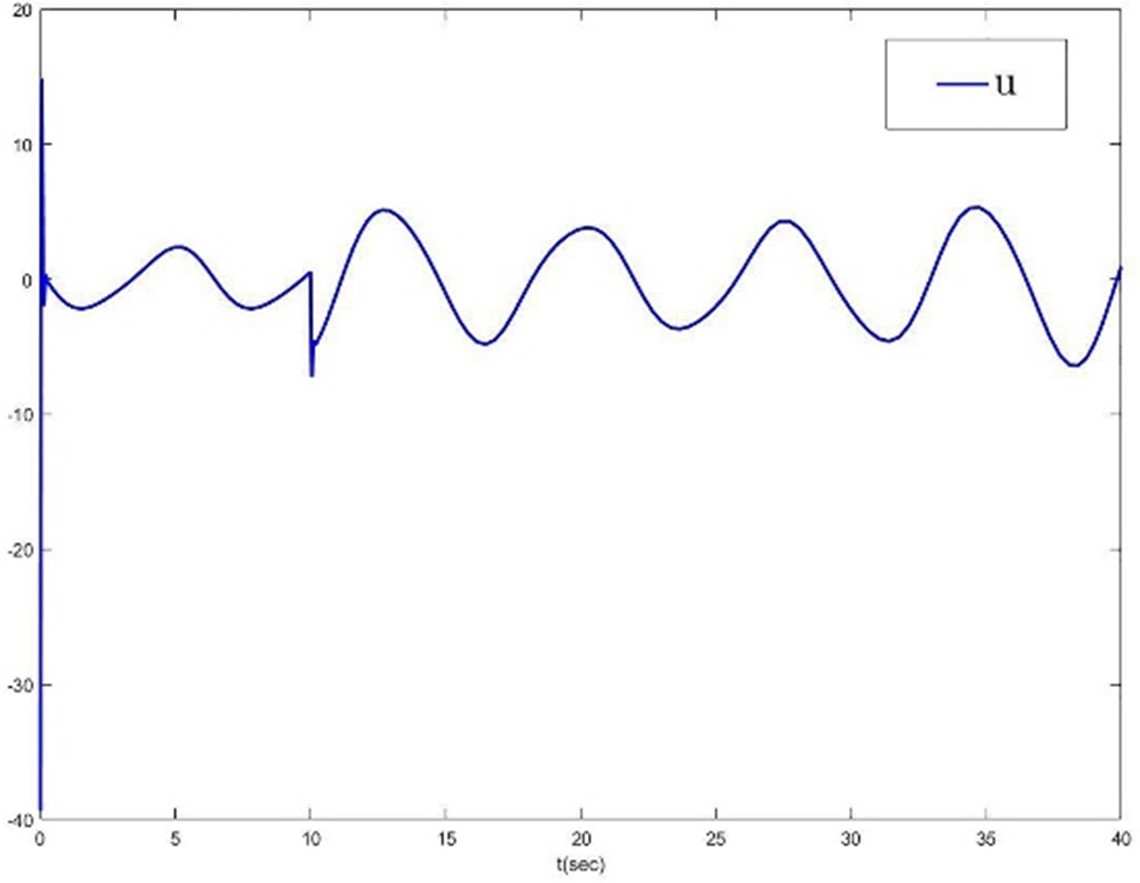
The trajectory of u.

Optimal control analysis of coffee berry borer infestation in the presence of farmer's awareness
农民意识下咖啡果螟虫害的优化控制分析
作者:Mohammedsultan Abaraya Abawari et al.
摘要:
Coffee is the most critical stimulant beverage in the world and represents a significant source of income in many tropical and subtropical countries. In this paper, a deterministic mathematical model has been formulated to describe the infestation dynamic of coffee berry borer (CBB) using a system of non-linear ordinary differential equations with farmers' awareness and optimal control. The system has two equilibrium points, namely the CBB free equilibrium point and the endemic equilibrium point which exist conditionally. The basic reproduction number, which plays a vital role in mathematical epidemiology, was derived. The qualitative analysis of the model revealed the scenario for both CBB free equilibrium and endemic equilibrium points. The local stability of the equilibria is established via the Jacobian matrix and Routh–Hurwitz criteria, while the global stability of the equilibria is proven by using an appropriate Lyapunov function. The normalized sensitivity analysis has also been performed to observe the impact of different parameters on the basic reproduction number. We extended the proposed model into an optimal control problem by incorporating two control variables, the effort made to reduce the colonizing females based on chemicals, traps, and biological control using entomopathogenic fungi such as Beauveria bassiana, that are applied to the surface of the coffee berries and kill the colonizing females of CBB when they drill an entry hole into the coffee berry and the effort made to increase the awareness of farmers through media campaign and education for the coffee farmer. Then the optimal control strategy is found by minimizing the number of CBB individuals considering the cost of implementation. The existence of optimal controls is examined using Pontryagin's minimum principle. Finally, the numerical simulations show agreement with the analytical results.
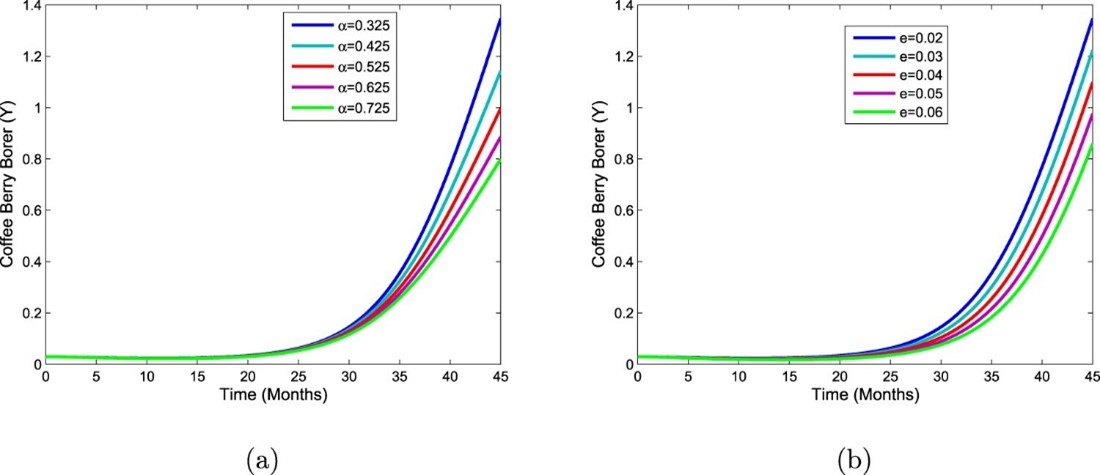
Impact of aware farmer growth rate and awareness rate on the CBB population.
审稿周期
从提交稿件到获取初审意见,平均需要6天
获取首个同行评审决定,平均需要40天
稿件一旦接受后,在线出版平均需要17天
为帮助更多科研人员选择更加合适的期刊,Taylor & Francis推出专栏——刊·见,该专栏致力于为读者和广大科研人员带来Taylor & Francis旗下期刊的详细解读,从期刊的基本情况、编委阵容、社会影响力到审稿速度、高被引文章等实用信息,专栏将为您带来最详细的介绍,让您更加全面地了解Taylor & Francis旗下优秀的国际期刊,帮助更多中国卓越科研成果顺利在国际期刊上发表。
https://blog.sciencenet.cn/blog-3574014-1420498.html
上一篇:【吉林大学邹晓龙副教授专访】突发公共卫生事件对金砖国家气候政策的影响
下一篇:刊·见 | 与Wood Material Science and Engineering一起探索木材科学的前沿技术