本文创新点

(1) 本文提出了一种核方法中无需增加模板尺寸的高效四阶权重，该方法在一维中仅使用三个等距点，即可达到四阶收敛速度。

(2) 证明了两个收敛结果，并对所提方法的有效性、收敛性、精度进行了数值实验验证。

(3) 给出了该方法在时间分数阶Black-Scholes偏微分方程上的应用，与现有方法相比，该方法在计算效率、计算精度、稳定性方面有明显优势。

研究背景及目的

径向基函数 (radial basis functions, RBFs) 在插值、偏微分方程等领域的应用中展现出诸多优点。在处理插值问题时，RBFs基于一组输入-输出数据对来近似一个函数。与其他插值方法相比，RBFs在高维空间中可以提供更精确的近似。近年来，RBFs在工程和科学领域引起了广泛关注。RBFs也可以用于函数近似问题，目标是找到一个函数来模拟给定系统的输入-输出关系。他们可以考虑被近似函数的全局和局部特征，从而进行更准确的预测。此外，RBFs可以模拟输入和输出变量之间的非线性关系，使其适用于线性模型不足的应用。这种灵活性源于RBFs中使用的非线性基函数的选择。

本文研究了如何在不增加模板尺寸的情况下提高计算效率，特别是近似收敛阶。事实上，在大多数已发表的文献中，在基于等距节点的一维中，当模板尺寸为三时，收敛阶不能大于二，这意味着提高收敛阶的唯一方法是增加模板尺寸，并考虑模板中四个或更多离散点。因此，为了提高收敛速度，在Hermite有限差分方法 (Hermite finite-difference, HFD) 下提出紧凑公式。为了计算这些紧凑公式 (特别是一阶和二阶导数) 的解析权重和局部截断误差，本文提出了径向基函数Hermite有限差分方法 (radial basis function-generated Hermite finite-difference, RBF-HFD) 的高效四阶权重。

模型及结果分析

本文首先阐述了RBF-HFD，进而给出一阶和二阶导数紧凑公式：

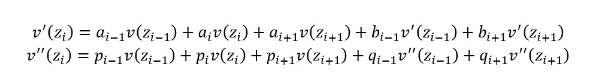
以及解析权重：

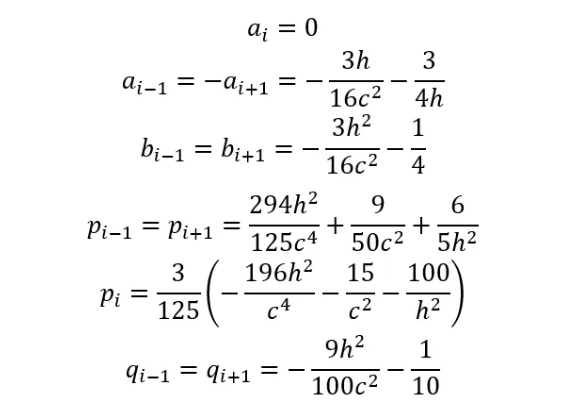
随后，给出了定理，证明紧凑公式四阶收敛。

在五个测试函数和时间分数阶Black-Scholes偏微分方程上验证，本文方法在计算效率、计算精度、稳定性方面明显优于诸如有限差分方法，径向基函数有限差分方法等现有方法。

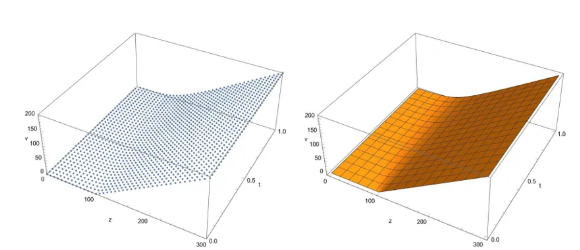
图1. 时间分数阶Black-Scholes偏微分方程数值结果。

图1展示了本文方法在时间分数阶Black-Scholes偏微分方程期权定价模型上的数值结果，左图为离散图像，右图为通过插值提取的连续图像。图1表明了本文方法的稳定性和正定性。

讨论与总结

本文提出了RBF-HFD的高效四阶权重，该方法使用多元二次RBFs的变体来近似函数的一阶和二阶导数。权重和局部截断误差的解析计算证明了该方法的计算效率。计算结果证实了该方法的有效性，表明了其在数值分析和求解偏微分方程问题中的各种应用潜力。未来的研究将侧重于使用RBF-HFD方法提高具有五个节点的模板上的收敛阶，并将其与有限差分方法，径向基函数有限差分方法的收敛速度进行比较。此外，还将探索将该方法应用于先进的无参数多重调和样条RBFs。

作者介绍

柳陶 

东北大学 (秦皇岛分校) 数学与统计学院

副教授，理学博士，新加坡南洋理工大学博士后。

研究方向：人工智能、应用数学、地球物理学、金融学的交叉学科研究，包括深度学习 (CNN、GAN、PINN)、强化学习 (AlphaGo)、多尺度方法 (多重网格、小波)、同伦方法、反问题。

Stanford Shateyi 

南非文达大学数学与自然科学学院数学与应用数学系

教授，理学博士，系主任。

研究方向：流体力学、数值方法、微分方程。

原文来自 Mathematics 期刊：https://www.mdpi.com/journal/mathematics

阅读英文原文：https://www.mdpi.com/2227-7390/12/7/1121

Mathematics 期刊介绍

主编：

Francisco Chiclana, School of Computer Science and Informatics, De Montfort University, UK

期刊主题涵盖纯数学和应用数学所有领域，重点发表代数、几何和拓扑、函数插值、差分和微分方程、计算和应用数学、概率与统计、数学物理、动力系统、工程数学、数学和计算机科学、数学生物学、网络科学、金融数学、以及模糊集、系统和决策等相关领域的文章现已被SCIE (Web of Science)、Scopus等重要数据库收录，JCR category rank: 21/489 (Q1) 。

2023 Impact Factor：2.3

2023 CiteScore：4.0

Time to First Decision：17.1 Days

Acceptance to Publication：2.6 Days