自1843年英国数学家哈密尔顿发现四元数以来，四元数及四元数矩阵一直受到广泛关注。20世纪70年代以来，四元数和四元数矩阵得到了更广泛的研究，相关理论广泛应用于理论力学、光学、计算机图形学、飞行力学与航空航天技术、量子物理、信号处理等领域。来自上海大学理学院的王卿文老师团队在 Symmetry 期刊发表了文章，介绍了一类Sylvester型四元数矩阵方程组可解的充分必要条件，并给出方程组可解时的通解表达式。

研究过程及结果

文章首先介绍了四元数的基本知识，强调了四元数代数是实数域上的非交换除环。研究者们对四元数和四元数矩阵在很多领域进行了深入研究，这些研究不仅扩展了数学理论，也发现了四元数和四元数矩阵在多个领域的应用。接着，文章引入了Moore–Penrose逆的概念，解释了它在矩阵理论中的重要性，特别是在处理奇异矩阵和最小二乘问题时的作用。此外，作者还回顾了一系列与矩阵方程相关的基本概念和引理，为后续建立可解性条件奠定了理论基础。

作者在文中利用所涉及四元数矩阵的秩和Moore-Penrose逆，建立了Sylvester型四元数矩阵方程组：

(1)

可解的充分性和必要性条件。随后，作者说明当满足可解的条件时，方程组的一般解可以用一种简洁的方式表示出来。此外，通过一个数值示例，作者对这些主要结果进行了验证，以验证结果的准确性。

作为该方程组 (1) 的应用，作者在四元数矩阵方程组：

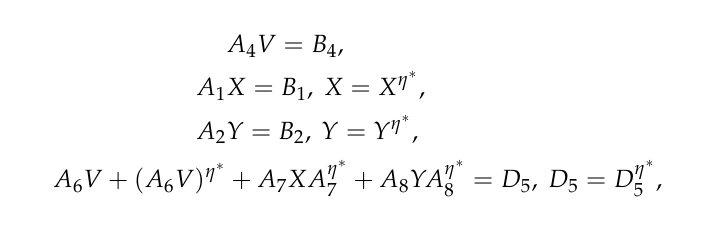
(2)

中考虑了一种特殊的对称解，即η-Hermitian解，并给出了方程组 (2) 具有η-Hermitian解的充分和必要条件，并在四元数方程组有η-Hermitian解时给出了一般解的具体表达式。

研究总结

作者通过使用Moore-Penrose逆和方程组 (1) 中系数四元数矩阵的秩，建立了方程组 (1) 的可解性条件，并在其可解时导出了其一般解的公式。并作为应用，导出了方程组 (2) 具有η-Hermitian解的必要和充分条件，以及一般解的表达式。作者还使用算法和数值算例验证了本文主要结果。本文对方程组 (1) 的研究结果不仅适用于实数和复数域，还适用于任何除环。此外，本文的主要结果也可推广到四元数代数系统上的张量方程。文章的整个研究过程凝练而深刻，对四元数矩阵方程组理论的推动和应用都具有积极的推动作用。

原文出自 Symmetry 期刊

Wang, R.-N.; Wang, Q.-W.; Liu, L.-S. Solving a System of Sylvester-like Quaternion Matrix Equations. Symmetry 2022, 14, 1056. https://www.mdpi.com/1641182

Symmetry 期刊介绍

主编：Sergei D. Odintsov, Institute of Space Sciences (IEEC-CSIC), Spain

期刊主题涵盖了所有科学研究中有关对称/非对称现象的理论和应用研究，主要包括数学、计算机、工程与材料、物理学、生命科学、化学等领域的最新进展。期刊已被 Scopus、SCIE (Web of Science)、CAPlus/SciFinder 等多家知名数据库收录。

2022 Impact Factor：2.7 

2022 CiteScore：4.9

Time to First Decision：16.2 Days

Acceptance to Publication：3.5 Days