43. 能否发展关于湍流动力学和颗粒物质运动行为的一般理论?
Can we develop a general theory of the dynamics of turbulent flows and the motion of granular materials？

《科学》杂志对这个问题的评述只有短短几句话，其最主要的意思是：统计力学在湍流和颗粒物质这两类非平衡体系上的失败展现了物理学中的一个尚未被完全填补的鸿沟，我们到底能不能为湍流和颗粒物质动力学建立一个统一的理论框架。所以，对于湍流和颗粒物质这两类复杂系统的演化，要想从复杂系统的角度来全新解读它们并非是一件容易的事情，下面就算抛砖引玉来科普和解读这个问题。

1. 多尺度的物质结构和运动规律

真实的自然界是一个多尺度的复杂系统，而复杂系统之所以复杂是因为其具有两个基本的特征：(1)高自由度；(2)非平衡。所以复杂系统就是一个处于非平衡态的多体系统。

人类所面对的世界之所以复杂，其中一个重要的原因就是这个世界形形色色的物质都是“由多尺度单元”所构成的多体系统。所谓的多尺度是指空间、时间以至于能量在数量级上的不同和表现。这种把复杂系统看成由独立单元构成的处理方法，经常被称为还原论。对于构成多体系统的独立单元，根据其尺度不同，描写单元的物理规律和方程也会截然不同。

图1 各种尺度单元构成的复杂系统图像

如果在宇宙的尺度下把宇宙看成一个单元，那么其运动规律满足爱因斯坦宇宙学方程；而在与人体尺度相当的宏观尺度下去研究物质单元的运动规律，其应满足万有引力的牛顿方程和经典麦克斯韦方程（此处不讨论生物个体自持单元组成的社会群体行为，可见科学问题(16)群体合作）；在更微观的尺度下，物质单元则遵从薛定谔方程的运动规律，而至于原子核以内的尺度则会出现更多不同的规律和方程（比如标准模型等），所以物质世界是多尺度的，而其运动规律也是多尺度的。当然如果我们可以将各种尺度的规律统一为一个方程，此即所谓的大统一理论，然而这个努力到现在还没有最终完成（可参考科学问题(5)大统一理论）。

所以根据人类目前的科学认知，我们依然要依靠多尺度的视角和理论来认识这个复杂客观世界的物质及其运动规律。而还原论认为，只要我们弄清楚某种尺度下多体系统独立单元的运动规律，那多体系统的规律就可以通过多体单元的集体动力学来认识清楚了。而这个还原论的解构思想在逻辑上不仅靠谱，而且在实践中也一直极为成功。

图2 还原论和整体论的哲学争论

在微观尺度下，物理学所研究的物质都可以看成是由大量原子构成的多体系统，而原子单元之间可以通过较强的相互作用（如化学健）结合为分子，分子则会通过更弱的比如范德瓦尔斯力自组织结合为高分子或团簇单元，而团簇再经过更弱的相互作用可以结合为颗粒体，最后由大量颗粒体或具有宏观尺寸的颗粒物质组成我们所面对的形形色色的宏观物质。

以上对物质结构的常规认识来源于物质都可以被分割为不同尺度的相对独立“单元”的事实，而这些单元可以是原子、分子、团簇甚至颗粒等等。例如在常温常压下有些物质在原子尺度就能构成宏观物质，也就是这种物质的原子之间的相互作用已经非常微弱，所以它可以看成由相对独立的原子单元构成的物质，比如惰性气体。而有些物质在分子尺度上单元间的相互作用才变得微弱，从而它可以直接被划分为相对独立的分子单元，如大多数气体（氢气、氧气、氮气等）以及大部分液体（如水、油等）等。当然有些物质则是由大量的原子或分子构成的相互作用非常弱的颗粒单元构成，也就是该物质可看成由大量的相互作用非常弱而相对独立的颗粒体构成，在这种单元视角下我们一般就称其为颗粒物质，例如沙堆、烟雾、云或更大的泥石流等等。

然而这种在不同尺度下选择不同单元去解构物质的方法决定于物质单元在哪个尺度上具有更好的独立性，所以构成多体系统单元的选择并非有明确的标准，而且这个单元的选择也并非一成不变，这显然是多体系统复杂性的另一个方面。选择不同的结构单元，会对复杂系统的描述产生本质的影响（如物理规律不同），尽管物质的整体性质和单元的选择无关，但单元的选择在复杂系统动力学的计算复杂度上有着本质的差别。系统选择不同尺度的单元，不仅意味着对其描述是否有效，而且还决定描述单元的物理规律是否相同。对大量由不同尺度单元（原子、分子、团簇、颗粒等）所构成的多体系统，描写其动力学行为的理论会根据单元尺度选择不同的动力学规律，在不同单元动力学的基础上多体系统的整体行为才由单元间的多体相互作用来决定。所以对多体复杂系统动力学行为的研究，目前有效的方法都是在适当单元解构的基础上采用适当的理论来处理。

2.多体复杂系统的连续介质理论

对多体系统主要有两种处理方法，一种是连续介质下的微分方程方法。该方法最具代表性的研究对象就是流体，发展出所谓的流体动力学理论。该方法认为流体由微元构成，这个微元宏观上可以是无限小，而微观上则必须无限大，所以每一个流体微元都满足牛顿方程。所以该理论是建立在无限可微时空的基础上的连续介质理论，其最主要的数学工具就是时间和空间的偏微分方程。

图3 流体动力学的速度场

人类对流体系统的研究历史非常久远，早在古希腊时期阿基米德就发现了流体静力学的阿基米德定律，17世纪帕斯卡研究了静止流体中的压力问题。流体运动学理论开始于欧拉，他将流体静力学中的压力概念推广到运动流体中，利用流体微元的牛顿方程建立了描写无粘滞流体的微分方程组：欧拉方程；之后伯努利利用流体微元的机械能守恒推导出无粘滞内耗的不可压缩流体的伯努利方程；最后就是将二者结合起来并推广到粘性流体的纳维-斯托克斯方程，该方程是流体力学中一个至今不清楚其解结构的方程，125个科学问题中在最后会专门介绍这个方程，故事很精彩，咱们到时介绍，此处从略。

而这里要提到它是因为在流体力学中有一种奇特的流体动力学现象：湍流（如图4所示），而著名的纳维-斯托克斯方程的解中有一类解和这个湍流非常相似，即利用该方程的数值模拟可以展现和湍流现象完全相似的流体图像。然而至于是否可以用纳维-斯托克斯方程的解去最终理解湍流现象，目前并非完全达成共识，这是因为湍流现象显然是一种典型的非平衡过程，而纳维-斯托克斯方程的解给出的是一个处处可微的速度流场解，其本质上是一个局域的平衡解，似乎无法出现这么多湍流漩涡中心那样的速度为零的流场奇点（见图5）。

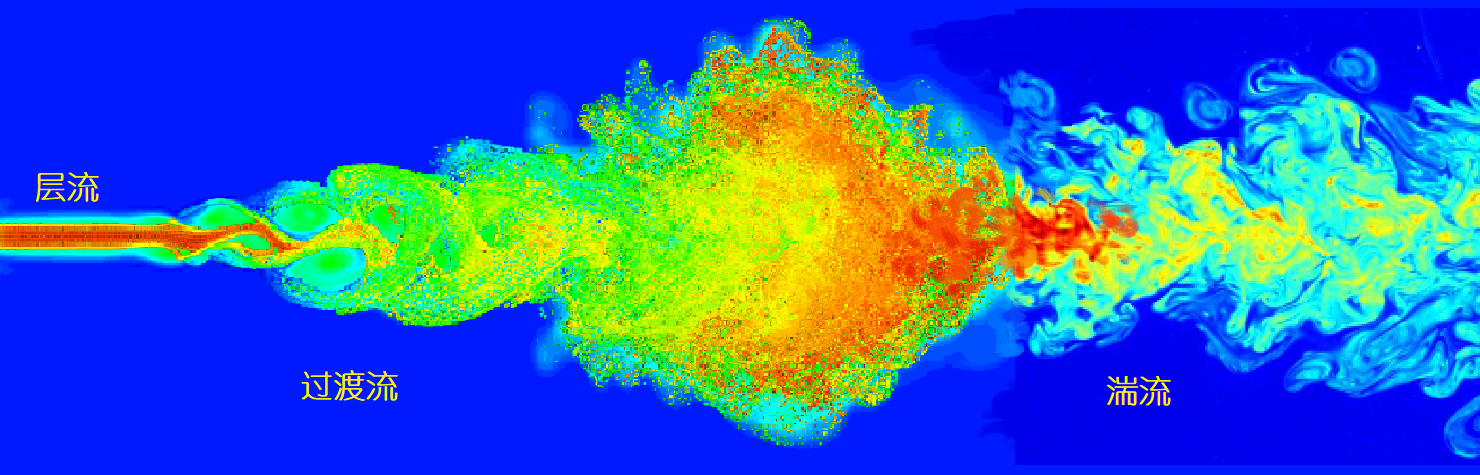
图4 湍流的多尺度涡旋

那到底什么是湍流？一般的维基百科会这样介绍：湍流是流体的一种流动状态。当流体流速很慢时，流体分层流动互不混合，称为层流或片流；流速增加，层流间开始出现波浪状摆动，摆动频率及振幅随流速的增加而增加，称为过渡流；当流速增加到一定程度时，层流被流场中的许多小漩涡所破坏和混合，此时流体作不规则运动，这种运动就称为湍流，又称为乱流、扰流或紊流。

图5 湍流中的相干结构和速度为零的奇点

湍流的基本特征是流体中会出现各种尺度随机运动的涡旋。为了研究湍流中的这种复杂的涡旋演化过程，最早雷诺（Reynolds）利用纳维-斯托克斯方程导出湍流平均流场的基本方程：雷诺方程；然后引入统计、群论或拓扑的方法，对湍流的对称性和几何不变性进行了理论分析；20世纪70年代提出拟序结构概念研究了湍流的相干性结构等等。显然湍流是复杂流体系统的一个非平衡态的流体演化过程，这个过程由于缺少统计基础而无法将统计力学的理论方法有效应用于湍流现象，所以目前湍流依然是一个不断向前发展的研究方向。

3.多体系统的集体动力学理论

对多体系统的另一种理论方法就是通常的概率统计方法，具体根据构成多体系统的单元尺度来选择不同的统计理论。如果构成多体系统的单元是原子或分子尺度（纳米尺度），则主要采用量子的微观统计方法，即采用量子多体理论的薛定谔方程来进行研究，称为多体系统的微观统计理论。然而建立于量子理论之上的量子多体问题的困难在于构成系统的单元数量巨大（自由度巨大），实际上无法直接求解多体系统的薛定谔方程（计算复杂度很高）。为了有效研究多体系统，通常采用宏观统计的理论方法。宏观统计方法需要根据不同系统采用两种方式来降低多体系统的单元自由度：（1）依然采用微观单元如原子分子（自由度保持），但整体利用宏观概率统计的方法进行研究，其代表就是热力学与统计物理。（2）采用宏观尺度的单元如颗粒体或介质微元（粗粒化降低了自由度），采用牛顿方程对单元进行描述，而系统整体通过耦合牛顿方程进行宏观动力学的研究。这个方法的代表如分子动力学、网络耦合动力学以及群体动力学方法等等。

图6 沙堆的集体动力学

这两种方法的概率统计主要是建立于宏观平衡态基础上的热力学与统计物理理论。统计理论之所以能处理高自由度的多体系统，是因为它是建立于宏观量基础上的概率理论，本质上是对平衡态系统或系综的统计，如果研究空间或时间上的动力学细节，那这个方法则是无能为力的。而另外一个采用宏观的网络单元或颗粒单元，单元整体采用宏观量的动力学方程或牛顿方程来描写，整体则采用所谓集体动力学的方法研究复杂系统的演化过程。正是在这种方法的基础上，人们开始认识到集体动力学中所谓的非平衡过程及其所谓的协同、同步和涌现的思想，并继而发现了还原论的缺陷，也就是研究清楚物质单元的行为并不能得到系统的整体行为，系统整体会出现单个单元所不具有的特征，用安德森的一句名言概括就是：多者异也（More is different） 。

在利用耦合牛顿方程研究群体动力学的方法中同样存在一个非常典型的系统，就是所谓的颗粒物质系统。当然由怎样的颗粒单元组成的系统才是颗粒物质研究的范畴，严格来说没有明确的界限，但目前颗粒物质的基本概念认为构成系统的颗粒单元大小或尺寸一般要大于1微米，如果颗粒单元小于1微米，那其和连续介质的流体系统或量子多体系统就没有什么本质的差别了。

图7 颗粒物质的堆积

那到底颗粒物质在研究什么？颗粒物质最典型的研究对象就是沙丘，利用颗粒物质理论可以研究沙丘的演化。生活中经常见到的颗粒物质比如烟尘、粉末、药片、粮食、沙石等等，这些颗粒物质在集体运动时所形成的颗粒流具有和连续介质如流体不同的动力学行为，比如烟尘的湍流，粉末的流动、沙尘暴、雪崩现象、山体滑坡、泥石流、地震固体结构的垮塌等等现象，都和颗粒物质的动力学行为有关。当然颗粒物质的初始问题是其堆积的静力学问题，如著名的沙堆模型、粮仓粮食的堆积、或硬币以及不同积木的堆积问题。当然沙堆模型主要是用来研究自组织临界现象的，但其对理解颗粒物体稳定堆积有非常好的启发作用。这个方面最著名的工作是1895年贾森(Janssen)所提出的颗粒体单层堆积高度的计算公式：Janssen公式。

颗粒物质动力学的特点是多尺度多规律，由于颗粒物质粒子间的非弹性、非对心碰撞，颗粒物质在不同条件下能表现出气体、液体、固体多种动力学属性。颗粒物质的研究非常复杂，不仅在于颗粒物质的粒子之间的碰撞摩擦，它和其他介质的混合，比如空气或连续介质的混合，其动力学行为有时等同于气体，有时会“板结”为不同形状的固体，有时又犹如均匀流动的液体，这些行为会随着颗粒物质内部粒子的尺寸、密度、摩擦力、压力、运动速度以及与其他介质的混合比、边界条件、初始条件等而发生复杂的动力学变化，目前还没有一个完整的理论框架去描述。其所表现的有趣现象比如颗粒物质的不同尺度单元分层的巴西果效应（据说巴西人在巴西果的运输中发现小尺寸的果子都会集中在车厢的底部，也就是不同尺度的颗粒物质在振动摇晃或扰动中会发生分层现象，大尺度的颗粒会分布在上部，小尺度的颗粒会沉到下部）。这个现象在生活中也会经常见到，比如我们用簸箕或筛子去筛选不同大小和轻重的东西。另外在振动平台上的沙子会形成自组织的花纹或发生奇特的怪波激发跳动现象，比如法拉第发现颗粒体在振动容器中的特殊对流现象，雷诺发现颗粒物质加压的膨胀现象，这些都是颗粒物质集体动力学的特殊表现。

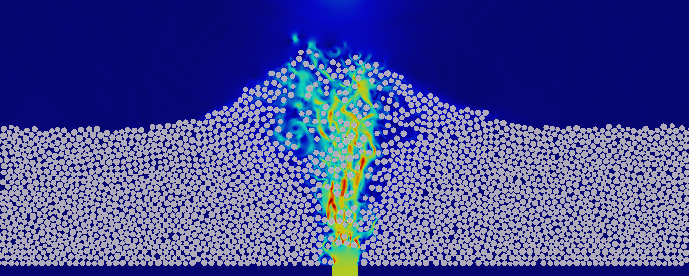
 图8 颗粒物质的特殊动力学现象

4.湍流和颗粒物质的统一理论框架

根据以上对湍流和颗粒物质的介绍，我们会发现这两类系统都能够表现出多尺度行为的非平衡复杂系统特征。湍流中的涡旋和颗粒物质中的从流体、到液体到固体的多尺度颗粒行为变化，都能表现出二者相似的多尺度特征。其次，湍流之中的自由度变化，即从低自由度的层流向多自由度的周期涡流再到多尺度自相似的相干涡旋结构，本身就是流体从低自由度向高自由度的分化过程；而颗粒物质受力后可以从固体，向表面流体，最后到整体流动的液体运动，其行为也存在自由度的分化增长现象。所以二者相似的动力学行为似乎在暗示我们：可以在一个更基本的理论视角下用一个统一的理论框架去描述二者的动力学行为，然而这个问题现在并没有肯定的答案。