一，模糊理论在人工智能发展蓝图中的位置

在1950年代计算机刚起步时期，关于计算机应该如何构造有两种理论：一种理论是冯·诺依曼的“CPU+存储器”结构，另一种理论认为计算机应该模拟人脑的结构与功能。冯·诺依曼在1958年出版的名著《计算机与人脑》中，将计算机和人脑放在一起来讨论和比较。

在后来计算机学科的发展中，冯·诺依曼的“CPU+存储器”结构取得了巨大的成功，造就了现代计算机学科与产业，深刻地改变了人类的生活方式，而模拟人脑的研究方向（人工智能）却步履艰难，直到最近几年才有一点后来居上的势头。那么，在计算机和人工智能的发展蓝图中，模糊理论是一个什么角色呢？见下图：

就模拟人脑而言，神经网络试图模拟人脑的硬件结构（大量神经元网络化链接），而模糊系统则试图模拟人脑的“软件结构”（fuzzy-rule-based reasoning，基于模糊规则的推理）。心理学研究表明，人脑的工作方式分为两个系统：一个快系统，一个慢系统，见Kahneman的心理学名著“Thinking，Fast and Slow”：

快系统主要完成那些不需要思考就能马上做出反应的事情，比如图像识别、语音识别等；慢系统完成那些需要进行思考、比较复杂的事情，比如逻辑推理、类比、联想等。现在的深度神经网络能够很好的完成人脑快系统的工作，比如图像语音文字识别等，而不能有效完成人脑慢系统的工作。模糊系统正是为完成人脑慢系统的功能而设计的。

模糊系统是由模糊规则通过模糊逻辑近似推理构建而成的，是最接近于人脑逻辑思维方式的数学模型。人脑需要在复杂和充满不确定性的环境下进行逻辑思维，传统的0/1逻辑过于简单粗暴，不能有效的描述人脑复杂的逻辑推理过程。模糊逻辑，正如Zadeh所说，并不是模糊的逻辑，而是关于不精确变量的近似推理逻辑。模糊逻辑是一门严谨的数学学科，有着丰富的内涵，为描述人脑在复杂和不确定环境下进行逻辑推理提供了众多的数学模型。数据时代的模糊理论又为模糊系统提供了学习功能，使其更加接近于人脑的思考与学习过程。

与神经网络的“黑箱操作”相比，模糊模型的一大优势是其可解释性，属于“可解释性人工智能”的范畴。神经网络是黑箱模型，一旦出错很难进行修正。比如，基于神经网络模型的自动驾驶系统，一旦出了交通事故，很难找出到底是神经网络的那些部分出了问题，因此很难对神经网络模型进行修正，也就无法保证不犯同样的错误，这严重阻碍了神经网络自动驾驶系统的推广应用。模糊模型可以解决这个问题：由于模糊系统由模糊规则一环套一环构建而成，如果系统出了问题，可以追溯到是那些规则出了问题，进而对这些规则进行修正与改进，确保系统不再犯同样的错误。

因此，我们将当下流行的基于深度神经网络的人工智能称作“初级人工智能”，而将基于深度模糊模型的人工智能称作“高级人工智能”：

初级人工智能：实现人脑快系统的各种功能，比如图像辨识、语音识别、文字转换等不需要思考、马上就能做出即时反应的人脑功能；

高级人工智能：实现人脑慢系统的各种功能，比如逻辑推理、类比思维、联想推广等需要思考、不能马上做出即时反应的人脑功能。

初级人工智能是现实，高级人工智能是下一步奋斗目标。为实现高级人工智能，模糊理论需要向深度模糊模型以及大规模网络化模糊模型的方向发展。

二、深度模糊系统

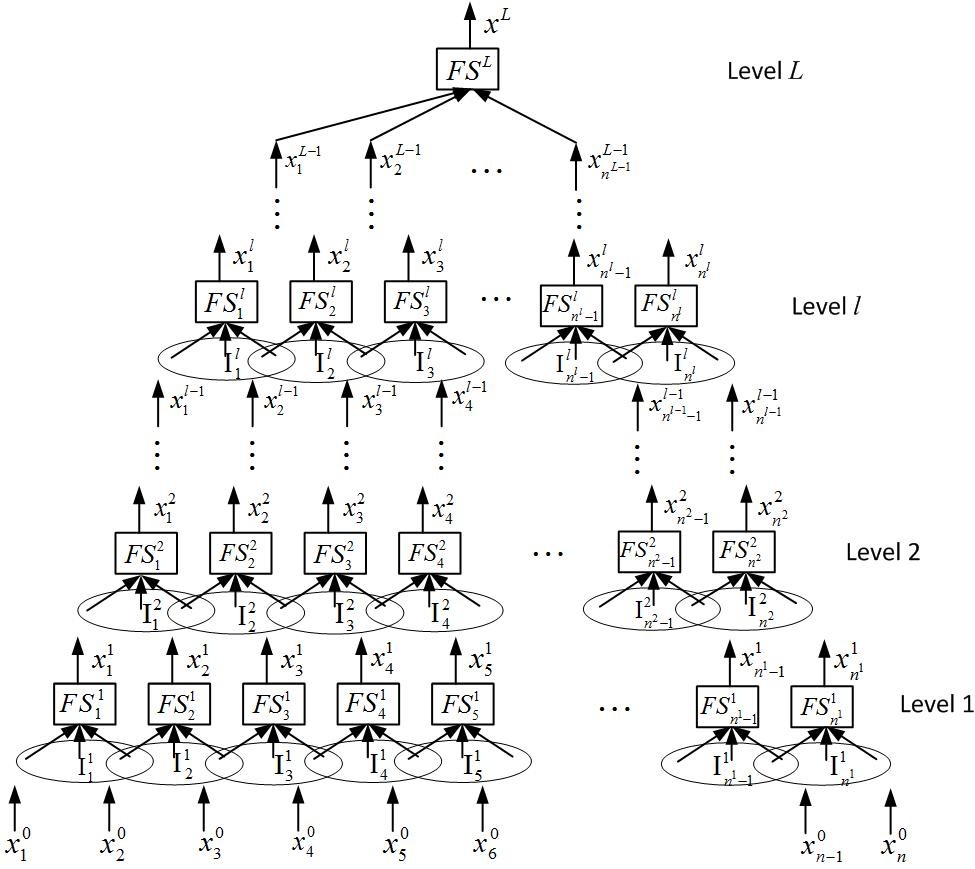
深度模糊系统也称作多层模糊系统，其概念很简单，就是将低维的简单模糊系统一层一层组合连接起来，形成适用于高维复杂问题的模糊系统模型，如下图所示，其中FS为低维度简单模糊系统：

（深度模糊系统）

多层模糊系统由Raju于1991年提出，至今已有三十多年了：

Raju, G.V.S., J. Zhou and R. A. Kisner, "Hierarchical fuzzy control", Int. J. Contr., vol. 54, no. 5, pp. 1201-1216, 1991.

同一时期，LeCun提出了当前人工智能最热门的卷积神经网络：

LeCun, Y. et al., “Handwritten digit recognition with a back- propagation network”, Proc. Advances in Neural Information Processing Systems: 396–404, 1990.

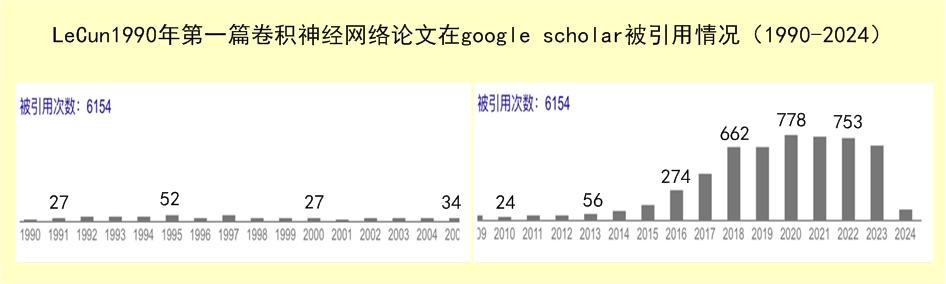
多层模糊系统与卷积神经网络有着相似的地方，两者都是把简单的低维系统一层一层组合连接起来用于解决高维复杂问题。两者的不同在于，卷积神经网络以神经元作为基本的构建单元，而多层模糊系统的基本构建单元是低维模糊系统。Raju的这篇多层模糊系统开创性论文至今（2024年2月）在google scholar 只有554次引用，而LeCun的这篇卷积神经网络开创性论文被引用6154次，两者相差巨大。但是，LeCun这篇论文的引用主要集中在2013年之后，在论文发表的前二十年被引用是非常少的（1990-2010二十年总共只有642次引用），见下图：

多层模糊系统于1991年提出之后，最初几年并没有进一步深入的研究。直到1997年左右，我在完成了模糊系统与模糊控制的标准教材“A Course in Fuzzy Systems and Control”之后，我觉得当时模糊理论的一个主要不足是难以解决高维问题，模糊系统下一步应该向多层次模型的方向发展，使其能够适用于解决高维复杂问题。于是，我从多层模糊系统最基本的逼近性能和学习算法入手，于1998和1999年发表了下面两篇论文，分别证明了多层模糊系统也具有万能逼近性能，以及提出了用BP算法训练多层模糊系统的具体方法：

L. X. Wang, “Universal approximation by hierarchical fuzzy systems,” Fuzzy Sets and Systems, Vol. 93, pp. 223-230, 1998. 

 L. X. Wang, “Analysis and design of hierarchical fuzzy systems,” IEEE Trans. on Fuzzy Systems, Vol. 7, No. 5, pp. 617-624, 1999.

这两篇论文二十多年来在google scholar只有644次引用，具体分布见下图：

  比较上面多层模糊系统论文的被引用分布图和LeCun的卷积神经网络论文的被引用分布图，可以发现两者在其发表后前二十年的情况差不多（LeCun的卷积神经网络开创性论文在发表后二十年合计被引用642次），都是小众研究领域。卷积神经网络后来的飞跃式发展，一个主要原因是Hinton于2006年提出了一个快速学习算法，可以有效快速地训练深度神经网络:

Hinton, G. E., Osindero, S. & Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Comp. 18, 1527–1554 , 2006.

之后，在2012年，Hinton等人将这些先进的学习算法应用于卷积神经网络，在图像识别领域取得突破性进展：

Krizhevsky, A., Sutskever, I. & Hinton, G. ImageNet classification with deep convolutional neural networks. In Proc. Advances in Neural Information Processing Systems 25 1090–1098, 2012.

从而开启了当前的人工智能热潮（上面这篇论文的第二作者Sutskever就是OpenAI的联合创始人和首席科学家）。

1990年代末期发表了上面两篇多层模糊系统的基础性论文之后，我就离开了模糊领域，转去研究金融系统机理建模和算法交易。虽然后续有其他学者跟进研究，但基本上属于跟踪性研究，没有突破性进展。比如，多层模糊系统的两大问题就一直没有解决：一是随着系统层数和维数的增加，BP学习算法收敛速度太慢，所以需要开发新的快速学习算法来构建多层模糊系统；二是多层模糊系统层与层之间变量的物理意义不明确，因此失去了模糊系统可解释性这个最大的优点。到了2018年左右，看到深度神经网络的巨大成功，想想二十年前我们两个领域并驾齐驱，后来由于Hinton等人的持续努力，深度神经网络取得巨大成功，而我们做多层模糊系统研究的人却各奔东西。于是，我觉得我应该回过头来把二十年前的工作捡起来，继续推进多层模糊系统理论向前发展。具体的讲，就是需要开发一种新的快速学习算法来构建多层模糊系统，同时构建出的多层模糊系统层与层之间变量要有明确的物理意义，从而使得构建出的多层模糊系统具有清晰的可解释性。2020年，我完成了这项工作，发表了下面这篇论文：

L. X. Wang, “Fast training algorithms for deep convolutional fuzzy systems with application to stock index prediction,” IEEE Trans. on Fuzzy Systems, Vol. 28, No. 7, pp. 1301-1314, 2020.

下面简单介绍这个快速学习算法的基本思路，以及构建出的多层模糊系统如何具有清晰的可解释性。

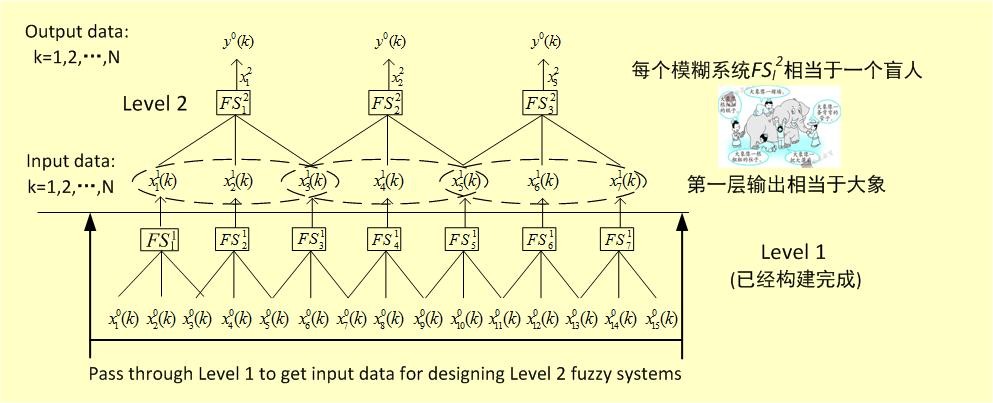
这个多层模糊系统快速学习算法基于两个基本思路：一是盲人摸象，二是一层一层盖高楼。具体地讲，首先构建多层模糊系统的第一层，然后在第一层的基础之上、用同样的方法构建第二层，之后在第二层之上构建第三层，以此类推，总层数可以自由选择。每一层的构建方式采用盲人摸象的思路，用多个低维模糊系统覆盖高维输入空间：每个低维模糊系统相当于一个盲人，高维输入空间相当于大象。具体算法如下：

多层模糊系统快速构建算法：

第一步：基于给定的高维数据集，用Wang-Mendel算法构建第一层的模糊系统，如下图：

第二步：将原始输入数据通过构建好的第一层形成新的数据集，基于新的数据集用Wang-Mendel算法构建第二层的模糊系统：

第三步：以此类推，构建第三层、第四层、…，直到最后一层。

这个多层模糊系统构建算法具有以下优点：

优点1、快速。由于数据在Wang-Mendel算法中只使用一次（一个数据点产生一条模糊规则，然后将这些模糊规则按区域合并），不需要BP算法的循环迭代，所以整个多层模糊系统构建的速度非常快。

优点2、可解释性强。由于每一层中的每一个低维模糊系统相当于一个盲人，所以多层模糊系统中每一层的作用可以理解为对低一层观察数据的归纳提炼。比如，如果原始观察对象是大象，那么经过第一层盲人们（第一层的低维模糊系统）的观察处理之后，大象变成了柱子（大象的腿）、棍子（大象的尾巴）、墙（大象的身子）、蒲扇（大象的耳朵）、管子（大象的鼻子）等，这些局部的观察变量构成了第二层低维模糊系统的输入空间。接着，和第一层同样的操作，第二层的盲人们（低维模糊系统）再进一步将这些变量抽象总结，形成第三层模糊系统的输入空间，以此类推，直到最后一层。所以，多层模糊系统中间变量的物理意义就是这些局部观察的抽象总结，越到高层抽象总结的越全面准确，直到最后得出大象这个正确的结论。由于每一个低维模糊系统都是由简单的模糊规则构成，所以整个多层模糊系统就是简单模糊规则的并联（同一层）和串联（层与层之间）构成的一个“透明”的模型，具有明确的可解释性。

优点3、如果出错很容易改正。由于多层模糊系统的可解释性（简单模糊规则的并联和串联），如果系统在某个应用场景出错（比如由其控制的自动驾驶车辆发生交通事故），很容易找出在这个场景下激活的模糊规则，对这些模糊规则进行修改就可以避免同样的错误，见下图：

上图左边表示一个低维模糊系统，其输入空间由模糊规则覆盖。虽然这些模糊规则的边界是从重叠的，但一个点上有一个发挥主要作用的模糊规则，可以用其行动参数（模糊规则行动部分模糊集合的中心点）c^ij来表示。上图右边表示由这些低维模糊系统构建的多层模糊系统，当其输入点为出错场景时，可以找出是哪些模糊规则在出错场景发挥主要作用，对这些模糊规则进行修改，就可以保证系统在相同的情形下不再犯同样的错误。修改的方法，可以是用新的正确输入输出数据，用Wang-Mendel算法把这些出错的模糊规则重新设计一遍。

优点4、计算量小，适合于在简单设备（比如手机）上实现。现在的人工智能神经网络大模型计算量庞大，尤其是新数据的学习过程需要反复迭代，所以只能在云端实现，无法在用户端的简单设备（比如手机）上进行。比如ChatGPT、Sora等，用户只能将问题发到云端，由云端大模型给出答案发还给用户，用户自己不能对模型进行修改，也无法通过自己的数据建立自己的模型。设想一下，如果有这样一个模型，大家都可以下载到手机上，然后每个人都可以用自己的图像、语言等数据来训练这个模型，使其不断改进更新，形成自己独特的模型来完成各种现在只能在云端大模型才能完成的工作，比如文本生成、视频生成等。多层模糊系统的构建算法简单快速，模型透明紧凑，可以在用户端的简单设备上实现，使得每个人都能拥有由自己训练出来的、属于自己的人工智能模型。

三、模糊舆情网络（社会心理学理论的数学模型）

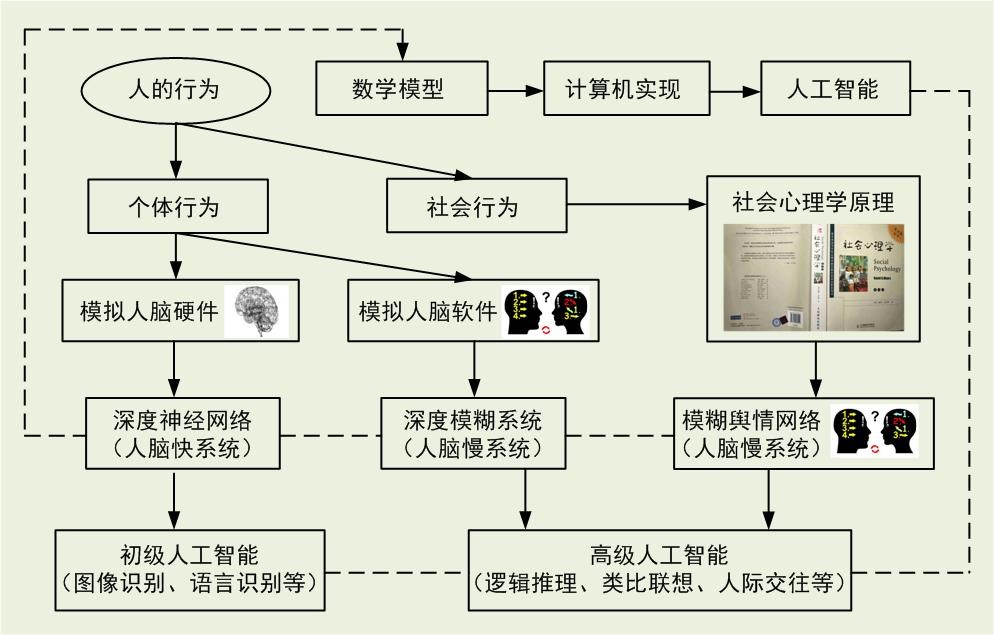
人工智能的核心是建立人脑以及人的各种行为的数学模型，然后通过计算机来实现这些数学模型及其相应的算法，进而形成具有人类智力功能的机器（人工智能）。人的行为可以大体分为个人行为和社会行为，所以建立人的个人行为和社会行为的数学模型是人工智能发展的重要基础性环节，见下图：

人的个体行为可以通过模拟人脑硬件（深度神经网络）或者模拟人脑软件（深度模糊系统）来建立数学模型，如本文前两节所介绍。人的社会行为是社会心理学的研究范畴：

社会心理学提出了众多关于人的社会行为的基本理论，比如：actor-observer difference theory（行动-观察者区别理论）, altruism theory（利他理论）, arbitration theory（仲裁理论）, attribution theory（归因理论）, bargaining theories（讨价还价理论）, belief perseverance theory（信念韧性理论）, bystander effect theory（旁观者效应理论）, cognitive dissonance theory, cohesiveness theory（凝聚力理论）, collectivism theory（集体主义理论）, compliance theories（服从理论）, correspondence bias theory（交流偏差理论）, fearful attachment theory（恐惧依附理论）, frustration-aggression theory（挫折攻击理论）, illusion of control theory（虚幻控制理论）, illusory correlation theory（相关幻觉理论）, mirror-image theory（镜像理论）, need to belong theory（归属感理论）, normative influence theory（规范影响理论）, overconfidence theories（过度自信理论）, representativeness theory（代表性理论）, rosy retrospection theory（玫瑰回顾理论）, self-affirmation theory（自我肯定理论）, self-fulfilling prophecy（自我实现理论）, sleeper effect theory（睡眠者效应理论）, social comparison theory（社会比较理论）, social-exchange theory（社会交换理论）, social loafing theory（躺平理论）, social trap theories（社会陷阱理论）, stereotype theories（榜样理论）, terror management theory（恐惧管理理论）,…，等等。

人工智能理论的一项重要任务，就是建立这些社会心理学理论的数学模型，进而用计算机实现这些数学模型及其相应的算法，让机器具有人的社会行为特征。这是迈向高级人工智能非常重要的一步。下面介绍的“模糊舆情网络”就是这样的一套全新的理论，为描述社会心理学理论与现象提供了一套基础的数学框架和数学模型。

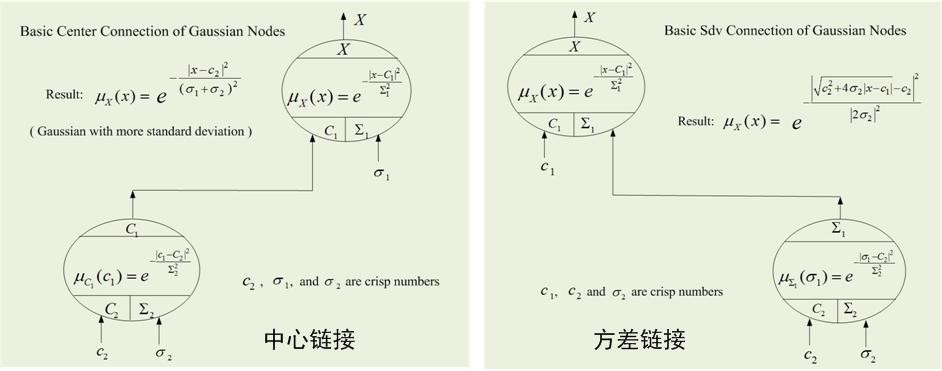
模糊舆情网络（Fuzzy Opinion Networks）最基本构建单元（类似于神经网络的神经元）是一个高斯模糊集合，称作“模糊节点（fuzzy node）”，其中高斯隶属函数的中心点表示“观点（opinion）”、方差项表示“观点的不确定性”。比如，中心点是一位评委给一项科研成果的打分，而方差项表示这位评委在这个科研领域的专业程度：如果评委是这个领域的一线专家，则方差项较小（表示打分可信度高）；如果评委是外行，则方差项较大（表示打分可信度低）。一个模糊节点有两个输入（观点和观点的不确定性）和一个输出（模糊集合本身），模糊舆情网络就是模糊节点的各种链接组合（类似于神经网络是神经元的各种链接组合），如下图所示：

模糊节点的链接方式分为两种：静态链接和动态链接，其中静态链接是基础，动态链接是在静态链接的基础上加入反馈而形成的。静态链接最基本的形式是中心链接和方差链接，如下图所示：

中心链接保持观点（opinion）不变，但观点的不确定性是两个节点不确定性的叠加。方差链接比较复杂，观点和观点的不确定性都发生变化。比如，当我们对一位评委的专业水平产生质疑时，最终的评分和评分的不确定性都会发生变化。模糊舆情网络理论为这些变化提供了具体的数学模型。

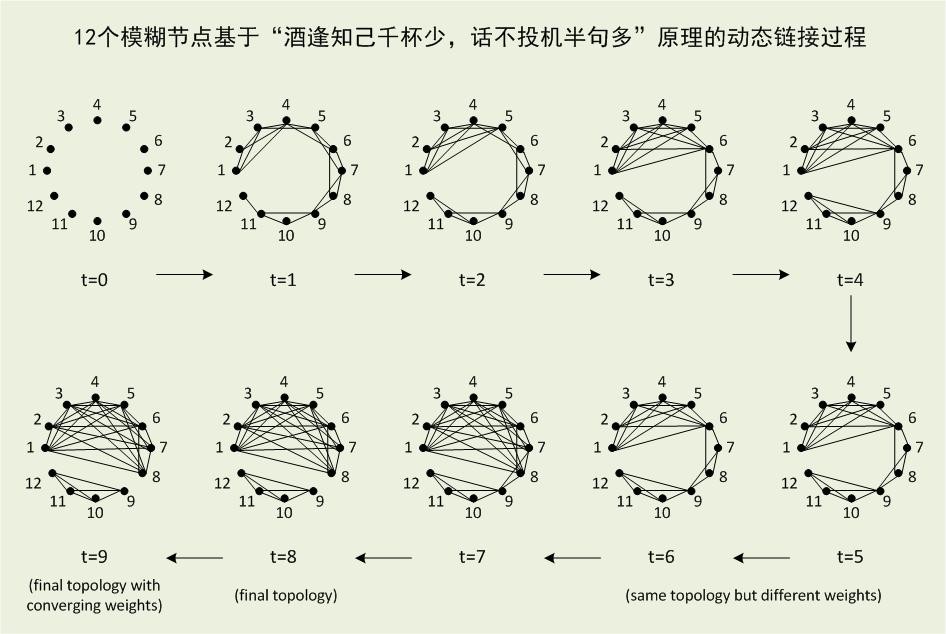
模糊节点的动态链接为描述各种社会心理学现象提供了丰富的数学模型。比如，基于“酒逢知己千杯少，话不投机半句多”这样的基本社会心理学现象，可以构造出相应的动态模糊舆情网络模型，来动态地刻画社交网络的形成过程，如下图所示：

模糊舆情网络理论的第一篇开创性论文是：

L. X. Wang and J. M. Mendel, “Fuzzy opinion networks: A mathematical framework for the evolution of opinions and their uncertainties across social networks,” IEEE Trans. on Fuzzy Systems, Vol. 24, No. 4, pp. 880-905, 2016.

这篇论文是我博士毕业二十四年之后再一次和导师合作的论文，也是至今唯一的一次合作。模糊舆情网络被成功地应用于投资者社交网络，得到投资者社会心理驱动的价格动态方程：

L. X. Wang, “Modeling stock price dynamics with fuzzy opinion networks,” IEEE Trans. on Fuzzy Systems, Vol. 25, No. 2, pp. 277-301, 2017.

另外，多层模糊舆情网络为人类社会最常见的等级化架构建立数学模型，可以定量分析信息自上而下和自下而上的传播以及融合过程，将这些重要社会现象的研究从定性论述推向基于数学模型的定量分析：

L. X. Wang, “Hierarchical fuzzy opinion networks: Top-down for social organizations and bottom-up for election,” IEEE Trans. on Fuzzy Systems, Vol. 28, No. 7, pp. 1265-1275, 2020.

  路遥遥兮修远兮，吾将上下而求索。深度模糊系统和模糊舆情网络开启了模糊理论迈向新时代的大门，随着这些刻画人类高级智能的数学模型和算法在分布式并行计算设备上的实现，模糊理论必将引领人工智能下一波浪潮，让具有高级智能的类人机器人走进千家万户，成就模糊理论最辉煌的计算时代（2015-2040）。

四、2040年的模糊理论长啥样？

父亲：咱家现在也就是一只小鸡

儿子：小鸡以后呢？

父亲：鸡养大了就变成了鹅

儿子：鹅以后呢？

父亲：鹅养大了就变成了羊

儿子：羊以后呢？

父亲：羊养大了就变成了牛

儿子：牛以后呢？

父亲：牛以后就是 … …

2040，咱们不见不散！