如果说数学是科学的语言，那么数据就是科学的食粮。到1990年初，虽然模糊理论取得了很好的应用，但其方法只是汇总专家经验，并不能利用数据对系统进行设计与优化。当时，模糊规则来自于专家问卷，由这些模糊规则构建的模糊控制就是经验控制，无法保证稳定性、最优性等基本性能要求。所以，作为一门工程学科，模糊理论要想取得突破，就一定要开辟新的理论与方法，充分有效地利用数据对模糊系统和模糊控制器进行设计、优化、在线调节等等。模糊神经网络与自适应模糊控制就是在这样的历史背景下产生的，它们的出现把模糊理论从“数学时代”推进到“数据时代”，迎来模糊理论三十多年的蓬勃发展。

一、模糊系统万能逼近定理

1980年代中期，神经网络领域迎来了第二次高潮（第一次高潮是1950年代计算机、控制论等学科的起步期，第三次高潮就是现在的人工智能热潮），其中一个主要原因是多层神经网络被证明具有万能逼近特性，因此适用于解决各种复杂问题。当时，由于模糊控制在日本欧洲等地的大量成功应用，模糊理论也迎来了发展的热潮。但是，当时的模糊系统由专家经验组合而成，是否具有广泛的适用性并没有坚实的理论支撑。因此，模糊系统是否和多层神经网络一样具有万能逼近特性，就成为模糊理论急待解决的基础性问题。

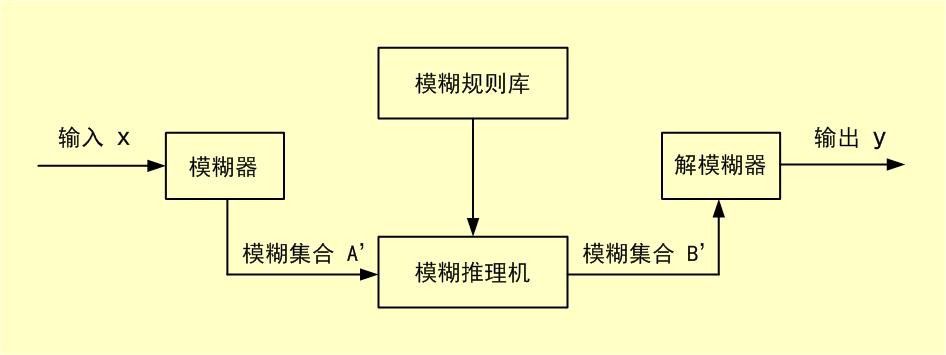
模糊系统由模糊规则库、模糊器、模糊推理机、解模糊器四个模块组成（当模糊系统作为控制器使用时，称作模糊控制器），见下图：

首先，输入变量x（高维向量）通过模糊器进行模糊化，变成输入空间上的模糊集合A’；接着，基于模糊规则库中的模糊规则，模糊推理机应用模糊逻辑原理对模糊集合A’进行推理运算，产生输出空间上的模糊集合B’；最后，解模糊器将模糊集合B’归结为系统的输出y。

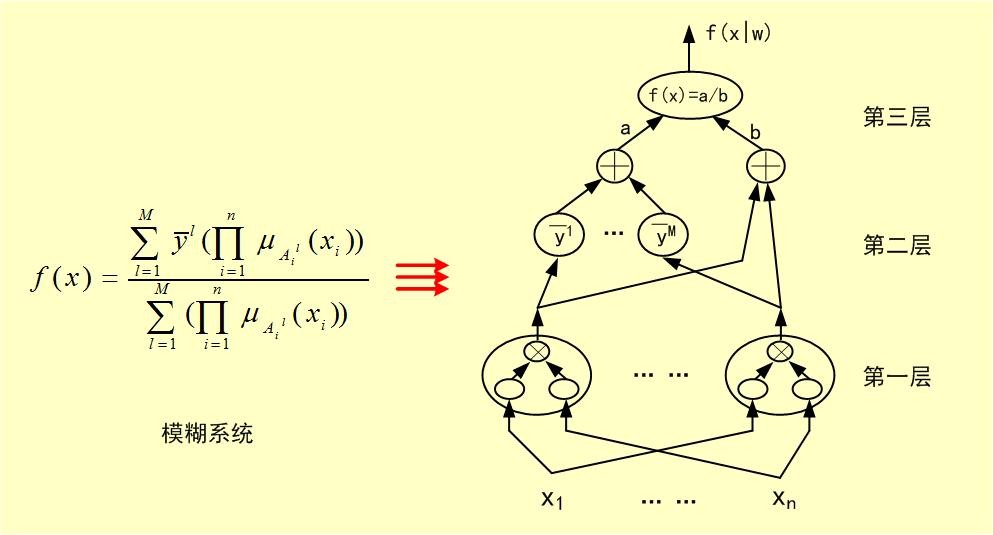
到1990年的时候，在模糊系统的具体实现中，上面四个模块是分别独立运行的，每个模块都有自己独立的一系列算法与运行模式。如果要证明模糊系统是万能逼近器，首先要做的是把模糊系统表示为从输入x到输出y的一个单一的数学函数y=f(x)，进而探讨f(x)是否具有万能逼近性能。这并不是一件直截了当的工作，因为每个模块都有其复杂的运算，比如模糊推理机中有高维空间的求优，解模糊器中有积分运算等。当时（1990年），我在美国南加州大学读博士第二年，修我们电机系Kosko教授的“神经网络与模糊系统”课程以及数学系的“高级泛函分析”研究生课程。经过仔细研究，我推导出了模糊系统从输入x到输出y的单一数学函数f(x)：

从模糊规则到数学函数：对于标准的模糊规则库（来自于专家经验的语言描述等），如果模糊器采用单值模糊器，模糊推理机采用乘积推理法则，解模糊器采用中心平均解模糊器，则这样的模糊系统可以表示为下图中的数学函数y=f(x)。

进而，利用高级泛函分析课程中学到的Stone-Weierstrass定理，我证明了模糊系统的万能逼近定理：

模糊系统万能逼近定理：对于任意非线性连续函数g(x)，总是存在上图中的模糊系统f(x)，在整个论域上可以任意逼近g(x)。

这个定理最先发表在1992年2月美国圣地亚哥召开的第一届IEEE模糊系统国际会议：

L. X. Wang, “Fuzzy systems are universal approximators,” Proc. 1992 IEEE International Conf. on Fuzzy Systems, pp. 1163-1170, 1992.

这是第一次在数学上严格证明了模糊系统具有万能逼近特性，因此与神经网络一样，适用于广泛的应用场景。这篇会议论文在google scholar被引用1644次。这项成果的完整期刊论文发表在IEEE神经网络汇刊：

L. X. Wang and J. M. Mendel, “Fuzzy basis functions, universal approximation, and orthogonal least squares learning,” IEEE Trans. on Neural Networks, Vol. 3, No. 5, pp. 807-814, 1992.

这篇论文在google scholar被引用3399次。模糊系统万能逼近定理为模糊系统在各行各业的广泛应用提供了坚实的理论支撑。

二、从数据产生模糊规则

如本文开始所说，到1990年初，模糊理论虽然在模糊控制领域取得成功的应用，但当时的模糊控制器只是专家经验的汇总，不能利用数据对系统进行设计与优化。如何利用数据来构建模糊系统，成为领域突破的关键。由于模糊系统是由模糊规则通过模糊逻辑构建起来的，利用数据构建模糊系统最简单、最直接的思路就是从数据产生模糊规则，然后利用这些模糊规则构建模糊系统。这就是我当时的想法。当时（1990年初，我去美国读博士的第一年第二学期），我正在修我们系（南加大电机系）Kosko教授的“神经网络与模糊系统”课程，需要做一个课程设计，于是我就提出了一个很简单的由数据产生模糊规则的方法：

第一步：用模糊集合交叉覆盖每个输入变量和输出变量（如下图中模糊集合A₁¹ A₁² A₁³A₁⁴ A₁⁵交叉覆盖输入变量x1，A₂¹ A₂² A₂³A₂⁴ A₂⁵交叉覆盖输入变量x2）。

第二步：对应于每一个数据点，得到每个输入输出变量在该数据点隶属度最大的模糊集合，用这些模糊集合构建模糊规则，一个数据产生一条模糊规则（如下图中三个数据点对应的隶属度最大模糊集合分别为A₁¹ A₂⁴，A₁² A₂²，A₁⁵ A₂¹，产生的模糊规则分别为IF x1 is A₁¹ and x2 is A₂⁴ ,THEN y is B1； IF x1 is A₁² and x2 is A₂² ，THEN y is B2； IF x1 is A₁⁵ and x2 is A₂¹ ,THEN y is B3）。

第三步：将重叠的模糊规则（IF-part相同的模糊规则）合并，形成模糊规则库，构建模糊系统。

（Wang-Mendel算法）

这个课程设计最后形成下面的论文：

L. X. Wang and J. M. Mendel, “Generating fuzzy rules by learning from examples,” IEEE Trans. on Systems, Man, and Cybern., Vol. 22, No. 6, pp. 1414-1427, 1992.

这篇论文在google scholar被引用4012次，是可解释性人工智能（从数据到知识）领域的经典。这个算法被称作Wang-Mendel算法，三十年来以其快速、高精度以及可解释性被广泛应用于众多领域，是行业标准、是后续算法性能比较的标杆。

三、模糊神经网络

基于数据设计生成模糊系统，除了上面的“数据—>模糊规则—>模糊系统”思路之外，另外一种方法就是利用数据直接“训练”模糊系统，使其匹配输入-输出数据对。这种思路与神经网络类似，因此称作“模糊神经网络”。第一篇利用这种思路来设计模糊系统的论文发表在1992年2月召开的第一届IEEE模糊系统国际会议：

L. X. Wang and J. M. Mendel, “Back-propagation fuzzy systems as nonlinear dynamic system identifiers,” Proc. 1992 IEEE International Conf. on Fuzzy Systems, pp. 1409-1418, 1992.

当时，为了证明模糊系统的万能逼近定理，我将模糊系统写成一个单一的数学函数y=f(x|w)（见本文第一节，其中w代表模糊系统的参数向量），因此很容易想到利用数据来调节模糊系统的参数，使得模糊系统匹配输入-输出数据对。即：给定输入-输出数据对（x^*(k),y^*(k)，k=1,2,3,…），确定模糊系统f(x|w)的参数向量w使得误差函数

J(k)=[y^*(k)-f(x^*(k)|w)]²

达到最小。最简单直接的方法是使用下面的梯度下降法来“训练”模糊系统的参数向量w：

w(t+1)=w(t)-a*(dJ(k)/dw)， t=0,1,2,3,…

使得误差函数J(k)收敛到最小。如果将模糊系统的参数向量“分层”来训练，就成为了神经网络最著名的“误差回传”（BP，Back-Propagation）算法。具体地讲，我将模糊系统f(x|w)表示成类似于神经网络的三层结构，然后利用上面的梯度下降算法来训练模糊系统的参数，见下图：

虽然我的这篇1992年会议论文是第一次利用神经网络的学习算法来训练模糊系统，但由于我并没有使用“模糊神经网络”这个说法，所以这篇论文并不是模糊神经网络领域的开端。这篇论文在google scholar只有712次引用。真正开创模糊神经网络领域的是Roger Jang的下面这篇论文：

J.S Roger Jang, “ANFIS: Adaptive-network-based fuzzy inference system,” IEEE Trans. on Systems, Man, and Cybern., Vol.23, No.3, pp.665-685，1993.

在这篇论文中，Roger Jang沿用模糊系统的传统结构，将“模糊器->模糊推理机->解模糊器”的过程用一个五层结构的网络来表示，见下图：

然后利用神经网络的BP算法来训练模糊系统的参数，使得误差函数J(k)=[y^*(k)-f(x^*(k)|w)]²达到最小。Roger Jang将这种网络化表示的模糊系统称作“模糊神经网络”。这篇论文在google scholar被引用20766次，标志着模糊神经网络领域的诞生。

Roger Jang（张智星）是Zadeh最后一个博士生，我1992年去Zadeh那里做博士后时Roger是读博最后一年。我和Roger在同一间办公室（Zadeh学科组学生学者的办公室）里工作了几个月。关于“模糊神经网络”的提法，我和Roger有不同的意见。我认为，模糊系统用网络形式来表示，只是一种图形化的表示方式而已，其本质还是模糊系统，与神经网络没有关系。因此，我觉得如果使用“模糊神经网络”这个名称，会让人们产生误解，以为模糊系统是神经网络的一种，而忽略了模糊系统是“基于规则的系统”（rule-based system）这个本质。Roger不同意我的观点，他认为“模糊神经网络”的提法可以将模糊系统和神经网络两大领域联系起来，具有很好的“宣传”效用。我当时对于所谓的宣传效用不以为然，所以我一直没有使用模糊神经网络这个提法。

现在，三十多年过去了，我和Roger到底谁对谁错呢？显然，Roger是对的：Roger的论文被引用两万多次，而我的论文只被引用了几百次，虽然这两篇论文都是用BP算法训练模糊系统、虽然我的论文比Roger的论文还要早发表一年。其实，即使现在，我依然觉得“模糊神经网络”的提法有误导作用：模糊系统是基于模糊规则和模糊逻辑推理的系统，具有很好的可解释性（模糊规则一环套一环），而神经网络是黑箱，两者有着完全不同的理念与技术内涵。Roger博士毕业后去了Mathworks，MATLAB中的模糊系统toolbox就是他编制的。Roger给我抱怨说，Mathworks派了一个硕士来领导他，让他很不爽。后来Roger回台大任教，主要从事音乐信号处理方面的研究工作。

  除了上面我和Roger的论文，另外一项模糊神经网络的开篇之作是Kosko的名著“神经网络与模糊系统”：

B. Kosko,“Neural Networks and Fuzzy Systems”，Prentice Hall，1992.

这本书第一次将神经网络和模糊系统放在一起来介绍与探讨，也可以看做是模糊神经网络领域的开山之作。这本书在google scholar被引用9176次。Kosko是我进入模糊领域的授课老师，他一直在南加大电机系任教，后来考了个律师执照，业余时间在洛杉矶从事律师工作。Kosko教授是个“神人”，他上课时给我们说，他的关于神经网络和模糊系统的灵感是泡在冲浪浴缸中想出来的，让我们这些学生佩服的五体投地。

四、自适应模糊控制

到1990年代初，虽然模糊控制在应用中取得了良好的效果，但当时的模糊控制器只是经验控制，性能取决于专家经验的好坏，而且不能保证最基本的稳定性、收敛性等，也不能进行优化设计。当时（1991年），在完成了模糊系统的万能逼近定理和由数据产生模糊规则的Wang-Mendel算法之后，我将研究重点放到了模糊控制。我觉得，应该将当时基于专家经验的模糊控制器作为初始控制器，在此基础上利用自适应控制方法在线调节模糊控制器的参数，来达到确保稳定性、收敛性以及最优的性能。而且，被控对象的数学模型必须是未知的，因为如果被控对象的数学模型已知，那么就应该用传统的控制方法来解决，而不应该使用模糊控制。下面简单介绍自适应模糊控制器的基本设计方法。

考虑被控对象

其中g(x)为未知非线性函数，x为被控对象的状态输出，u为控制输入。控制的目的是让x跟踪任意一条需要跟踪的曲线x^*(t)。如果g(x)是已知的，那么可以采用下面的控制器：

其中 e=x(t)-x^*(t) 为跟踪误差。将上面的控制u带入被控对象，得到

即e(t)=e^-10t，也就是说，x(t)可以很快跟踪上被跟踪曲线x^*(t)。现在的问题是g(x)未知，所以上面的控制器无法实现。自适应模糊控制的思路就是用模糊系统f(x|w)来逼近未知的g(x)，通过在线调节模糊系统f(x|w)的参数向量w，使得f(x|w)能够快速逼近g(x)。由于模糊系统f(x|w)是万能逼近器，所以可以任意逼近未知的非线性函数g(x)。用模糊系统f(x|w)代替未知的非线性函数g(x)，我们得到可实现的模糊控制器：

接下来的问题是如何在线调节模糊系统f(x|w)的参数向量w，使得x(t)能够跟踪上x^*(t)。设定Lyapunov函数V=e²+(w-w^*)²，通过dV/dt<0，我们得到w的自适应调节侓：

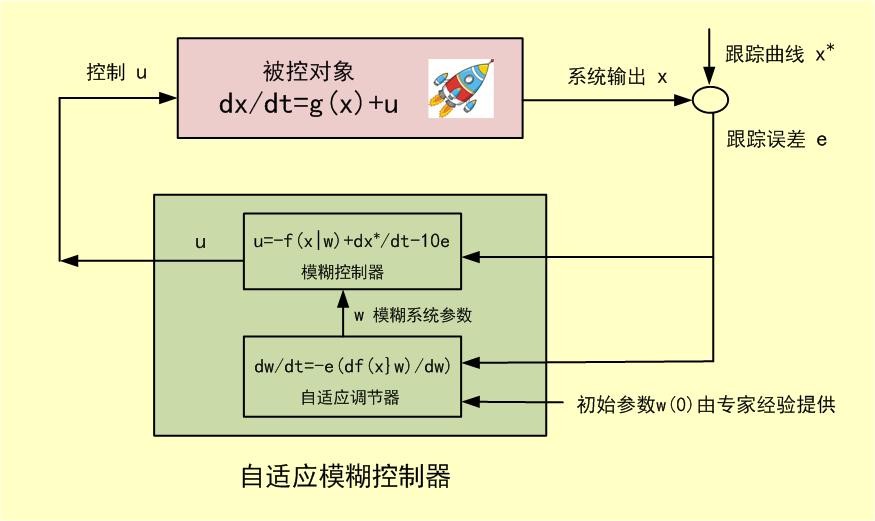
其中初始参数w(0)由专家经验提供（专家控制经验通过这种方式融入到控制系统当中）。这个自适应调节器为模糊控制器提供实时参数w(t)，两者一起构成了自适应模糊控制器，见下图：

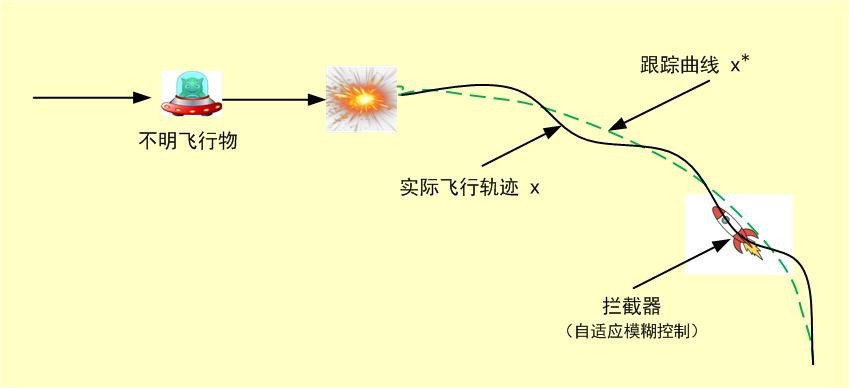
由于自适应模糊控制不需要知道被控对象的数学模型，而且被控对象可以是任意复杂的非线性时变系统，所以自适应模糊控制有着广泛的应用场景。比如，不明飞行物的拦截系统就是典型的应用，见下图：

由于拦截器燃料消耗以及环境的快速变化，无法建立精确的数学模型，而这正是自适应模糊控制适用的场景。

与其它非线性自适应控制器相比（比如基于神经网络的自适应控制器），自适应模糊控制的独特优势在于：模糊控制器的参数具有明确的物理意义，可以通过专家经验来选取，这就使得初始控制器更加接近于最优控制器。对于非线性自适应控制来讲，由于被控对象模型未知，需要边控制边学习，所以初始控制器的好坏至关重要，直接关系到整个闭环控制系统能否稳定运行。

自适应模糊控制的基本理论框架以及最基本的稳定性、收敛性、最优性定理总结于下面的研究专著：

L. X. Wang, Adaptive Fuzzy Systems and Control: Design and Stability Analysis, Prentice-Hall: Englewood Cliffs, NJ, 1994.

这本书在google scholar被引用5750次，是专注于模糊控制的学术专著之中被引用最高的。此书出版之前，人们经常批评模糊控制没有理论支撑；此书出版之后，就很少有人再这么说了，因为传统控制理论所拥有的严格理论支撑，在这本书中都有，其严谨、深刻、全面的特征不亚于任何传统的控制理论。

五、继往开来

模糊理论经过1990年代初的几年的突破性发展（万能逼近定理，模糊神经网络，自适应模糊控制等），领域呈现出继往开来的大好局面。到1990年代中期，一项重要的任务是撰写一本模糊系统与模糊控制的标准教材，承前启后，推动领域迈向新的时代。这本教材应该在传承模糊理论数学时代（1965-1990）最核心理论的基础之上，引领模糊理论进入全新的数据时代（1990-2015）。经过三年在香港科大的教学实践，我于1997年出版了这本模糊理论数据时代的标准教材“模糊系统与模糊控制教程”：

L. X. Wang, A Course in Fuzzy Systems and Control, Prentice-Hall: Englewood Cliffs, NJ, 1997.  

这本书在google scholar被引用5650次，是模糊系统与模糊控制领域最广泛使用的教材。此书有中译本，2003年由清华大学出版社出版：

山花烂漫红似火，百花争艳满园春。模糊理论的数据时代（1990-2015）是模糊理论蓬勃发展的二十五年：以数据为纽带，紧跟时代潮流，模糊理论走出了数学时代（1965-1990）的象牙塔，迈向了广泛的应用领域，在理论和应用方面都取得了长足的进步。但是，数据时代的模糊理论最大的缺点是只适用于小数据场景，不能很好的解决大数据问题。同一时期，神经网络领域向着深度模型、大模型、大数据的方向发展，并取得了突破性的进展，成就了当前的人工智能热潮。模糊理论应该向神经网络领域学习，向着深度模糊模型、网络化模糊模型、大数据的方向发展，紧跟时代潮流，开拓进取、砥砺前行，昂首迈向更加辉煌的下一个二十五年：模糊理论的计算时代（2015-2040）。