本人因眼睛视力不适，难以继续及时更新博客。但因杨六省老师之邀，之前转载过多篇杨老师关于数学方面的论述，如“杨六省：美国《数学教育研究杂志》的退稿理由让我无语”、“√2=p/q（p，q 互质）与√2=p/q（p和q全是整数）等价吗？”、“毕达哥拉斯学派设定√2不是有理数的反论题犯了混淆上位概念与下位概念的逻辑错误”、“试把“√2是非最简分数”设定为“√2不是分数”的反论题”、“偷换概念:把反论题‘√2是分数’换成‘√2是最简分数’”、“如何证明2的立方根不是有理数”、“一句简单的反问，足以揭示其证明是无效的”等。几天前，杨六省老师又寄来一篇新作——“运用孙子兵法破解《囚徒困境》”，希望借助科学网博客平台，就相关问题进行探讨，下面是杨六省老师的观点阐述，仅仅在此进行转载，欢迎数学行家对此进行点评，也可以直接与杨六省老师联系进行交流探讨。

运用孙子兵法破解《囚徒困境》

杨六省

yangls728@163.com

1. 囚徒困境的故事

囚徒困境是世界著名难题。自1950年被提出以来，70多年过去了，这个难题迄今仍未得到解决。

故事情节是这样的：有两名嫌犯A和B被警方抓获，被分别关押在不同的房间里接受警方的盘问。他们被告知：如果一人认罪，另一人不认罪，认罪者可获释，不认罪者将获刑10年；如果两人都认罪，他们将均获刑5年；如果两人都不认罪，他们将均获刑1年。为便于分析和比较，我们用下面的表格来表示上述条款。

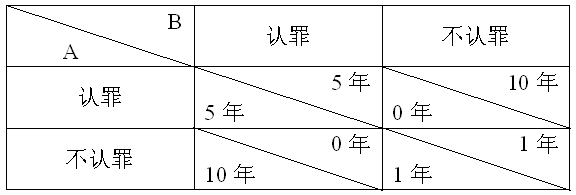
两人各会有怎样的盘算呢？

嫌犯A可能会这样想：假设B选择认罪，我若不认罪，将获刑10年，若认罪，只获刑5年，当然选择认罪有利；假设B选择不认罪，我若也不认罪，将获刑1年，我若认罪，则可获释，显然还是认罪有利。总之，不管对方选择认罪还是不认罪，认罪对我都是最佳选择。

同样，嫌犯B的盘算结果也是认为，选择认罪是最佳方案。

然而，由上述表格容易看出，两人都选择不认罪要好于两人都选择认罪，因为对前者而言，两人都只获刑1年，对后者而言，两人都获刑是5年。

上述这个与客观事实（指两个囚徒都应该选择不认罪的策略）相矛盾的推理结论（指两个囚徒都应该选择认罪的策略），就是著名的囚徒困境，也叫囚徒困境悖论。

2. 如果囚徒A不认罪，那么，囚徒B选择认罪策略是理性行为吗？

自从囚徒困境问题被提出以来，学界普遍认为，如果囚徒A选择不认罪的策略，那么，囚徒B选择认罪的策略就是一种理性行为。但是，笔者认为，这种认识是错误的，下面将给出解释。

孙子兵法曰：“知己知彼百战不殆。”意思是如果对敌我双方的情况都能了解透彻，打起仗来就不会有失败的危险。大凡每遇战事，双方事先都会进行实战推演（思想实验）。事实上，这就是双方在下一盘公开棋，不过，特别规则是可以悔棋。例如，囚徒A告诉囚徒B，他打算不认罪。B说，那我就选择认罪。这时，A说，我悔棋，我将不认罪改为认罪。这时，两人陷入反思……，最终达成共识，即两人都认罪不如两人都不认罪。于是，双方都决定悔棋，即都把认罪改为不认罪。结论是，如果囚徒A不认罪，那么，囚徒B也应该不认罪，这才是真正的理性行为——这就是中国成语所说的“大巧若拙”。

3. 两个囚徒博弈的最优解（正确答案）证明

马丁·苏比克悲观的写道（1970）：“囚徒的困境这个难题是永远也解决不了的”。

笔者一直坚信马列主义的真理观——真理是可知的。据此，笔者认为，囚徒困境是可破解的。事实上，笔者曾对两个囚徒博弈的最优解给出过三种证法（参见：杨六省著《悖论是什么——70个悖论的消解》一书，武汉，汉斯出版社，2020年），但下面的新证明是活生生的，就像两人面对面下棋一样。

证明：①假设对方选择认罪的策略，很显然，我也应该选择认罪的策略。

②假设对方选择不认罪的策略，如果我选择认罪的策略，对方会知道我的想法，并知道他将陷于最坏境地。由于做决策是同步思考的，所以，对方有权随时调整策略，也就是说，为了避免最坏情况的发生，对方必然会把原来的不认罪策略改为认罪策略——这时出现两人都认罪了。但是，我很清楚，两人都认罪不如两人都不认罪。因此，假设对方选择不认罪的策略，那么，我也应该选择不认罪的策略。

③综上所述，无论对方选择什么策略，我都应该选择与对方相同的策略。对方也会这样想。简言之，两人的策略选择应该是一致的。

④如果我选择认罪的策略，则对方也会选择认罪的策略，但这显然不是最好的方案。对方也会这样想。

⑤于是，两人将不约而同地都选择不认罪的策略。（证完）

基于上述推演，囚徒困境这一世界著名难题就得以破解.了。

说明：本文内容选自《悖论：披着羊皮的狼——对99个悖论的消解》（线装书局出版社，2023.6）。京东搜索“杨六省”即可找到该书。