博文
学三角多项式逼近和快速傅立叶变换(二)
||
5. 快速离散傅立叶变换(FFT)
因复数形式正逆变换,归结为计算 

即,N个xk的傅里叶变换转换为N/2长度的两个傅里叶变换。可依次再分割下去。如N=8个离散点时:
(x0,x1,x2,x3,x4,x5,x6,x7)划分为(x0,x2,x4,x6)(x1,,x3,x5,x7)
再划分为:((x0,x4)(x2,x6))((x1,x5),(x3,x7)),
直到(x0,x4,x2,x6,x1,x5,x3,x7)
用二进制表示下标为
(x000,x100,x010,x110,x001,x101,x011,x111)
正好是原来数字的二进制逆序。
(4) 人工计算
先算4个点,e-i2π/N的n次,n=0时w[0]为1,n=1时w[1]为-i
x[0]=0, x[0]=x[0]+x[2]*w[0]=0, x[0]=x[0]+x[1]*w[0]=0 c[0]=x[0]=0
x[1]=1, x[1]=x[1]+x[3]*w[0]=0, x[1]=x[0]-x[1]*w[0]=0 c[1]=x[2]=-2i
x[2]=0, x[2]=x[0]-x[2]*w[0]=0, x[2]=x[2]+x[3]*w[1]=-2i c[2]=x[1]=0
x[3]=-1,x[3]=x[1]-x[3]*w[0]=2, x[3]=x[2]-x[3]*w[1]=2i c[3]=x[3]=2i
或
x[0]=0, x[0]=x[0]+x[2]*w[0]=0, x[0]=x[0]+x[1]*w[0]=0 c[0]=x[0]=0
x[2]=0, / x[2]=x[0]-x[2]*w[0]=0, x[2]=x[2]+x[3]*w[1]=-2i c[2]=x[1]=0
x[1]=1, x[1]=x[1]+x[3]*w[0]=0, x[1]=x[0]-x[1]*w[0]=0 c[1]=x[2]=-2i
x[3]=-1,/ x[3]=x[1]-x[3]*w[0]=2, x[3]=x[2]-x[3]*w[1]=2i c[3]=x[3]=2i
c[k]=c[k]/N,这里N=4
A[k]=2*R(c[k]),这里为0, B[k]=-2*I(C[k]/N)
B[1]=1,即1*sin(t),t取0,π/2,π,-π/2时,采样值为0,1,0,-1
w(N,k+N/2)=-w(N,k)
(5) 二进制的逆序
int nx(int k,int p) //p为总的位数
{ int q,t=0;
for(q=0;q<p;q++)
if((1<<q)&k) //如果倒数第q位是1 (q从0起)
t+=1<<(p-q-1); //那么,正数第q位是1, 即t就累加 2的(p-q-1)次方
return t;
}
(6) FTT的C语言程序
void kj_FFT(COMPLEX *T,COMPLEX *F,int p)//20141123
{ //结合《数值分析》P89变量的定义
//p为log2(N);
int N,q,k,r,j,i,t;
// q为递推步,从0到p-1共p步
// k为每步中蝶块号,第一步0,第二步0,1
// r 为每个蝶块中元素个数之半
// j为各步每蝶块中前一半的元素号
// q 0 1 2 3
//块数 1 2 4 8
//块号k=1<<q
// r 8 4 2 1
// A的下标 j+k*2^(p-q)
COMPLEX *A1,*A2, *W;
double a;
N=1<<p;
A1=(COMPLEX *)malloc(sizeof(COMPLEX)*N);
A2=(COMPLEX *)malloc(sizeof(COMPLEX)*N);
W =(COMPLEX *)malloc(sizeof(COMPLEX)*N/2);
for(i=0;i<N;i++)
A1[i]=T[i];
for(i=0;i<N/2;i++)
{ a=-i*2*PI/N; // 正变为负,逆为正,a=i*2*PI/N;
W[i].R=cos(a);
W[i].I=sin(a);
// printf("%lf,%lf,%dn",W[i].R,W[i].I,i);
}
for(q=0;q<p;q++)
{for(k=0;k<1<<q;k++)
{ r=1<<(p-q-1);
for(j=0;j<r;j++)
{ t=k*( 1<<(p-q) );
A2[j+t] =add(A1[j+t], mul(A1[j+t+r],W[ nx((j+t)>>(p-q-1),p)]) );
A2[j+t+r]=sub(A1[j+t], mul(A1[j+t+r],W[ nx((j+t)>>(p-q-1),p)]) );
// printf("%d = %d + %d * %d|n",j+t,j+t,j+t+r, nx((j+t)>>(p-q-1),p) );
//printf("%d = %d - %d * %dn",j+t+r,j+t,j+t+r, nx((j+t)>>(p-q),p)/2 );
}
}
for(i=0;i<N;i++)
A1[i]=A2[i];
//printf("n");
}
for(i=0;i<N;i++)
{
F[i].R=A2[nx(i,p)].R/N; //正变换除以N,逆变换不用除
F[i].I=A2[nx(i,p)].I/N;
printf("F%d =A%dn",i,nx(i,p));
}
}
分析算法结合以下图示,8个点
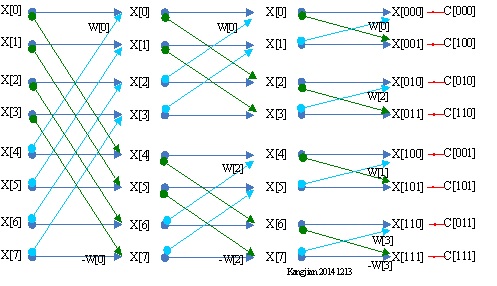

16个点

6. 应用示例
(0)先写一段函数绘图及区间变换程序,以便演示应用
#include <stdio.h>
#include <graphics.h>
#include <conio.h>
#include <math.h>
int draw(double x[],double y[],int n)
{
if(n>1)
{
int W=600,H=600;//1024,768
int margin=20;
initgraph(W, H); // easyX C
setbkcolor(RGB(255,255,255));
cleardevice();
setcolor(RGB(255,0,0) );
W=W-2*margin;H=H-2*margin;
int i,*X;
X=(int *)malloc(n*sizeof(int)); //c
int *Y=new int[n]; //c++
double min_x,max_x,min_y,max_y;
min_x=max_x=x[0];
min_y=max_y=y[0];
for(i=1;i<n;i++)
{
if(x[i]<min_x) min_x=x[i];
if(x[i]>max_x) max_x=x[i];
if(y[i]<min_y) min_y=y[i];
if(y[i]>max_y) max_y=y[i];
}
for(i=0;i<n;i++)
{
X[i]=margin+ (int)( (x[i] -min_x)/ (max_x-min_x) * W );
Y[i]=margin+H-(int)( (y[i] -min_y)/ (max_y-min_y) * H );
}
moveto(X[0],Y[0]);
for(i=1;i<n;i++)
{ lineto(X[i],Y[i]);
}
char s[50];
sprintf(s,"%f,%f",x[0],y[0]);
outtextxy(X[0],Y[0],s);
//printf("|x|/|y|=%lfn",(max_x-min_x)/(max_y-min_y));
getch();
closegraph();
return 1;
}
else
{ return 0;}
}
void DrawFunction(double (*f)(double x),double a,double b)
{ int n=100,i;
double h;
double *x=new double[n];
double *y=new double[n];
h=(b-a)/n;
for(i=0;i<n;i++){
x[i]=a;
y[i]=f(x[i]);
a+=h;
}
draw(x,y,n);
}
double fs(double x)
{
return 2*sin(x);
}
void main()
{
DrawFunction(fs,-13,10);
}
对于区间变换:
(1) 三角多项式逼近
验证手工计算
void main()
{ int n=4;
COMPLEX *pT,*pF;
pT=(COMPLEX *)malloc(sizeof(COMPLEX)*n);
pF=(COMPLEX *)malloc(sizeof(COMPLEX)*n);
pT[0].R=0;pT[0].I=0;
pT[1].R=1;pT[1].I=0;
pT[2].R=0;pT[2].I=0;
pT[3].R=-1;pT[3].I=0;
//kj_DFT(pT,pF,n);
kj_FFT(pT,pF,2);
for(int k=0;k<n;k++) //Ck=>Ak,Bk
{ pF[k].R=2*pF[k].R;
pF[k].I=-2*pF[k].I;
printf("%lf, %lf, k=%dn", pF[k].R, pF[k].I, k);
}
}
输出为:
0 = 0 + 2 * 0
2 = 0 - 2 * 0
1 = 1 + 3 * 0
3 = 1 - 3 * 0
0 = 0 + 1 * 0
1 = 0 - 1 * 0
2 = 2 + 3 * 1
3 = 2 - 3 * 1
F0 =A0
F1 =A2
F2 =A1
F3 =A3
0.000000, 0.000000, k=0
0.000000, 1.000000, k=1
0.000000, 0.000000, k=2
-0.000000, -1.000000, k=3
若pT[].R都为1,输出:2.0000,0.00000,k=0,其它值为0
page90-91,例13
double f1(double x)
{ return x*x*x*x-3*x*x*x+2*x*x-tan(x*(x-2));
}
void main()
{ int n=8,j,k;
COMPLEX *pT,*pF,*pTT;
double t=1;
pT=(COMPLEX *)malloc(sizeof(COMPLEX)*n);
pF=(COMPLEX *)malloc(sizeof(COMPLEX)*n);
double bj_a=0,bj_b=2;
for(j=0;j<n;j++) //采样
{ pT[j].R=f1(bj_a+j*(bj_b-bj_a)/n);
pT[j].I=0.;
}
kj_FFT(pT,pF,3);//kj_DFT(pT,pF,n);
for(k=0;k<n;k++) //Ck=>Ak,Bk
{ pF[k].R=2*pF[k].R;
pF[k].I=-2*pF[k].I;
printf("%lf, %lf, k=%dn", pF[k].R, pF[k].I, k);
}
double S=0,tx,ty;
for(tx=bj_a;tx<=bj_b;tx+=0.05)
{ ty=PI*tx;//y=c+(d-c)/(b-a)*(x-a), 由[0,2pi]转换到[0,2]
S=pF[0].R/2; //A[0]/2
for(j=1;j<=n/2-1;j++)
S+=pF[j].R*cos(j*ty)+pF[j].I*sin(j*ty);
S+=pF[j].R*cos(j*ty)/2; //A[n/2]/2
printf("%lf,%lf,------%lfn",tx,S, S-f1(tx));
}
}
输出为:
0 = 0 + 4 * 0
4 = 0 - 4 * 0
1 = 1 + 5 * 0
5 = 1 - 5 * 0
2 = 2 + 6 * 0
6 = 2 - 6 * 0
3 = 3 + 7 * 0
7 = 3 - 7 * 0
0 = 0 + 2 * 0
2 = 0 - 2 * 0
1 = 1 + 3 * 0
3 = 1 - 3 * 0
4 = 4 + 6 * 2
6 = 4 - 6 * 2
5 = 5 + 7 * 2
7 = 5 - 7 * 2
0 = 0 + 1 * 0
1 = 0 - 1 * 0
2 = 2 + 3 * 2
3 = 2 - 3 * 2
4 = 4 + 5 * 1
5 = 4 - 5 * 1
6 = 6 + 7 * 3
7 = 6 - 7 * 3
F0 =A0
F1 =A4
F2 =A2
F3 =A6
F4 =A1
F5 =A5
F6 =A3
F7 =A7
1.523957, 0.000000, k=0
-0.771841, 0.386374, k=1
0.017304, 0.046875, k=2
-0.006863, 0.011374, k=3
-0.001157, 0.000000, k=4
-0.006863, -0.011374, k=5
0.017304, -0.046875, k=6
-0.771841, -0.386374, k=7
0.000000,0.000000,------0.000000
0.050000,0.089605,-------0.012836
0.100000,0.193851,-------0.015569
0.150000,0.308106,-------0.012125
0.200000,0.427985,-------0.006018
0.250000,0.549761,-------0.000000
0.300000,0.670629,------0.004170
0.350000,0.788762,---.....
可用Matlab或C语言绘图
double f2(double x)
{
return 3*cos(x)+4*cos(2*x)+5*cos(3*x)+5*sin(2*x)-0.8*sin(3*x)+2.5*sin(4*x)
+15*cos(15*x); //若N=32,显然频率大于15就不准。
//以上取0到2*PI拟合的很好
//return x>0?x:-x;
}
void test3()
{
int n=32,j,k;
COMPLEX *pT,*pF;
pT=(COMPLEX *)malloc(sizeof(COMPLEX)*n);
pF=(COMPLEX *)malloc(sizeof(COMPLEX)*n);
double bj_a=0,bj_b=2*PI;
for(j=0;j<n;j++)
{
pT[j].R=f2(bj_a+j*(bj_b-bj_a)/n); //
pT[j].I=0.;
}
//n=4;
// kj_DFT(pT,pF,n);
kj_FFT(pT,pF,5);//
for(k=0;k<=n;k++)//
{
pF[k].R=pF[k].R*2;// 2/n 同6.4式
pF[k].I=pF[k].I*2;
printf("%lf,,%lf, k=%dn", pF[k].R, pF[k].I, k);
}
FILE *fp;
if((fp=fopen("out1.txt","w"))==NULL)
{printf("file ,error!n"); exit(0) ;
}
double S,xx;
for(xx=bj_a;xx<=bj_b;xx+=0.01)
{
S=pF[0].R/2;
for(j=1;j<=n/2-1;j++)
S+=pF[j].R*cos(j*xx)-pF[j].I*sin(j*xx);//这里sin前取负号,共轭才对
S=S+1/2*pF[n/2].R*cos(n/2*xx);//这时的区间也是[2,2*PI]
// printf("%lf,%lfn",xx,S);
fprintf(fp,"%lf,%lf, %lf, %lfn",xx,S,f2(xx),S-f2(xx));
}
}
void main()
{
test1();
//test2();
//test2_1();
// test3();
}
函数逼近图示


(2) 数字滤波
// X=[5,32,38,-33,-19,-10,1,-8,-20,10,-1,4,11,-1,-7,-2]';fft(X,n)
void test1()
{ int n=16,k;
COMPLEX *pT,*pF,*pTT;
pT=(COMPLEX *)malloc(sizeof(COMPLEX)*n);
pF=(COMPLEX *)malloc(sizeof(COMPLEX)*n);
pTT=(COMPLEX *)malloc(sizeof(COMPLEX)*n);
pT[0].R=5. ; pT[0].I= 0 ;
pT[1].R=32. ; pT[1].I= 0 ;
.....
pT[14].R= -7 ; pT[14].I= 0 ;
pT[15].R=-2 ; pT[15].I= 0 ;
//n=4;
// kj_DFT(pT,pF,n);
kj_FFT(pT,pF,4);
for(k=0;k<n;k++)
{
printf("%lf,,%lf, k=%dn", pF[k].R, pF[k].I, k);
}
kj_FFT_V(pF,pTT,4);
for(k=0;k<n;k++)
{
printf("%lf,%lf, k=%dn", pTT[k].R, pTT[k].I, k);
}
}
https://blog.sciencenet.cn/blog-797552-880854.html
上一篇:学三角多项式逼近和快速傅立叶变换(一)
下一篇:亻谷
全部作者的精选博文
- • 北京胡同(三)天空和树影
- • 地球物理公式墙